EIGENSCHAFTEN VON FUNKTIONEN, DIE IN EINEM INTERVIEW KONTINUIERLICH SIND

Betrachten wir einige Eigenschaften von Funktionen, die in einem Intervall stetig sind. Wir präsentieren diese Eigenschaften ohne Beweis.

Funktion y = f(x) angerufen kontinuierlich auf dem Segment [A, B], wenn es an allen inneren Punkten dieses Segments und an seinen Enden stetig ist, d.h. an Punkten A Und B, ist rechts bzw. links stetig.

Satz 1. Eine auf dem Intervall [ stetige Funktion A, B], nimmt mindestens an einer Stelle dieses Segments den größten Wert und an mindestens einer Stelle den kleinsten an.

Der Satz besagt, dass wenn eine Funktion y = f(x) ist stetig im Intervall [ A, B], dann gibt es mindestens einen Punkt x 1 Î [ A, B], so dass der Wert der Funktion f(x) Zu diesem Zeitpunkt wird der größte aller Werte in diesem Segment sein: f(x 1) ≥ f(x). Ebenso gibt es einen solchen Punkt x 2, wobei der Funktionswert der kleinste aller Werte im Segment ist: f(x 1) ≤ f(x).

Es ist klar, dass es mehrere solcher Punkte geben kann; die Abbildung zeigt beispielsweise, dass die Funktion f(x) nimmt an zwei Punkten den kleinsten Wert an x 2 Und X 2 ".

Kommentar. Die Aussage des Theorems kann falsch werden, wenn wir den Wert der Funktion im Intervall ( A, B). In der Tat, wenn wir die Funktion betrachten y = x auf (0, 2), dann ist es in diesem Intervall stetig, erreicht aber weder den größten noch den kleinsten Wert darin: Es erreicht diese Werte an den Enden des Intervalls, aber die Enden gehören nicht dazu zu unserer Domain.

Außerdem gilt der Satz nicht mehr für diskontinuierliche Funktionen. Gib ein Beispiel.

Folge. Wenn die Funktion f(x) ist kontinuierlich auf [ A, B], dann ist es auf dieses Segment beschränkt.

Satz 2. Lassen Sie die Funktion y = f(x) ist stetig im Intervall [ A, B] und an den Enden dieses Segments Werte mit unterschiedlichen Vorzeichen annimmt, dann gibt es mindestens einen Punkt innerhalb des Segments x = C, in dem die Funktion gegen Null geht: f(C)= 0, wobei a< C< b

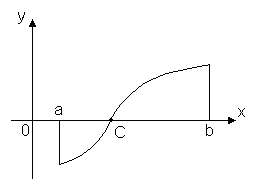
Dieser Satz hat eine einfache geometrische Bedeutung: wenn die Punkte des Graphen einer stetigen Funktion y = f(x), entsprechend den Enden des Segments [ A, B] liegen auf gegenüberliegenden Seiten der Achse Ochse, dann schneidet dieser Graph die Achse an mindestens einem Punkt des Segments Ochse. Diskontinuierliche Funktionen verfügen möglicherweise nicht über diese Eigenschaft.

Dieser Satz lässt die folgende Verallgemeinerung zu.

Satz 3 (Zwischenwertsatz). Lassen Sie die Funktion y = f(x) ist stetig im Intervall [ A, B] Und f(a) = A, f(b) = B. Dann für eine beliebige Zahl C, abgeschlossen zwischen A Und B, es gibt einen solchen Punkt innerhalb dieses Segments CÎ [ A, B], Was f(c) = C.

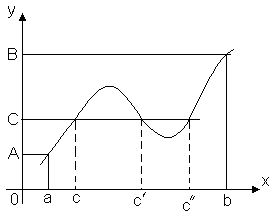
Dieser Satz ist geometrisch offensichtlich. Betrachten Sie den Graphen der Funktion y = f(x). Lassen f(a) = A, f(b) = B. Dann jede gerade Linie y = C, Wo C– eine beliebige Zahl dazwischen A Und B, schneidet den Graphen der Funktion mindestens an einem Punkt. Die Abszisse des Schnittpunkts ist dieser Wert x = C, bei welchem f(c) = C.

Somit durchläuft eine stetige Funktion, die sich von einem Wert zum anderen bewegt, notwendigerweise alle Zwischenwerte. Insbesondere:

Folge. Wenn die Funktion y = f(x)über ein bestimmtes Intervall kontinuierlich ist und die größten und kleinsten Werte annimmt, nimmt es in diesem Intervall mindestens einmal jeden Wert an, der zwischen seinen kleinsten und größten Werten liegt.

Derivat und seine Anwendungen. DEFINITION VON Derivat

Lassen Sie uns eine Funktion haben y=f(x), in einem bestimmten Intervall definiert. Für jeden Argumentwert X aus diesem Intervall die Funktion y=f(x) hat eine bestimmte Bedeutung.

Betrachten Sie zwei Argumentwerte: initial X 0 und neu X.

Unterschied x–x 0 heißt durch Inkrementieren des Arguments x am Punkt X 0 und wird bezeichnet Δx. Auf diese Weise, Δx = x – x 0 (das Argumentinkrement kann entweder positiv oder negativ sein). Aus dieser Gleichheit folgt das x=x 0 +Δx, d.h. Der Anfangswert der Variablen wurde etwas erhöht. Dann, wenn an der Stelle X 0 Funktionswert war f(x 0 ), dann an einem neuen Punkt X Die Funktion übernimmt den Wert f(x) = f(x 0 +Δx).

Unterschied j–j 0 = f(x) – f(x 0 ) angerufen Funktionsinkrement y = f(x) am Punkt X 0 und wird durch das Symbol angezeigt Δy. Auf diese Weise,

Normalerweise der Anfangswert des Arguments X 0 gilt als fest und der neue Wert X– variabel. Dann j 0 = f(x 0 ) stellt sich als konstant heraus und y = f(x)– variabel. Schritte Δy Und Δx werden auch Variablen sein und Formel (1) zeigt das Dy ist eine Funktion einer Variablen Δx.

Erstellen wir das Verhältnis des Inkrements der Funktion zum Inkrement des Arguments

Finden wir die Grenze dieses Verhältnisses bei Δx→0. Wenn dieser Grenzwert existiert, wird er als Ableitung dieser Funktion bezeichnet f(x) am Punkt X 0 und bezeichnen F "(X 0). Also,

Derivat diese Funktion y = f(x) am Punkt X 0 wird als Grenze des Funktionsinkrementverhältnisses Δ bezeichnet j zum Argumentinkrement Δ X, wenn letzterer willkürlich gegen Null tendiert.

Beachten Sie, dass für dieselbe Funktion die Ableitung an verschiedenen Punkten erfolgt X kann unterschiedliche Werte annehmen, d.h. Die Ableitung kann als Funktion des Arguments betrachtet werden X. Diese Funktion ist gekennzeichnet F "(X)

Die Ableitung wird durch die Symbole bezeichnet F "(x),y", . Der spezifische Wert der Ableitung bei x = ein bezeichnet durch F "(A) oder j "| x=a.

Die Operation, die Ableitung einer Funktion zu finden f(x) heißt Differentiation dieser Funktion.

Um die Ableitung per Definition direkt zu finden, können Sie Folgendes verwenden: Faustregel:

Beispiele.

MECHANISCHER Sinn für Ableitung

Aus der Physik ist bekannt, dass das Gesetz der gleichförmigen Bewegung die Form hat s = v t, Wo S– der zurückgelegte Weg zum Augenblick der Zeit T, v– Geschwindigkeit der gleichförmigen Bewegung.

Allerdings, weil Die meisten Bewegungen in der Natur sind ungleichmäßig, daher im Allgemeinen die Geschwindigkeit und damit auch die Entfernung S wird von der Zeit abhängen T, d.h. wird eine Funktion der Zeit sein.

Lassen Sie also einen materiellen Punkt gemäß dem Gesetz geradlinig in eine Richtung bewegen s=s(t).

Markieren wir einen bestimmten Zeitpunkt T 0 . An diesem Punkt hat der Punkt den Pfad überschritten s=s(t 0 ). Bestimmen wir die Geschwindigkeit v materieller Punkt zu einem bestimmten Zeitpunkt T 0 .

Betrachten wir dazu einen anderen Zeitpunkt T 0 + Δ T. Sie entspricht dem zurückgelegten Weg s =s(t 0 + Δ T). Dann über einen Zeitraum Δ T der Punkt hat den Weg Δs zurückgelegt =s(t 0 + Δ T)–s(t).

Betrachten wir die Einstellung. Sie wird als Durchschnittsgeschwindigkeit im Zeitintervall Δ bezeichnet T. Die Durchschnittsgeschwindigkeit kann die aktuelle Bewegungsgeschwindigkeit eines Punktes nicht genau charakterisieren T 0 (weil die Bewegung ungleichmäßig ist). Um diese wahre Geschwindigkeit anhand der Durchschnittsgeschwindigkeit genauer auszudrücken, müssen Sie eine kürzere Zeitspanne Δ verwenden T.

Also die Bewegungsgeschwindigkeit zu einem bestimmten Zeitpunkt T 0 (Momentangeschwindigkeit) ist die Grenze der Durchschnittsgeschwindigkeit im Intervall von T 0 bis T 0 +Δ T, wenn Δ T→0:

,

diese. ungleichmäßige Geschwindigkeit Dies ist die Ableitung der zurückgelegten Strecke nach der Zeit.

GEOMETRISCHE BEDEUTUNG DES Derivats

Lassen Sie uns zunächst die Definition einer Tangente an eine Kurve an einem bestimmten Punkt einführen.

Lassen Sie uns eine Kurve und einen Fixpunkt darauf haben M 0(siehe Abbildung). Betrachten Sie einen anderen Punkt M diese Kurve und zeichne eine Sekante M 0 M. Wenn der Punkt M beginnt sich entlang der Kurve und des Punktes zu bewegen M 0 bleibt bewegungslos, dann ändert die Sekante ihre Position. Wenn, mit unbegrenzter Annäherung an den Punkt M entlang einer Kurve zu einem Punkt M 0 Auf jeder Seite neigt die Sekante dazu, die Position einer bestimmten geraden Linie einzunehmen M 0 T, dann gerade M 0 T wird als Tangente an die Kurve an einem bestimmten Punkt bezeichnet M 0.

Das., Tangente zur Kurve an einem bestimmten Punkt M 0 wird als Grenzposition der Sekante bezeichnet M 0 M wenn Punkt M tendiert entlang der Kurve zu einem Punkt M 0.

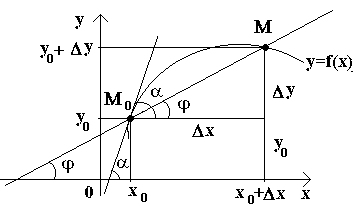
Betrachten wir nun die stetige Funktion y=f(x) und die dieser Funktion entsprechende Kurve. Zu einem gewissen Wert X 0-Funktion nimmt Wert an y 0 =f(x 0). Diese Werte X 0 und j 0 auf der Kurve entspricht einem Punkt M 0 (x 0 ; y 0). Lassen Sie uns das Argument vorbringen x 0 Inkrement Δ X. Der neue Wert des Arguments entspricht dem inkrementierten Wert der Funktion j 0 +Δ y=f(x 0 –Δ X). Wir haben es verstanden M(x 0+Δ X; y 0+Δ y). Zeichnen wir eine Sekante M 0 M und bezeichnen mit φ den Winkel, den eine Sekante mit der positiven Richtung der Achse bildet Ochse. Lassen Sie uns eine Beziehung erstellen und das bemerken.

Wenn nun Δ X→0, dann aufgrund der Stetigkeit der Funktion Δ bei→0 und damit der Punkt M, bewegt sich entlang einer Kurve und nähert sich dem Punkt unbegrenzt M 0. Dann die Sekante M 0 M neigt dazu, die Position einer Tangente an die Kurve an dem Punkt einzunehmen M 0, und der Winkel φ→α bei Δ X→0, wobei α den Winkel zwischen der Tangente und der positiven Richtung der Achse bezeichnet Ochse. Da die Funktion tan φ für φ≠π/2 kontinuierlich von φ abhängt, ist für φ→α tan φ → tan α und daher die Steigung der Tangente:

diese. f "(x)= tg α .

Also geometrisch y "(x 0) stellt die Steigung der Tangente an den Graphen dieser Funktion am Punkt dar x 0, d.h. für einen gegebenen Argumentwert X, die Ableitung ist gleich dem Tangens des Winkels, den die Tangente an den Funktionsgraphen bildet f(x) an der entsprechenden Stelle M 0 (x; y) mit positiver Achsrichtung Ochse.

Beispiel. Finden Sie die Steigung der Tangente an die Kurve y = x 2 am Punkt M(-1; 1).

Wir haben bereits früher gesehen, dass ( X 2)" = 2X. Der Winkelkoeffizient der Tangente an die Kurve beträgt jedoch tan α = j"| x=-1 = – 2.

DIFFERENZIERBARKEIT DER FUNKTIONEN. Kontinuität der differenzierbaren Funktion

Funktion y=f(x) angerufen differenzierbar Irgendwann X 0, wenn es an dieser Stelle eine bestimmte Ableitung hat, d.h. wenn die Grenze der Beziehung existiert und endlich ist.

Wenn eine Funktion an jedem Punkt eines bestimmten Segments differenzierbar ist [ A; B] oder Intervall ( A; B), dann sagen sie, dass sie differenzierbar auf dem Segment [ A; B] bzw. im Intervall ( A; B).

Es gilt der folgende Satz, der den Zusammenhang zwischen differenzierbaren und stetigen Funktionen herstellt.

Satz. Wenn die Funktion y=f(x) irgendwann differenzierbar x 0, dann ist es an dieser Stelle stetig.

Aus der Differenzierbarkeit einer Funktion folgt also ihre Stetigkeit.

Nachweisen. Wenn , Das

,

wobei α eine unendlich kleine Größe ist, d.h. eine Größe, die als Δ gegen Null geht X→0. Aber dann

Δ j=F "(x 0) Δ X+αΔ X=> Δ j→0 bei Δ X→0, d.h. f(x) – f(x 0)→0 um X→X 0 , was bedeutet, dass die Funktion f(x) kontinuierlich an einem Punkt X 0 . Q.E.D.

Daher kann die Funktion an Unstetigkeitspunkten keine Ableitung haben. Das Gegenteil ist nicht der Fall: Es gibt stetige Funktionen, die an einigen Punkten nicht differenzierbar sind (d. h. an diesen Punkten keine Ableitung haben).

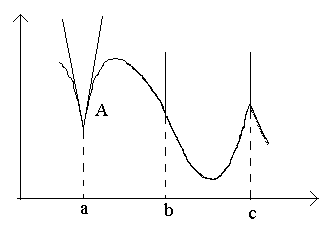
Betrachten Sie die Punkte in der Abbildung a, b, c.

Am Punkt A bei Δ X→0 hat das Verhältnis keine Grenze (da die einseitigen Grenzen für Δ unterschiedlich sind). X→0–0 und Δ X→0+0). Am Punkt A Im Diagramm gibt es keine definierte Tangente, aber es gibt zwei verschiedene Einwegtangenten mit Steigungen Zu 1 und Zu 2. Diese Art von Punkt wird Eckpunkt genannt.

Am Punkt B bei Δ X Das Verhältnis →0 ist eine vorzeichenkonstante unendlich große Größe. Die Funktion hat eine unendliche Ableitung. An diesem Punkt hat der Graph eine vertikale Tangente. Punkttyp – „Wendepunkt“ einer vertikalen Tangente.

Am Punkt C einseitige Ableitungen sind unendlich große Mengen unterschiedlicher Vorzeichen. An diesem Punkt weist der Graph zwei verschmolzene vertikale Tangenten auf. Typ – „Rückkehrpunkt“ mit vertikaler Tangente – ein Sonderfall eines Eckpunkts.

Die folgenden Abbildungen zeigen, wo die Funktion ihren kleinsten und größten Wert erreichen kann. In der linken Abbildung sind die kleinsten und größten Werte an den Punkten des lokalen Minimums und Maximums der Funktion fixiert. Im rechten Bild - an den Enden des Segments.

Wenn die Funktion j = F(X) ist stetig im Intervall [ A, B] , dann erreicht es dieses Segment am wenigsten Und höchste Werte . Dies kann, wie bereits erwähnt, in beiden Fällen passieren Extrempunkte oder an den Enden des Segments. Daher zu finden am wenigsten Und die größten Werte der Funktion , kontinuierlich im Intervall [ A, B] , müssen Sie seine Werte insgesamt berechnen kritische Punkte und an den Enden des Segments, und wählen Sie dann das kleinste und größte davon aus.

Angenommen, Sie möchten den größten Wert der Funktion ermitteln F(X) auf dem Segment [ A, B] . Dazu müssen Sie alle kritischen Punkte finden, die auf [ A, B] .

Kritischer Punkt nennt man den Punkt, an dem Funktion definiert, und sie Derivat entweder gleich Null oder nicht vorhanden. Dann sollten Sie die Werte der Funktion an den kritischen Punkten berechnen. Und schließlich sollte man die Werte der Funktion an kritischen Punkten und an den Enden des Segments vergleichen ( F(A) Und F(B)). Die größte dieser Zahlen wird sein der größte Wert der Funktion im Segment [A, B] .

Probleme beim Finden kleinste Funktionswerte .

Wir suchen gemeinsam nach dem kleinsten und größten Wert der Funktion

Beispiel 1. Finden Sie den kleinsten und größten Wert einer Funktion auf dem Segment [-1, 2] .

Lösung. Finden Sie die Ableitung dieser Funktion. Setzen wir die Ableitung mit Null () gleich und erhalten zwei kritische Punkte: und . Um die kleinsten und größten Werte einer Funktion auf einem bestimmten Segment zu finden, reicht es aus, ihre Werte an den Enden des Segments und am Punkt zu berechnen, da der Punkt nicht zum Segment gehört [-1, 2]. Diese Funktionswerte sind: , , . Es folgt dem kleinster Funktionswert(im Diagramm unten rot angezeigt), gleich -7, wird am rechten Ende des Segments erreicht - am Punkt , und größte(in der Grafik ebenfalls rot), beträgt am kritischen Punkt 9,-.

Wenn eine Funktion in einem bestimmten Intervall stetig ist und dieses Intervall kein Segment ist (sondern z. B. ein Intervall ist); der Unterschied zwischen einem Intervall und einem Segment: Die Randpunkte des Intervalls sind nicht im Intervall enthalten, sondern die Randpunkte des Segments sind im Segment enthalten), dann darf es unter den Werten der Funktion nicht den kleinsten und den größten geben. So ist beispielsweise die in der Abbildung unten gezeigte Funktion stetig auf ]-∞, +∞[ und hat nicht den größten Wert.

Für jedes Intervall (geschlossen, offen oder unendlich) gilt jedoch die folgende Eigenschaft stetiger Funktionen.

Zur Selbstkontrolle bei Berechnungen können Sie verwenden Online-Ableitungsrechner .

Beispiel 4. Finden Sie den kleinsten und größten Wert einer Funktion auf dem Segment [-1, 3] .

Lösung. Die Ableitung dieser Funktion finden wir als Ableitung des Quotienten:

.

Wir setzen die Ableitung mit Null gleich, was uns einen kritischen Punkt gibt: . Es gehört zum Segment [-1, 3] . Um die kleinsten und größten Werte einer Funktion auf einem bestimmten Segment zu finden, ermitteln wir ihre Werte an den Enden des Segments und am gefundenen kritischen Punkt:

Vergleichen wir diese Werte. Fazit: gleich -5/13, an Punkt und Höchster Wert gleich 1 am Punkt .

Wir suchen weiterhin gemeinsam nach den kleinsten und größten Werten der Funktion

Es gibt Lehrer, die den Schülern beim Thema Finden der kleinsten und größten Werte einer Funktion keine Lösungsbeispiele geben, die komplexer sind als die gerade besprochenen, also solche, bei denen die Funktion ein Polynom oder a ist Bruch, dessen Zähler und Nenner Polynome sind. Aber wir werden uns nicht auf solche Beispiele beschränken, denn unter den Lehrern gibt es solche, die die Schüler gerne zum vollständigen Denken zwingen (die Ableitungstabelle). Daher werden der Logarithmus und die trigonometrische Funktion verwendet.

Beispiel 8. Finden Sie den kleinsten und größten Wert einer Funktion auf dem Segment .

Lösung. Wir finden die Ableitung dieser Funktion als Derivat des Produkts :

Wir setzen die Ableitung mit Null gleich, was einen kritischen Punkt ergibt: . Es gehört zum Segment. Um die kleinsten und größten Werte einer Funktion auf einem bestimmten Segment zu finden, ermitteln wir ihre Werte an den Enden des Segments und am gefundenen kritischen Punkt:

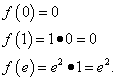
Ergebnis aller Aktionen: Die Funktion erreicht ihren Minimalwert, gleich 0, am Punkt und am Punkt und Höchster Wert, gleich e², an der Stelle.

Zur Selbstkontrolle bei Berechnungen können Sie verwenden Online-Ableitungsrechner .

Beispiel 9. Finden Sie den kleinsten und größten Wert einer Funktion auf dem Segment .

Lösung. Finden Sie die Ableitung dieser Funktion:

Wir setzen die Ableitung mit Null gleich:

Der einzige kritische Punkt betrifft das Segment. Um die kleinsten und größten Werte einer Funktion auf einem bestimmten Segment zu finden, ermitteln wir ihre Werte an den Enden des Segments und am gefundenen kritischen Punkt:

Abschluss: Die Funktion erreicht ihren Minimalwert, gleich , am Punkt und Höchster Wert, gleich , an der Stelle .

Bei angewandten Extremalproblemen kommt es beim Finden der kleinsten (maximalen) Werte einer Funktion in der Regel darauf an, das Minimum (Maximum) zu finden. Aber nicht die Minima oder Maxima selbst sind von größerem praktischen Interesse, sondern die Werte des Arguments, bei denen sie erreicht werden. Bei der Lösung angewandter Probleme entsteht eine zusätzliche Schwierigkeit: das Zusammenstellen von Funktionen, die das betrachtete Phänomen oder den betrachteten Prozess beschreiben.

Beispiel 10. Ein Tank mit einem Fassungsvermögen von 4 Litern, der die Form eines Parallelepipeds mit quadratischer Grundfläche hat und oben offen ist, muss verzinnt sein. Welche Größe sollte der Tank haben, damit möglichst wenig Material zur Abdeckung verbraucht wird?

Lösung. Lassen X- Basisseite, H- Tankhöhe, S- seine unbedeckte Oberfläche, V- seine Lautstärke. Die Oberfläche des Tanks wird durch die Formel ausgedrückt, d.h. ist eine Funktion zweier Variablen. Ausdrücken S Als Funktion einer Variablen nutzen wir die Tatsache, dass , von wo . Ersetzen des gefundenen Ausdrucks H in die Formel für S:

Lassen Sie uns diese Funktion bis zum Äußersten untersuchen. Es ist überall in ]0, +∞[ , und definiert und differenzierbar

.

Wir setzen die Ableitung mit Null () gleich und finden den kritischen Punkt. Wenn die Ableitung nicht existiert, ist dieser Wert außerdem nicht im Definitionsbereich enthalten und kann daher kein Extrempunkt sein. Das ist also der einzige kritische Punkt. Überprüfen wir anhand des zweiten ausreichenden Zeichens, ob ein Extremum vorliegt. Finden wir die zweite Ableitung. Wenn die zweite Ableitung größer als Null ist (). Dies bedeutet, dass die Funktion ein Minimum erreicht . Seit dem Minimum ist das einzige Extremum dieser Funktion, es ist ihr kleinster Wert. Die Seitenlänge des Tankbodens sollte also 2 m und seine Höhe 2 m betragen.

Zur Selbstkontrolle bei Berechnungen können Sie verwenden

Aus praktischer Sicht besteht das größte Interesse darin, mithilfe der Ableitung den größten und kleinsten Wert einer Funktion zu ermitteln. Womit hängt das zusammen? Gewinne maximieren, Kosten minimieren, optimale Auslastung der Ausrüstung ermitteln... Mit anderen Worten, in vielen Lebensbereichen müssen wir Probleme der Optimierung einiger Parameter lösen. Und das sind die Aufgaben, den größten und kleinsten Wert einer Funktion zu finden.

Es ist zu beachten, dass der größte und kleinste Wert einer Funktion normalerweise in einem bestimmten Intervall X gesucht wird, das entweder der gesamte Funktionsbereich oder ein Teil des Definitionsbereichs ist. Das Intervall X selbst kann ein Segment, ein offenes Intervall sein , ein unendliches Intervall.

In diesem Artikel werden wir darüber sprechen, den größten und kleinsten Wert einer explizit definierten Funktion einer Variablen y=f(x) zu finden.

Seitennavigation.

Der größte und kleinste Wert einer Funktion – Definitionen, Illustrationen.

Schauen wir uns kurz die wichtigsten Definitionen an.

Der größte Wert der Funktion das für jeden Ungleichheit ist wahr.

Der kleinste Wert der Funktion y=f(x) im Intervall X nennt man einen solchen Wert das für jeden Ungleichheit ist wahr.

Diese Definitionen sind intuitiv: Der größte (kleinste) Wert einer Funktion ist der größte (kleinste) akzeptierte Wert des betrachteten Intervalls auf der Abszisse.

Stationäre Punkte– Dies sind die Werte des Arguments, bei denen die Ableitung der Funktion Null wird.

Warum brauchen wir stationäre Punkte, um die größten und kleinsten Werte zu finden? Die Antwort auf diese Frage gibt der Satz von Fermat. Aus diesem Satz folgt, dass, wenn eine differenzierbare Funktion an einem Punkt ein Extremum (lokales Minimum oder lokales Maximum) hat, dieser Punkt stationär ist. Daher nimmt die Funktion häufig ihren größten (kleinsten) Wert im Intervall X an einem der stationären Punkte aus diesem Intervall an.

Außerdem kann eine Funktion ihren größten und kleinsten Wert oft an Punkten annehmen, an denen die erste Ableitung dieser Funktion nicht existiert und die Funktion selbst definiert ist.

Beantworten wir gleich eine der häufigsten Fragen zu diesem Thema: „Ist es immer möglich, den größten (kleinsten) Wert einer Funktion zu bestimmen“? Nein nicht immer. Manchmal fallen die Grenzen des Intervalls X mit den Grenzen des Definitionsbereichs der Funktion zusammen, oder das Intervall X ist unendlich. Und einige Funktionen im Unendlichen und an den Grenzen des Definitionsbereichs können sowohl unendlich große als auch unendlich kleine Werte annehmen. Über den größten und kleinsten Wert der Funktion kann in diesen Fällen keine Aussage gemacht werden.

Zur Verdeutlichung geben wir eine grafische Darstellung. Schauen Sie sich die Bilder an und vieles wird klarer.

Auf dem Segment

In der ersten Abbildung nimmt die Funktion den größten (max y) und den kleinsten (min y) Wert an stationären Punkten innerhalb des Segments [-6;6] an.

Betrachten Sie den in der zweiten Abbildung dargestellten Fall. Ändern wir das Segment in . In diesem Beispiel wird der kleinste Wert der Funktion an einem stationären Punkt erreicht und der größte an dem Punkt, dessen Abszisse der rechten Grenze des Intervalls entspricht.

In Abbildung 3 sind die Randpunkte des Segments [-3;2] die Abszissen der Punkte, die dem größten und kleinsten Wert der Funktion entsprechen.

In einem offenen Intervall

In der vierten Abbildung nimmt die Funktion die größten (max y) und kleinsten (min y) Werte an stationären Punkten an, die sich innerhalb des offenen Intervalls (-6;6) befinden.

Über das Intervall können keine Rückschlüsse auf den größten Wert gezogen werden.

Im Unendlichen

In dem in der siebten Abbildung dargestellten Beispiel nimmt die Funktion den größten Wert (max y) an einem stationären Punkt mit der Abszisse x=1 an und der kleinste Wert (min y) wird am rechten Rand des Intervalls erreicht. Bei minus Unendlich nähern sich die Funktionswerte asymptotisch y=3 an.

Im Intervall erreicht die Funktion weder den kleinsten noch den größten Wert. Wenn sich x=2 von rechts nähert, tendieren die Funktionswerte zu minus Unendlich (die Linie x=2 ist eine vertikale Asymptote), und wenn die Abszisse zu plus Unendlich tendiert, nähern sich die Funktionswerte asymptotisch y=3 an. Eine grafische Darstellung dieses Beispiels ist in Abbildung 8 dargestellt.

Algorithmus zum Finden der größten und kleinsten Werte einer stetigen Funktion auf einem Segment.

Schreiben wir einen Algorithmus, der es uns ermöglicht, den größten und kleinsten Wert einer Funktion in einem Segment zu finden.

1. Wir finden den Definitionsbereich der Funktion und prüfen, ob er das gesamte Segment enthält.
2. Wir finden alle Punkte, an denen die erste Ableitung nicht existiert und die im Segment enthalten sind (normalerweise findet man solche Punkte in Funktionen mit einem Argument unter dem Modulzeichen und in Potenzfunktionen mit einem gebrochen-rationalen Exponenten). Wenn es keine solchen Punkte gibt, fahren Sie mit dem nächsten Punkt fort.
3. Wir ermitteln alle stationären Punkte, die in das Segment fallen. Dazu setzen wir es mit Null gleich, lösen die resultierende Gleichung und wählen geeignete Wurzeln aus. Wenn es keine stationären Punkte gibt oder keiner davon in das Segment fällt, fahren Sie mit dem nächsten Punkt fort.
4. Wir berechnen die Werte der Funktion an ausgewählten stationären Punkten (falls vorhanden), an Punkten, an denen die erste Ableitung nicht existiert (falls vorhanden) sowie bei x=a und x=b.
5. Aus den erhaltenen Werten der Funktion wählen wir den größten und kleinsten aus – es handelt sich um den erforderlichen größten bzw. kleinsten Wert der Funktion.

Lassen Sie uns den Algorithmus zum Lösen eines Beispiels analysieren, um den größten und kleinsten Wert einer Funktion auf einem Segment zu finden.

Beispiel.

Finden Sie den größten und kleinsten Wert einer Funktion

• auf dem Segment;
• auf dem Segment [-4;-1] .

Lösung.

Der Definitionsbereich einer Funktion ist die gesamte Menge der reellen Zahlen, mit Ausnahme von Null. Beide Segmente fallen in den Definitionsbereich.

Finden Sie die Ableitung der Funktion nach:

Offensichtlich existiert die Ableitung der Funktion an allen Punkten der Segmente und [-4;-1].

Wir ermitteln stationäre Punkte aus der Gleichung. Die einzige echte Wurzel ist x=2. Dieser stationäre Punkt fällt in das erste Segment.

Für den ersten Fall berechnen wir die Werte der Funktion an den Enden des Segments und am stationären Punkt, also für x=1, x=2 und x=4:

Daher der größte Wert der Funktion wird bei x=1 und dem kleinsten Wert erreicht – bei x=2.

Für den zweiten Fall berechnen wir die Funktionswerte nur an den Enden des Segments [-4;-1] (da es keinen einzigen stationären Punkt enthält):

Lösung.

Beginnen wir mit dem Definitionsbereich der Funktion. Das quadratische Trinom im Nenner des Bruchs darf nicht verschwinden:

Es lässt sich leicht überprüfen, ob alle Intervalle aus der Problemstellung zum Definitionsbereich der Funktion gehören.

Lassen Sie uns die Funktion differenzieren:

Offensichtlich existiert die Ableitung im gesamten Definitionsbereich der Funktion.

Lassen Sie uns stationäre Punkte finden. Die Ableitung geht bei Null gegen Null. Dieser stationäre Punkt liegt in den Intervallen (-3;1] und (-3;2).

Jetzt können Sie die an jedem Punkt erhaltenen Ergebnisse mit dem Diagramm der Funktion vergleichen. Blaue gepunktete Linien zeigen Asymptoten an.

An diesem Punkt können wir mit der Ermittlung des größten und kleinsten Wertes der Funktion abschließen. Die in diesem Artikel besprochenen Algorithmen ermöglichen es Ihnen, mit einem Minimum an Aktionen Ergebnisse zu erzielen. Es kann jedoch sinnvoll sein, zunächst die Anstiegs- und Abfallintervalle der Funktion zu bestimmen und erst danach Rückschlüsse auf den größten und kleinsten Wert der Funktion in einem beliebigen Intervall zu ziehen. Dies ergibt ein klareres Bild und eine schlüssige Begründung der Ergebnisse.

Definition3 . 3 Sei eine Funktion, ihr Definitionsbereich und ein (offenes) Intervall (vielleicht mit und/oder) 7 . Rufen wir die Funktion auf kontinuierlich im Intervall, wenn es an jedem Punkt stetig ist, das heißt, für jeden, den es gibt (in Kurzform:

Sei nun ein (geschlossenes) Segment in . Rufen wir die Funktion auf kontinuierlich auf dem Segment, wenn im Intervall stetig, also rechts am Punkt stetig und links am Punkt stetig

Beispiel3 . 13 Betrachten Sie die Funktion (Heaviside-Funktion) auf dem Segment , . Dann ist es auf dem Segment stetig (obwohl es an der Stelle eine Diskontinuität erster Art aufweist).

Abb. 3.15. Diagramm der Heaviside-Funktion

Eine ähnliche Definition kann für Halbintervalle der Form und gegeben werden, einschließlich der Fälle und. Wir können diese Definition jedoch wie folgt auf den Fall einer beliebigen Teilmenge verallgemeinern. Lassen Sie uns zunächst das Konzept vorstellen induziert zu Basen: Sei eine Basis, deren Endungen alle nichtleere Schnittpunkte mit haben. Bezeichnen wir mit und betrachten wir die Menge aller. Es ist dann leicht zu überprüfen, ob das Set vorhanden ist wird die Basis sein. Somit gelten für die Basen , und , wobei , und die Basen unpunktierter zweiseitiger (linker bzw. rechter) Umgebungen eines Punktes sind (siehe deren Definition am Anfang des aktuellen Kapitels).

Definition3 . 4 Rufen wir die Funktion auf kontinuierlich am Set, Wenn

Es ist leicht zu erkennen, dass diese Definition dann mit den oben speziell für das Intervall und Segment angegebenen übereinstimmt.

Denken Sie daran, dass alle Elementarfunktionen an allen Punkten ihres Definitionsbereichs stetig sind und daher auch in allen Intervallen und Segmenten, die in ihrem Definitionsbereich liegen, stetig sind.

Da die Kontinuität auf einem Intervall und Segment punktweise definiert ist, gilt der Satz, der eine unmittelbare Konsequenz aus Satz 3.1 ist:

Satz3 . 5 Lassen Und -- Funktionen und -- Intervall oder Segment, das darin liegt . Lassen Und kontinuierlich für . Dann die Funktionen , , kontinuierlich für . Wenn zusätzlich Vor allen , dann die Funktion ist auch kontinuierlich eingeschaltet .

Aus diesem Satz folgt, ebenso wie aus Satz 3.1 – Satz 3.3, folgende Aussage:

Angebot3 . 4 Ein Haufen Alle Funktionen sind in einem Intervall oder Segment kontinuierlich -- das ist ein linearer Raum:

Eine komplexere Eigenschaft einer stetigen Funktion wird durch den folgenden Satz ausgedrückt.

Satz3 . 6 (über die Wurzel einer stetigen Funktion) Lassen Sie die Funktion kontinuierlich auf dem Segment , Und Und -- Anzahl verschiedener Zeichen. (Aus Gründen der Bestimmtheit gehen wir davon aus , A .) Dann gibt es mindestens einen solchen Wert , Was (das heißt, es gibt mindestens eine Wurzel Gleichungen ).

Nachweisen. Schauen wir uns die Mitte des Segments an. Dann heißt es entweder, oder, oder. Im ersten Fall wird die Wurzel gefunden: Das ist . Betrachten Sie in den verbleibenden beiden Fällen den Teil des Segments, an dessen Enden die Funktion Werte mit unterschiedlichen Vorzeichen annimmt: im Fall oder im Fall . Wir bezeichnen die ausgewählte Hälfte des Segments mit und wenden das gleiche Verfahren darauf an: Teilen Sie es in zwei Hälften und , wo , und finden Sie . Falls die Wurzel gefunden wird; In diesem Fall betrachten wir das Segment weiter , falls - Segment usw.

Abb. 3.16. Aufeinanderfolgende Teilungen eines Segments in zwei Hälften

Wir erhalten, dass entweder irgendwann die Wurzel gefunden wird oder ein System verschachtelter Segmente konstruiert wird

wobei jedes nachfolgende Segment halb so lang ist wie das vorherige. Die Folge ist nicht abnehmend und nach oben begrenzt (z. B. durch die Zahl); daher (nach Satz 2.13) hat es einen Grenzwert. Folge - nicht steigend und nach unten begrenzt (z. B. durch die Zahl); das bedeutet, dass es eine Grenze gibt. Da die Längen der Segmente einen abnehmenden geometrischen Verlauf (mit Nenner) bilden, tendieren sie gegen 0, und , also . Sagen wir es jetzt. Dann

Und

da die Funktion stetig ist. Allerdings ergibt sich durch die Konstruktion der Folgen und , und , dass nach dem Satz über den Grenzübergang in der Ungleichung (Satz 2.7) und , das heißt, und . Dies bedeutet, dass und die Wurzel der Gleichung ist.

Beispiel3 . 14 Betrachten Sie die Funktion auf dem Segment. Da und Zahlen mit unterschiedlichen Vorzeichen sind, geht die Funktion irgendwann im Intervall auf 0 über. Das bedeutet, dass die Gleichung eine Wurzel hat.

Abb. 3.17. Grafische Darstellung der Wurzel der Gleichung

Der bewährte Satz gibt uns tatsächlich eine Möglichkeit, die Wurzel zumindest näherungsweise mit einem im Voraus festgelegten Genauigkeitsgrad zu finden. Dies ist die Methode, ein Segment in zwei Hälften zu teilen, die im Beweis des Theorems beschrieben wird. Wir werden diese und andere, effektivere Methoden zur näherungsweisen Wurzelfindung im Folgenden genauer kennenlernen, nachdem wir das Konzept und die Eigenschaften einer Ableitung untersucht haben.

Beachten Sie, dass der Satz nicht besagt, dass die Wurzel eindeutig ist, wenn ihre Bedingungen erfüllt sind. Wie die folgende Abbildung zeigt, kann es mehr als eine Wurzel geben (in der Abbildung sind es 3).

Abb. 3.18: Mehrere Wurzeln einer Funktion, die an den Enden des Segments Werte mit unterschiedlichen Vorzeichen annimmt

Wenn jedoch eine Funktion auf einem Segment, an dessen Enden sie Werte unterschiedlicher Vorzeichen annimmt, monoton zunimmt oder monoton abnimmt, dann ist die Wurzel eindeutig, da eine streng monotone Funktion jeden ihrer Werte an genau einem Punkt annimmt , einschließlich des Wertes 0.

Abb. 3.19: Eine monotone Funktion kann nicht mehr als eine Wurzel haben

Eine unmittelbare Konsequenz des Satzes über die Wurzel einer stetigen Funktion ist der folgende Satz, der für sich genommen in der mathematischen Analyse sehr wichtig ist.

Satz3 . 7 (über den Zwischenwert einer stetigen Funktion) Lassen Sie die Funktion kontinuierlich auf dem Segment Und (Der Bestimmtheit halber gehen wir davon aus ). Lassen -- eine Zahl, die dazwischen liegt Und . Dann gibt es so einen Punkt , Was .

Abb. 3.20: Die kontinuierliche Funktion nimmt jeden Zwischenwert an

Nachweisen. Betrachten Sie die Hilfsfunktion , Wo . Dann Und . Die Funktion ist offensichtlich stetig, und nach dem vorherigen Satz gibt es einen Punkt mit . Aber diese Gleichheit bedeutet das.

Beachten Sie, dass die Funktion möglicherweise nicht alle Zwischenwerte annimmt, wenn sie nicht stetig ist. Beispielsweise nimmt die Heaviside-Funktion (siehe Beispiel 3.13) die Werte an, nimmt aber nirgends, auch nicht im Intervall, beispielsweise einen Zwischenwert an. Tatsache ist, dass die Heaviside-Funktion an einem Punkt, der genau im Intervall liegt, eine Diskontinuität aufweist.

Um die Eigenschaften von auf einem Intervall stetigen Funktionen weiter zu untersuchen, benötigen wir die folgende subtile Eigenschaft des Systems der reellen Zahlen (wir haben sie bereits in Kapitel 2 im Zusammenhang mit dem Satz über den Grenzwert einer monoton wachsenden beschränkten Funktion erwähnt): z jede nach unten beschränkte Menge (d. h. so, dass für alle und einige; die Zahl heißt Unterkante Sets) verfügbar exakte Unterkante, also die größte der Zahlen, die für alle gelten. Wenn eine Menge nach oben beschränkt ist, gilt dies auch genaue Obergrenze: Dies ist das kleinste von Oberseiten(wofür für alle).

Abb. 3.21: Untere und obere Grenze einer beschränkten Menge

Wenn, dann gibt es eine nicht zunehmende Folge von Punkten, die dazu tendiert. Auf die gleiche Weise gilt: Wenn , dann gibt es eine nicht abnehmende Folge von Punkten, die dazu tendiert.

Wenn ein Punkt zur Menge gehört, dann ist er das kleinste Element dieser Menge: ; ebenso wenn , Das .

Darüber hinaus benötigen wir für weitere Informationen Folgendes

Lemma3 . 1 Lassen -- Kontinuierliche Funktion auf einem Segment , und viele diese Punkte , in welchem (oder , oder ) ist nicht leer. Dann im Überfluss es gibt einen kleinsten Wert , so dass Vor allen .

Abb. 3.22: Das kleinste Argument, bei dem die Funktion den angegebenen Wert annimmt

Nachweisen. Da es sich um eine beschränkte Menge handelt (sie ist Teil eines Segments), hat sie ein Infimum. Dann gibt es eine nichtsteigende Folge , , so dass für . Darüber hinaus durch die Definition einer Menge. Wenn wir also zum Grenzwert übergehen, erhalten wir einerseits

und andererseits aufgrund der Kontinuität der Funktion,

Das heißt, der Punkt gehört zur Menge und.

Für den Fall, dass die Menge durch die Ungleichung definiert ist, haben wir für alle und durch den Satz über den Grenzübergang in der Ungleichung erhalten wir

von wo , was bedeutet, dass und . Ähnlich verhält es sich im Fall der Ungleichung, wenn man bis zur Grenze der Ungleichung geht

von wo, und.

Satz3 . 8 (über die Beschränktheit einer stetigen Funktion) Lassen Sie die Funktion kontinuierlich auf dem Segment . Dann begrenzt auf , das heißt, es gibt eine solche Konstante , Was Vor allen .

Abb. 3.23: Eine auf einem Segment stetige Funktion ist beschränkt

Nachweisen. Nehmen wir das Gegenteil an: Lassen Sie es nicht beispielsweise von oben einschränken. Dann sind nicht alle Mengen , , , leer. Nach dem vorherigen Lemma hat jede dieser Mengen den kleinsten Wert , . Zeigen wir das

Wirklich, . Wenn beispielsweise ein Punkt von zwischen und liegt, dann

das heißt, ein Zwischenwert zwischen und . Das bedeutet, dass es nach dem Satz über den Zwischenwert einer stetigen Funktion einen Punkt gibt, so dass , Und . Aber entgegen der Annahme, dass es sich um den kleinsten Wert der Menge handelt. Daraus folgt für alle.

Auf die gleiche Weise wird weiter bewiesen, dass für alle, für alle usw. eine steigende Folge oben durch die Zahl begrenzt ist. Deshalb existiert es. Aus der Stetigkeit der Funktion folgt, dass es sie gibt , Aber bei , es gibt also keine Begrenzung. Der resultierende Widerspruch beweist, dass die Funktion nach oben beschränkt ist.

Auf ähnliche Weise wird bewiesen, dass es nach unten beschränkt ist, was die Aussage des Satzes impliziert.

Offensichtlich ist es unmöglich, die Bedingungen des Satzes abzuschwächen: Wenn eine Funktion nicht stetig ist, muss sie nicht auf ein Intervall beschränkt sein (wir geben als Beispiel die Funktion).

auf dem Segment. Diese Funktion ist nicht auf das Intervall beschränkt, da at einen Unstetigkeitspunkt zweiter Art hat, so dass bei . Es ist auch unmöglich, ein Segment in der Bedingung des Satzes durch ein Intervall oder Halbintervall zu ersetzen: Betrachten Sie als Beispiel dieselbe Funktion in einem Halbintervall. Die Funktion ist in diesem Halbintervall stetig, aber unbeschränkt, da bei .

Das Finden der besten Konstanten, die zur Begrenzung einer Funktion von oben und unten in einem bestimmten Intervall verwendet werden können, führt uns natürlich zu dem Problem, das Minimum und das Maximum einer stetigen Funktion in diesem Intervall zu finden. Die Möglichkeit, dieses Problem zu lösen, wird durch den folgenden Satz beschrieben.

Satz3 . 9 (über das Erreichen eines Extremums durch eine stetige Funktion) Lassen Sie die Funktion kontinuierlich auf dem Segment . Dann gibt es einen Punkt , so dass Vor allen (also -- Mindestpunktzahl: ), und da ist ein Punkt , so dass Vor allen (also -- Höchstpunktzahl: ). Mit anderen Worten, das Minimum und das Maximum 8 Werte einer stetigen Funktion auf einem Segment existieren und werden an einigen Punkten erreicht Und dieses Segment.

Abb. 3.24: Eine auf einem Segment stetige Funktion erreicht ein Maximum und ein Minimum

Nachweisen. Da die Funktion nach dem vorherigen Satz durch oben begrenzt ist, gibt es eine genaue Obergrenze für die Werte der Funktion durch – Zahl . Somit sind die Mengen , ,..., ,... nicht leer und enthalten nach dem vorherigen Lemma die kleinsten Werte: , . Diese nehmen nicht ab (diese Aussage wird genauso bewiesen wie im vorherigen Satz):

und werden von oben begrenzt durch . Daher gibt es nach dem Satz über den Grenzwert einer monoton beschränkten Folge einen Grenzwert Da , Dann

durch den Satz über den Grenzübergang in der Ungleichung, d. h. . Aber mit allen, auch. Daraus ergibt sich, dass das Maximum der Funktion im Punkt erreicht wird.

Die Existenz eines Minimalpunktes wird auf ähnliche Weise bewiesen.

In diesem Satz, wie auch im vorherigen, ist es unmöglich, die Bedingungen abzuschwächen: Wenn die Funktion nicht stetig ist, kann es sein, dass sie ihren Maximal- oder Minimalwert auf dem Segment nicht erreicht, selbst wenn sie begrenzt ist. Nehmen wir zum Beispiel die Funktion

auf dem Segment. Diese Funktion ist (offensichtlich) auf das Intervall und beschränkt , nimmt jedoch an keinem Punkt des Segments den Wert 1 an (beachten Sie, dass , nicht 1). Tatsache ist, dass diese Funktion am Punkt eine Diskontinuität erster Art aufweist, so dass sie am Grenzwert nicht gleich dem Wert der Funktion am Punkt 0 ist. Darüber hinaus ist eine kontinuierliche Funktion, die auf einem Intervall oder einer anderen Menge definiert ist, nicht gleich ein geschlossenes Segment (auf einem halben Intervall, einer halben Achse) kann auch keine Extremwerte annehmen. Betrachten Sie als Beispiel eine Funktion im Intervall. Es ist offensichtlich, dass die Funktion stetig ist und dass und die Funktion an keinem Punkt des Intervalls den Wert 0 oder den Wert 1 annimmt. Betrachten wir auch die Funktion auf der Achswelle. Diese Funktion ist stetig auf , nimmt zu, nimmt am Punkt ihren Minimalwert 0 an, nimmt aber an keinem Punkt einen Maximalwert an (obwohl sie von oben durch die Zahl und begrenzt ist

Definition. Wenn die Funktion F(X) ist auf dem Intervall [ definiert a, b], ist an jedem Punkt des Intervalls stetig ( a, b), am Punkt A rechts durchgehend, am Punkt B ist auf der linken Seite stetig, dann sagen wir, dass die Funktion F(X) kontinuierlich auf dem Segment [a, b].

Mit anderen Worten, die Funktion F(X) ist stetig im Intervall [ a, b], wenn drei Bedingungen erfüllt sind:

1) "X 0 Î( a, b): F(X) = F(X 0);

2) F(X) = F(A);

3) F(X) = F(B).

Für auf einem Intervall stetige Funktionen betrachten wir einige Eigenschaften, die wir in Form der folgenden Sätze formulieren, ohne Beweise durchzuführen.

Satz 1. Wenn die Funktion F(X) ist stetig im Intervall [ a, b], dann erreicht es in diesem Segment seine Minimal- und Maximalwerte.

Dieser Satz besagt (Abb. 1.15), dass auf dem Segment [ a, b] Es gibt so einen Punkt X 1 das F(X 1) £ F(X) für jeden X aus [ a, b] und dass es einen Sinn hat X 2 (X 2 О[ a, b]) so dass " XÎ[ a, b] (F(X 2)³ F(X)).

Bedeutung F(X 1) ist der größte für eine gegebene Funktion auf [ a, b], A F(X 2) – der Kleinste. Bezeichnen wir: F(X 1) = M, F(X 2) =M. Da für F(X) die Ungleichung gilt: „ XÎ[ a, b] M£ F(X) £ M, dann erhalten wir das folgende Korollar aus Satz 1.

Folge. Wenn die Funktion F(X) auf einem Intervall stetig ist, dann ist es auf dieses Intervall beschränkt.

Satz 2. Wenn die Funktion F(X) ist stetig im Intervall [ a,b] und an den Enden des Segments Werte mit unterschiedlichen Vorzeichen annimmt, dann gibt es einen solchen internen Punkt X 0 Segment [ a, b], bei dem die Funktion auf 0 geht, d. h. $ X 0 Î ( a, b) (F(X 0) = 0).

Dieser Satz besagt, dass der Graph einer Funktion y = f(X), kontinuierlich im Intervall [ a, b], schneidet die Achse Ochse mindestens einmal, wenn die Werte F(A) Und F(B) haben entgegengesetzte Vorzeichen. Also (Abb. 1.16) F(A) > 0, F(B) < 0 и функция F(X) wird punktuell 0 X 1 , X 2 , X 3 .

Satz 3. Lassen Sie die Funktion F(X) ist stetig im Intervall [ a, b], F(A) = A, F(B) = B Und A¹ B. (Abb. 1.17). Dann für eine beliebige Zahl C, eingeschlossen zwischen den Zahlen A Und B, es gibt einen solchen inneren Punkt X 0 Segment [ a, b], Was F(X 0) = C.

Folge. Wenn die Funktion F(X) ist stetig im Intervall [ a, b], M– kleinster Wert F(X), M– der größte Wert der Funktion F(X) auf dem Segment [ a, b], dann nimmt die Funktion (mindestens einmal) einen beliebigen Wert an M, abgeschlossen zwischen M Und M, und daher das Segment [ m, M] ist die Menge aller Funktionswerte F(X) auf dem Segment [ a, b].

Beachten Sie, dass, wenn eine Funktion im Intervall stetig ist ( a, b) oder hat auf dem Segment [ a, b] Diskontinuitätspunkte, dann sind die Sätze 1, 2, 3 für eine solche Funktion nicht mehr wahr.

Betrachten Sie abschließend den Satz über die Existenz einer Umkehrfunktion.

Satz 4. Lassen F(X) ist im Intervall stetig X, erhöht (oder verringert) um X und hat einen Wertebereich Y. Dann für die Funktion y = f(X) gibt es eine Umkehrfunktion X= J(j), definiert auf dem Intervall Y, kontinuierlich und zunehmend (oder abnehmend) um Y mit mehreren Bedeutungen X.

Kommentar. Lassen Sie die Funktion X= J(j) ist die Umkehrung der Funktion F(X). Da das Argument normalerweise mit bezeichnet wird X, und die Funktion durch j, dann schreiben wir die Umkehrfunktion in die Form y =J(X).

Beispiel 1. Funktion y = x 2 (Abb. 1.8, a) am Set X= }