FUNKCIJŲ SAVYBĖS, NUOLATINIŲ INTERVIU

Panagrinėkime kai kurias funkcijų, nuolatinių intervale, savybes. Šias savybes pateikiame be įrodymų.

Funkcija y = f(x) paskambino ištisinis segmente [a, b], jei jis yra ištisinis visuose vidiniuose šios atkarpos taškuose, o jos galuose, t.y. taškuose a Ir b, yra ištisinis atitinkamai dešinėje ir kairėje.

1 teorema. Funkcija, kuri tęsiasi intervale [ a, b], bent viename šios atkarpos taške reikšmė yra didžiausia, o bent viename taške – mažiausia.

Teorema teigia, kad jei funkcija y = f(x) yra nuolatinis intervale [ a, b], tada yra bent vienas taškas x 1 Î [ a, b] toks, kad funkcijos reikšmė f(x)šiuo metu bus didžiausia iš visų jo verčių šiame segmente: f(x 1) ≥ f(x). Panašiai yra toks punktas x 2, kurioje funkcijos reikšmė bus mažiausia iš visų segmento reikšmių: f(x 1) ≤ f(x).

Akivaizdu, kad tokių taškų gali būti keli, pavyzdžiui, paveikslėlyje parodyta, kad funkcija f(x) dviejuose taškuose įgauna mažiausią reikšmę x 2 Ir x 2 ".

komentuoti. Teoremos teiginys gali tapti neteisingas, jei atsižvelgsime į funkcijos reikšmę intervale ( a, b). Iš tiesų, jei atsižvelgsime į funkciją y = x(0, 2), tada jis yra tęstinis šiame intervale, bet nepasiekia nei didžiausių, nei mažiausių verčių: jis pasiekia šias reikšmes intervalo galuose, bet galai nepriklauso į mūsų domeną.

Be to, teorema nustoja galioti nenutrūkstančioms funkcijoms. Pateikite pavyzdį.

Pasekmė. Jei funkcija f(x) yra nuolatinis [ a, b], šiame segmente jis yra ribotas.

2 teorema. Tegul funkcija y = f(x) yra nuolatinis intervale [ a, b] ir šio segmento galuose paima skirtingų ženklų reikšmes, tada atkarpos viduje yra bent vienas taškas x = C, kurioje funkcija pereina į nulį: f(C)= 0, kur a< C< b

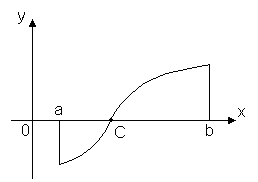
Ši teorema turi paprastą geometrinę reikšmę: jeigu tolydžios funkcijos grafiko taškai y = f(x), atitinkantis segmento galus [ a, b] guli priešingose ​​ašies pusėse Jautis, tada šis grafikas kerta ašį bent viename atkarpos taške Jautis. Nenutrūkstamos funkcijos gali neturėti šios savybės.

Ši teorema leidžia apibendrinti.

3 teorema (tarpinės reikšmės teorema). Tegul funkcija y = f(x) yra nuolatinis intervale [ a, b] Ir f(a) = A, f(b) = B. Tada už bet kokį skaičių C, sudaryta tarp A Ir B, šiame segmente yra toks taškas CÎ [ a, b], Ką f(c) = C.

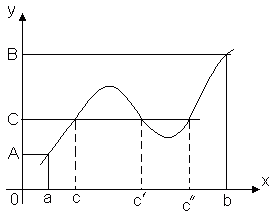
Ši teorema geometriškai akivaizdi. Apsvarstykite funkcijos grafiką y = f(x). Leisti f(a) = A, f(b) = B. Tada bet kokia tiesi linija y = C, Kur C– bet koks skaičius tarp A Ir B, kirs funkcijos grafiką bent viename taške. Susikirtimo taško abscisė bus ta vertė x = C, kuriame f(c) = C.

Taigi nuolatinė funkcija, pereinanti nuo vienos reikšmės prie kitos, būtinai pereina visas tarpines reikšmes. Visų pirma:

Pasekmė. Jei funkcija y = f(x) yra nenutrūkstamas per tam tikrą intervalą ir įgauna didžiausią ir mažiausią reikšmes, tada šiame intervale bent kartą paima bet kokią reikšmę, esančią tarp mažiausios ir didžiausios reikšmių.

IŠVEDINĖ VEIKLA IR JO TAIKYMAS. IŠVESTINĖS MEDŽIAGOS APIBRĖŽIMAS

Leiskite mums atlikti tam tikrą funkciją y=f(x), apibrėžtas tam tikru intervalu. Kiekvienai argumento vertei x iš šio intervalo funkcija y=f(x) turi tam tikrą prasmę.

Apsvarstykite dvi argumentų reikšmes: pradinę x 0 ir naujas x.

Skirtumas x–x 0 vadinamas padidinus argumentą x taške x 0 ir žymimas Δx. Taigi, Δx = x – x 0 (argumento padidėjimas gali būti teigiamas arba neigiamas). Iš šios lygybės išplaukia, kad x=x 0 +Δx, t.y. pradinė kintamojo reikšmė šiek tiek padidėjo. Tada, jei taške x 0 funkcijos reikšmė buvo f(x 0 ), tada naujame taške x funkcija ims reikšmę f(x) = f(x 0 +Δx).

Skirtumas y-y 0 = f(x) – f(x 0 ) paskambino funkcijos padidėjimas y = f(x) taške x 0 ir yra pažymėtas simboliu Δy. Taigi,

Paprastai pradinė argumento reikšmė x 0 laikoma fiksuota, o nauja vertė x– kintamasis. Tada y 0 = f(x 0 ) pasirodo esanti pastovi, ir y = f(x)– kintamasis. Prieaugiai Δy Ir Δx taip pat bus kintamieji ir (1) formulė tai rodo Dy yra kintamojo funkcija Δx.

Sukurkime funkcijos prieaugio ir argumento prieaugio santykį

Raskime šio santykio ribą ties Δx→0. Jei ši riba egzistuoja, tada ji vadinama šios funkcijos išvestine f(x) taške x 0 ir pažymėkite f "(x 0). Taigi,

Darinysšią funkciją y = f(x) taške x 0 vadinama funkcijos prieaugio santykio Δ riba y prie argumento prieaugio Δ x, kai pastarasis savavališkai linkęs į nulį.

Atkreipkite dėmesį, kad tos pačios funkcijos išvestinė skirtinguose taškuose x gali įgauti skirtingas vertybes, t.y. išvestinę galima laikyti argumento funkcija x. Ši funkcija yra paskirta f "(x)

Išvestinė žymima simboliais f "(x),y“, . Konkreti išvestinės vertės vertė x = ažymimas f "(a) arba y "| x=a.

Funkcijos išvestinės radimo operacija f(x) vadinamas šios funkcijos diferencijavimu.

Norėdami tiesiogiai rasti išvestį pagal apibrėžimą, galite naudoti šiuos veiksmus: nykščio taisyklė:

Pavyzdžiai.

MECHANINIS IŠVEDINIMO JAUSMAS

Iš fizikos žinoma, kad tolygaus judėjimo dėsnis turi formą s = v t, Kur s– kelias nukeliavo į laiko akimirką t, v– tolygaus judėjimo greitis.

Tačiau, nes Dauguma gamtoje vykstančių judesių yra netolygi, tada apskritai greitis, taigi ir atstumas s priklausys nuo laiko t, t.y. bus laiko funkcija.

Taigi, tegul materialus taškas juda tiesia linija viena kryptimi pagal dėsnį s=s(t).

Pažymėkime tam tikrą laiko momentą t 0 . Šiuo metu taškas praėjo kelią s=s(t 0 ). Nustatykime greitį v materialus taškas laiko momentu t 0 .

Norėdami tai padaryti, apsvarstykite kitą laiko momentą t 0 + Δ t. Tai atitinka nueitą kelią s =s(t 0 + Δ t). Tada per tam tikrą laiką Δ t taškas nukeliavo keliu Δs =s(t 0 + Δ t)–s(t).

Apsvarstykime požiūrį. Jis vadinamas vidutiniu greičiu laiko intervale Δ t. Vidutinis greitis negali tiksliai apibūdinti taško judėjimo greičio šiuo metu t 0 (nes judėjimas netolygus). Norint tiksliau išreikšti šį tikrąjį greitį naudojant vidutinį greitį, reikia skirti trumpesnį laiko tarpą Δ t.

Taigi, judėjimo greitis tam tikru laiko momentu t 0 (momentinis greitis) yra vidutinio greičio riba intervale nuo t 0 iki t 0 +Δ t, kai Δ t→0:

,

tie. netolygus greitis tai yra nuvažiuoto atstumo laiko atžvilgiu išvestinė.

GEOMETRINĖ IŠVEDINĖS REIKŠMĖ

Pirmiausia pristatykime kreivės liestinės apibrėžimą tam tikrame taške.

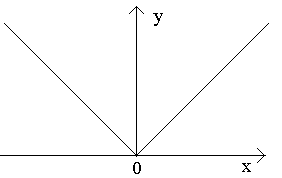
Turėkime kreivę ir fiksuotą tašką M 0(žr. pav.) Apsvarstykite kitą dalyką Mšią kreivę ir nubrėžkite sekantą M 0 M. Jei taškas M pradeda judėti išilgai kreivės, o taškas M 0 lieka nejudantis, tada sekantas pakeičia savo padėtį. Jei su neribotu taško aproksimavimu M išilgai kreivės iki taško M 0 bet kurioje pusėje sekantas yra linkęs užimti tam tikros tiesės padėtį M 0 T, tada tiesiai M 0 T vadinama kreivės liestine tam tikrame taške M 0.

Tai., liestinėį kreivę tam tikrame taške M 0 vadinama sekanto ribine padėtimi M 0 M kai taškas M išilgai kreivės linksta į tašką M 0.

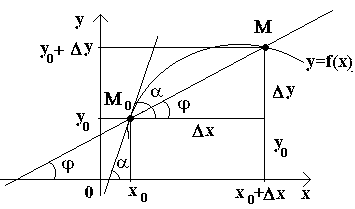
Dabar panagrinėkime nuolatinę funkciją y=f(x) ir šią funkciją atitinkančią kreivę. Tam tikra verte X 0 funkcija įgauna reikšmę y 0 =f(x 0).Šios vertybės x 0 ir y 0 kreivėje atitinka tašką M 0 (x 0 ; y 0). Pateikime argumentą x 0 prieaugis Δ X. Nauja argumento reikšmė atitinka padidintą funkcijos reikšmę y 0 +Δ y=f(x 0 –Δ x). Mes suprantame esmę M(x 0+Δ x; y 0+Δ y). Nubrėžkime sekantą M 0 M ir φ pažymime kampą, kurį sudaro atkarpa su teigiama ašies kryptimi Jautis. Sukurkime ryšį ir pastebėkime tai.

Jei dabar Δ x→0, tada dėl funkcijos Δ tęstinumo adresu→0, taigi ir taškas M, judėdamas išilgai kreivės, be apribojimų artėja prie taško M 0. Tada sekantas M 0 M taške bus linkęs užimti kreivės liestinės padėtį M 0, o kampas φ→α ties Δ x→0, kur α žymi kampą tarp liestinės ir teigiamos ašies krypties Jautis. Kadangi funkcija tan φ nuolat priklauso nuo φ, kai φ≠π/2, tada φ→α tan φ → tan α ir dėl to liestinės nuolydis bus:

tie. f "(x)= tg α .

Taigi, geometriškai y "(x 0) reiškia šios funkcijos grafiko liestinės nuolydį taške x 0, t.y. už nurodytą argumento reikšmę x, išvestinė lygi kampo, kurį sudaro funkcijos grafiko liestinė, tangentei f(x) atitinkamame taške M 0 (x; y) su teigiama ašies kryptimi Jautis.

Pavyzdys. Raskite kreivės liestinės nuolydį y = x 2 taške M(-1; 1).

Mes jau matėme anksčiau, kad ( x 2)" = 2X. Bet kreivės liestinės kampinis koeficientas yra tan α = y"| x=-1 = – 2.

FUNKCIJŲ DIFERENCIJUMAS. DIFERENCIJOS FUNKCIJOS TĘSTYMAS

Funkcija y=f(x) paskambino skiriasi tam tikru momentu x 0, jei jis turi tam tikrą išvestinę šiame taške, t.y. jei santykio riba egzistuoja ir yra baigtinė.

Jei funkcija yra diferencijuojama kiekviename tam tikros atkarpos taške [ A; b] arba intervalas ( A; b), tada jie sako, kad ji skiriasi segmente [ A; b] arba atitinkamai intervale ( A; b).

Galioja tokia teorema, nustatanti ryšį tarp diferencijuojamųjų ir tolydžių funkcijų.

Teorema. Jei funkcija y=f(x) tam tikru momentu skiriasi x 0, tada šiuo metu jis yra tęstinis.

Taigi iš funkcijos diferencijavimo išplaukia jos tęstinumas.

Įrodymas. Jeigu , Tai

,

kur α yra be galo mažas dydis, t.y. dydis, linkęs į nulį kaip Δ x→0. Bet tada

Δ y=f "(x 0) Δ x+αΔ x=> Δ y→0 ties Δ x→0, t.y. f(x) – f(x 0)→0 at x→x 0 , o tai reiškia, kad funkcija f(x) ištisinis taške x 0 . Q.E.D.

Taigi funkcija negali turėti išvestinės nutrūkimo taškuose. Priešingai: yra tęstinių funkcijų, kurios kai kuriuose taškuose nėra diferencijuojamos (ty šiuose taškuose neturi išvestinės).

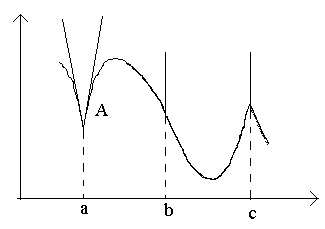
Apsvarstykite paveikslėlyje esančius taškus a, b, c.

Taške a ties Δ x→0 santykis neturi ribos (nes Δ vienpusės ribos skiriasi x→0–0 ir Δ x→0+0). Taške A Grafike nėra apibrėžtos liestinės, tačiau yra dvi skirtingos vienpusės liestinės su nuolydžiais Į 1 ir Į 2. Šio tipo taškai vadinamas kampiniu tašku.

Taške b ties Δ x→0 santykis yra pastovus ženklas, be galo didelis dydis. Funkcija turi begalinę išvestinę. Šiuo metu grafikas turi vertikalią liestinę. Taško tipas – vertikaliosios liestinės „linkos taškas“.

Taške c vienpusiai dariniai – tai be galo dideli skirtingų ženklų kiekiai. Šiuo metu grafike yra dvi sujungtos vertikalios liestinės. Tipas – „grįžimo taškas“ su vertikalia liestine – specialus kampinio taško atvejis.

Toliau pateiktuose paveikslėliuose parodyta, kur funkcija gali pasiekti mažiausią ir didžiausią reikšmę. Kairiajame paveikslėlyje mažiausia ir didžiausia reikšmės yra fiksuotos funkcijos vietinio minimumo ir maksimumo taškuose. Dešiniajame paveikslėlyje - segmento galuose.

Jei funkcija y = f(x) yra nuolatinis intervale [ a, b] , tada jis pasiekia šį segmentą mažiausiai Ir aukščiausios vertės . Tai, kaip jau minėta, gali įvykti tiek ekstremalūs taškai, arba segmento galuose. Todėl norint rasti mažiausiai Ir didžiausios funkcijos reikšmės , nuolatinis intervale [ a, b], turite apskaičiuoti jo reikšmes kritinius taškus ir segmento galuose, o tada iš jų pasirinkite mažiausią ir didžiausią.

Pavyzdžiui, leiskite nustatyti didžiausią funkcijos reikšmę f(x) segmente [ a, b] . Norėdami tai padaryti, turite rasti visus jo kritinius taškus, esančius [ a, b] .

Kritinis taškas vadinamas tašku, kuriame apibrėžta funkcija, ir ji išvestinė arba lygus nuliui, arba neegzistuoja. Tada turėtumėte apskaičiuoti funkcijos reikšmes kritiniuose taškuose. Ir galiausiai, reikėtų palyginti funkcijos reikšmes kritiniuose taškuose ir segmento galuose ( f(a) Ir f(b)). Didžiausias iš šių skaičių bus didžiausia segmento funkcijos reikšmė [a, b] .

Suradimo problemos mažiausios funkcijos reikšmės .

Kartu ieškome mažiausios ir didžiausios funkcijos reikšmių

1 pavyzdys. Raskite mažiausią ir didžiausią funkcijos reikšmes segmente [-1, 2] .

Sprendimas. Raskite šios funkcijos išvestinę. Prilyginkime išvestinę nuliui () ir gaukime du kritinius taškus: ir . Norint rasti mažiausią ir didžiausią funkcijos reikšmes tam tikrame segmente, pakanka apskaičiuoti jos reikšmes atkarpos galuose ir taške, nes taškas nepriklauso atkarpai [-1, 2]. Šios funkcijos reikšmės yra: , , . Tai seka mažiausia funkcijos reikšmė(žemiau esančiame grafike pažymėta raudonai), lygus -7, pasiekiamas dešiniajame atkarpos gale - taške ir didžiausias(taip pat raudona grafike), lygi 9, - kritiniame taške.

Jei funkcija tam tikrame intervale yra ištisinė ir šis intervalas nėra atkarpa (bet yra, pavyzdžiui, intervalas; skirtumas tarp intervalo ir atkarpos: intervalo ribiniai taškai neįtraukiami į intervalą, o atkarpos ribiniai taškai įtraukiami į atkarpą), tada tarp funkcijos reikšmių gali nebūti mažiausio ir didžiausio. Taigi, pavyzdžiui, toliau esančiame paveikslėlyje parodyta funkcija yra nuolatinė ]-∞, +∞[ ir neturi didžiausios reikšmės.

Tačiau bet kokiam intervalui (uždarajam, atviram ar begaliniam) yra teisinga tokia nuolatinių funkcijų savybė.

Norėdami atlikti savęs patikrinimą skaičiavimų metu, galite naudoti internetinė išvestinių priemonių skaičiuoklė .

4 pavyzdys. Raskite mažiausią ir didžiausią funkcijos reikšmes segmente [-1, 3] .

Sprendimas. Šios funkcijos išvestinę randame kaip koeficiento išvestinę:

.

Išvestinę prilyginame nuliui, o tai suteikia mums vieną kritinį tašką: . Ji priklauso segmentui [-1, 3] . Norėdami rasti mažiausią ir didžiausią tam tikro segmento funkcijos reikšmes, randame jos reikšmes segmento galuose ir rastame kritiniame taške:

Palyginkime šias vertes. Išvada: lygi -5/13, taške ir didžiausia vertė lygus 1 taške .

Mes ir toliau kartu ieškome mažiausios ir didžiausios funkcijos reikšmių

Yra dėstytojų, kurie, siekdami surasti mažiausią ir didžiausią funkcijos reikšmes, nepateikia studentams sudėtingesnių nei ką tik aptartų pavyzdžių, ty tų, kurių funkcija yra daugianario ar trupmena, kurios skaitiklis ir vardiklis yra daugianariai. Tačiau tokiais pavyzdžiais neapsiribosime, nes tarp mokytojų yra tokių, kurie mėgsta priversti mokinius mąstyti visapusiškai (išvestinių lentelė). Todėl bus naudojamas logaritmas ir trigonometrinė funkcija.

8 pavyzdys. Raskite mažiausią ir didžiausią funkcijos reikšmes segmente .

Sprendimas. Šios funkcijos išvestinę randame kaip produkto darinys :

Išvestinę prilyginame nuliui, kuri suteikia vieną kritinį tašką: . Tai priklauso segmentui. Norėdami rasti mažiausią ir didžiausią tam tikro segmento funkcijos reikšmes, randame jos reikšmes segmento galuose ir rastame kritiniame taške:

Visų veiksmų rezultatas: funkcija pasiekia mažiausią reikšmę, lygus 0, taške ir taške ir didžiausia vertė, lygus e², taške.

Norėdami atlikti savęs patikrinimą skaičiavimų metu, galite naudoti internetinė išvestinių priemonių skaičiuoklė .

9 pavyzdys. Raskite mažiausią ir didžiausią funkcijos reikšmes segmente .

Sprendimas. Raskite šios funkcijos išvestinę:

Išvestinę prilyginame nuliui:

Vienintelis kritinis taškas priklauso segmentui. Norėdami rasti mažiausią ir didžiausią tam tikro segmento funkcijos reikšmes, randame jos reikšmes segmento galuose ir rastame kritiniame taške:

Išvada: funkcija pasiekia mažiausią reikšmę, lygus , taške ir didžiausia vertė, lygus , taške .

Taikomose ekstremaliose problemose, ieškant mažiausių (maksimalių) funkcijos reikšmių, paprastai reikia rasti minimumą (maksimumą). Bet ne patys minimumai ar maksimumai yra labiau praktiški įdomūs, o tos argumento vertės, kuriomis jos pasiekiamos. Sprendžiant taikomąsias problemas, iškyla papildomas sunkumas – funkcijų, apibūdinančių nagrinėjamą reiškinį ar procesą, sudarymas.

10 pavyzdys. 4 talpos bakas, gretasienio formos su kvadratiniu pagrindu ir atviras viršuje, turi būti skarduotas. Kokio dydžio turi būti bakas, kad jai uždengti būtų sunaudojama kuo mažiau medžiagos?

Sprendimas. Leisti x- pagrindo pusė, h- bako aukštis, S- jo paviršiaus plotas be dangos, V- jo tūris. Bako paviršiaus plotas išreiškiamas formule, t.y. yra dviejų kintamųjų funkcija. Išreikšti S kaip vieno kintamojo funkciją, mes naudojame tai, kad , iš kur . Rastos išraiškos pakeitimas hį formulę S:

Panagrinėkime šią funkciją iki jos kraštutinumo. Jis visur apibrėžiamas ir diferencijuojamas ]0, +∞[ ir

.

Išvestinę prilyginame nuliui () ir randame kritinį tašką. Be to, kai išvestinės nėra, bet ši reikšmė nėra įtraukta į apibrėžimo sritį ir todėl negali būti ekstremumo taškas. Taigi, tai yra vienintelis kritinis taškas. Patikrinkime, ar nėra ekstremumo, naudodami antrąjį pakankamo ženklą. Raskime antrąją išvestinę. Kai antroji išvestinė didesnė už nulį (). Tai reiškia, kad funkcijai pasiekus minimumą . Nuo šio minimumas yra vienintelis šios funkcijos ekstremumas, tai yra mažiausia jos reikšmė. Taigi, bako pagrindo šonas turi būti 2 m, o jo aukštis - .

Norėdami atlikti savęs patikrinimą skaičiavimų metu, galite naudoti

Praktiniu požiūriu didžiausias susidomėjimas yra naudoti išvestinę, kad būtų galima rasti didžiausias ir mažiausias funkcijos reikšmes. Su kuo tai susiję? Maksimalus pelnas, kaštų minimizavimas, optimalios įrangos apkrovos nustatymas... Kitaip tariant, daugelyje gyvenimo sričių tenka spręsti kai kurių parametrų optimizavimo problemas. Ir tai yra didžiausios ir mažiausios funkcijos reikšmių radimo užduotys.

Reikėtų pažymėti, kad didžiausios ir mažiausios funkcijos reikšmės paprastai ieškomos tam tikrame intervale X, kuris yra arba visa funkcijos sritis, arba apibrėžimo srities dalis. Pats intervalas X gali būti atkarpa, atviras intervalas , begalinis intervalas.

Šiame straipsnyje kalbėsime apie tai, kaip rasti didžiausią ir mažiausią vieno kintamojo aiškiai apibrėžtos funkcijos reikšmes y=f(x) .

Puslapio naršymas.

Didžiausia ir mažiausia funkcijos reikšmė – apibrėžimai, iliustracijos.

Trumpai pažvelkime į pagrindinius apibrėžimus.

Didžiausia funkcijos reikšmė kad bet kam nelygybė yra tiesa.

Mažiausia funkcijos reikšmė y=f(x) intervale X vadinama tokia reikšme kad bet kam nelygybė yra tiesa.

Šie apibrėžimai yra intuityvūs: didžiausia (mažiausia) funkcijos reikšmė yra didžiausia (mažiausia) priimtina reikšmė nagrinėjamame intervale ties abscisėmis.

Stacionarūs taškai– tai yra argumento reikšmės, kai funkcijos išvestinė tampa lygi nuliu.

Kodėl ieškant didžiausių ir mažiausių verčių reikia stacionarių taškų? Atsakymą į šį klausimą duoda Ferma teorema. Iš šios teoremos išplaukia, kad jei diferencijuojama funkcija tam tikru momentu turi ekstremumą (lokalų minimumą arba vietinį maksimumą), tai šis taškas yra stacionarus. Taigi funkcija dažnai paima didžiausią (mažiausią) reikšmę intervale X viename iš šio intervalo stacionarių taškų.

Be to, funkcija dažnai gali įgyti didžiausias ir mažiausias reikšmes taškuose, kuriuose nėra pirmosios šios funkcijos išvestinės, o pati funkcija yra apibrėžta.

Iš karto atsakykime į vieną dažniausių klausimų šia tema: „Ar visada įmanoma nustatyti didžiausią (mažiausią) funkcijos reikšmę“? Ne ne visada. Kartais intervalo X ribos sutampa su funkcijos apibrėžimo srities ribomis arba intervalas X yra begalinis. O kai kurios funkcijos begalybėje ir apibrėžimo srities ribose gali turėti ir be galo dideles, ir be galo mažas reikšmes. Tokiais atvejais nieko negalima pasakyti apie didžiausią ir mažiausią funkcijos reikšmę.

Aiškumo dėlei pateiksime grafinę iliustraciją. Pažvelkite į nuotraukas ir daug kas taps aiškiau.

Ant segmento

Pirmame paveikslėlyje funkcija užima didžiausias (max y) ir mažiausias (min y) vertes stacionariuose taškuose, esančiuose atkarpos viduje [-6;6].

Apsvarstykite atvejį, pavaizduotą antrame paveikslėlyje. Pakeiskime segmentą į . Šiame pavyzdyje mažiausia funkcijos reikšmė pasiekiama stacionariame taške, o didžiausia – taške, kurio abscisė atitinka dešiniąją intervalo ribą.

3 paveiksle atkarpos [-3;2] ribiniai taškai yra taškų, atitinkančių didžiausią ir mažiausią funkcijos reikšmę, abscisės.

Atviru intervalu

Ketvirtajame paveikslėlyje funkcija paima didžiausias (max y) ir mažiausias (min y) vertes stacionariuose taškuose, esančiuose atviro intervalo viduje (-6;6).

Intervale negalima daryti išvadų apie didžiausią reikšmę.

Begalybėje

Septintame paveikslėlyje pateiktame pavyzdyje funkcija įgauna didžiausią reikšmę (max y) stacionariame taške, kurio abscisė x=1, o mažiausia reikšmė (min y) pasiekiama dešinėje intervalo riboje. Esant minus begalybei, funkcijos reikšmės asimptotiškai artėja prie y=3.

Per intervalą funkcija nepasiekia nei mažiausios, nei didžiausios reikšmės. Artėjant x = 2 iš dešinės, funkcijos reikšmės linkusios atėmus begalybę (linija x = 2 yra vertikali asimptotė), o abscisei plius begalybei, funkcijos reikšmės asimptotiškai artėja prie y = 3. Šio pavyzdžio grafinė iliustracija parodyta 8 paveiksle.

Algoritmas, skirtas rasti didžiausią ir mažiausią ištisinės funkcijos reikšmes segmente.

Parašykime algoritmą, leidžiantį rasti didžiausią ir mažiausią segmento funkcijos reikšmes.

1. Surandame funkcijos apibrėžimo sritį ir patikriname, ar joje yra visas segmentas.
2. Randame visus taškus, kuriuose pirmoji išvestinė neegzistuoja ir kurie yra segmente (dažniausiai tokie taškai randami funkcijose su argumentu po modulio ženklu ir laipsnio funkcijose su trupmeniniu-racionaliuoju rodikliu). Jei tokių taškų nėra, pereikite prie kito punkto.
3. Nustatome visus stacionarius taškus, patenkančius į atkarpą. Norėdami tai padaryti, prilyginame jį nuliui, išsprendžiame gautą lygtį ir pasirenkame tinkamas šaknis. Jei nėra stacionarių taškų arba nė vienas iš jų nepatenka į atkarpą, pereikite prie kito taško.
4. Apskaičiuojame funkcijos reikšmes pasirinktuose stacionariuose taškuose (jei yra), taškuose, kuriuose nėra pirmosios išvestinės (jei yra), taip pat x=a ir x=b.
5. Iš gautų funkcijos reikšmių išrenkame didžiausią ir mažiausią – jos bus atitinkamai reikalingos didžiausios ir mažiausios funkcijos reikšmės.

Išanalizuokime pavyzdžio sprendimo algoritmą, kad surastume didžiausias ir mažiausias segmento funkcijos reikšmes.

Pavyzdys.

Raskite didžiausią ir mažiausią funkcijos reikšmę

• ant segmento;
• atkarpoje [-4;-1] .

Sprendimas.

Funkcijos apibrėžimo sritis yra visa realiųjų skaičių rinkinys, išskyrus nulį, tai yra. Abu segmentai patenka į apibrėžimo sritį.

Raskite funkcijos išvestinę, atsižvelgiant į:

Akivaizdu, kad funkcijos išvestinė egzistuoja visuose atkarpų taškuose ir [-4;-1].

Iš lygties nustatome stacionarius taškus. Vienintelė tikroji šaknis yra x=2. Šis stacionarus taškas patenka į pirmąjį segmentą.

Pirmuoju atveju apskaičiuojame funkcijos reikšmes atkarpos galuose ir stacionariame taške, ty x=1, x=2 ir x=4:

Todėl didžiausia funkcijos vertė pasiekiama, kai x=1, ir mažiausia reikšmė – ties x=2.

Antruoju atveju funkcijų reikšmes apskaičiuojame tik atkarpos [-4;-1] galuose (nes jame nėra nė vieno stacionaraus taško):

Sprendimas.

Pradėkime nuo funkcijos srities. Kvadratinis trinaris trupmenos vardiklyje neturi išnykti:

Nesunku patikrinti, ar visi problemos teiginio intervalai priklauso funkcijos apibrėžimo sričiai.

Išskirkime funkciją:

Akivaizdu, kad išvestinė egzistuoja visoje funkcijos apibrėžimo srityje.

Raskime stacionarius taškus. Išvestinė eina į nulį ties . Šis stacionarus taškas patenka į intervalus (-3;1] ir (-3;2).

Dabar kiekviename taške gautus rezultatus galite palyginti su funkcijos grafiku. Mėlynos punktyrinės linijos rodo asimptotes.

Šiuo metu galime baigti suradę didžiausias ir mažiausias funkcijos reikšmes. Šiame straipsnyje aptariami algoritmai leidžia pasiekti rezultatų atliekant minimalius veiksmus. Tačiau gali būti naudinga pirmiausia nustatyti funkcijos didėjimo ir mažėjimo intervalus ir tik po to daryti išvadas apie didžiausias ir mažiausias funkcijos reikšmes bet kuriame intervale. Tai suteikia aiškesnį vaizdą ir tikslesnį rezultatų pagrindimą.

Apibrėžimas3 . 3 Tegul yra tam tikra funkcija, jos apibrėžimo sritis ir tam tikras (atviras) intervalas (galbūt su ir (arba) ) 7 . Pavadinkime funkciją nuolatinis intervale, jei tęstinis bet kuriame taške, tai yra, bet kuriame taške (sutrumpinta forma:

Leiskite dabar būti (uždaras) segmentas . Pavadinkime funkciją ištisinis segmente, jei ištisinis intervale, ištisinis taške dešinėje ir ištisinis kairėje taške, tai yra

Pavyzdys3 . 13 Apsvarstykite funkciją (Heaviside funkcija) segmente , . Tada atkarpoje jis yra ištisinis (nepaisant to, kad taške jis turi pirmos rūšies pertrūkį).

3.15 pav. Heaviside funkcijos grafikas

Panašus apibrėžimas gali būti pateiktas ir formos pusiniams intervalams, įskaitant atvejus ir . Tačiau galime apibendrinti šį apibrėžimą savavališko pogrupio atveju taip. Pirmiausia pristatykime koncepciją sukeltasį bazes: tegul yra pagrindas, kurio visos galūnės turi netuščias sankirtas su . Pažymėkime ir apsvarstykime visų aibę. Tada nesunku patikrinti, ar rinkinys bus pagrindas. Taigi pagrindams , ir , kur , ir yra nepunktūruotų dvipusių (atitinkamai kairiųjų, dešiniųjų) taško apylinkių pagrindai (jų apibrėžimą žr. dabartinio skyriaus pradžioje).

Apibrėžimas3 . 4 Pavadinkime funkciją nenutrūkstamas filmavimo aikštelėje, Jei

Nesunku pastebėti, kad tada ir šis apibrėžimas sutampa su aukščiau pateiktais konkrečiai intervalui ir segmentui.

Prisiminkite, kad visos elementarios funkcijos yra tolydžios visuose jų apibrėžimo sričių taškuose, todėl tolydžios bet kuriuose intervaluose ir segmentuose, esančiuose jų apibrėžimo srityse.

Kadangi intervalo ir atkarpos tęstinumas apibrėžiamas taškiškai, galioja teorema, kuri yra tiesioginė 3.1 teoremos pasekmė:

Teorema3 . 5 Leisti Ir -- funkcijos ir - intervalas arba segmentas, esantis . Leisti Ir tęstinis už . Tada funkcijos , , tęstinis už . Jei papildomai visų akivaizdoje , tada funkcija taip pat nuolat veikia .

Iš šios teoremos, kaip ir iš 3.1 teoremos – 3.3 teiginio, išplaukia toks teiginys:

Pasiūlyti3 . 4 Krūva visos funkcijos tęsiasi intervale arba segmente -- tai linijinė erdvė:

Sudėtingesnė tolydžios funkcijos savybė išreiškiama tokia teorema.

Teorema3 . 6 (apie tolydžios funkcijos šaknį) Tegul funkcija ištisinis segmente , ir Ir -- skirtingų ženklų skaičius. (Tikslumui darysime prielaidą , A .) Tada yra bent viena tokia reikšmė , Ką (tai yra, yra bent viena šaknis lygtys ).

Įrodymas. Pažvelkime į segmento vidurį. Tada yra arba, arba, arba. Pirmuoju atveju randama šaknis: tai yra . Likusiais dviem atvejais apsvarstykite tą segmento dalį, kurios galuose funkcija įgauna skirtingų ženklų reikšmes: atveju arba atveju . Pasirinktą atkarpos pusę pažymime ir jai taikome tą pačią procedūrą: padaliname į dvi dalis ir , kur , ir randame . Tuo atveju, jei rasta šaknis; tuo atveju, jei toliau nagrinėjame segmentą , tuo atveju - segmentas ir tt

3.16 pav. Iš eilės atkarpos dalybos per pusę

Gauname, kad arba tam tikru žingsniu bus rasta šaknis, arba bus sukurta įdėtų segmentų sistema

kuriame kiekvienas paskesnis segmentas yra perpus ilgesnis nei ankstesnis. Seka nemažėjanti ir apribota iš viršaus (pavyzdžiui, skaičiumi); todėl (pagal 2.13 teoremą) ji turi ribą. Pasekmė - nedidėjantis ir apribotas žemiau (pavyzdžiui, skaičiumi ); tai reiškia, kad yra riba. Kadangi atkarpų ilgiai sudaro mažėjančią geometrinę progresiją (su vardikliu), jie linkę į 0 ir , tai yra . Padėkime dabar. Tada

Ir

kadangi funkcija yra nuolatinė. Tačiau, konstruojant sekas ir , ir , kad teorema pereinant prie ribos nelygybėje (2.7 teorema), ir , tai yra, ir . Tai reiškia, kad , ir yra lygties šaknis.

Pavyzdys3 . 14 Apsvarstykite funkciją segmente. Kadangi ir yra skirtingų ženklų skaičiai, funkcija tam tikru intervalo tašku virsta 0. Tai reiškia, kad lygtis turi šaknį.

3.17 pav.. Grafinis lygties šaknies pavaizdavimas

Įrodyta teorema iš tikrųjų suteikia mums būdą rasti šaknį, bent jau apytikslę, bet kokiu iš anksto nurodytu tikslumo laipsniu. Tai yra atkarpos padalijimo per pusę būdas, aprašytas teoremos įrodyme. Su šiuo ir kitais efektyvesniais apytiksliai šaknies radimo būdais susipažinsime toliau, išnagrinėję darinio sampratą ir savybes.

Atkreipkite dėmesį, kad teorema nesako, kad jei tenkinamos jos sąlygos, tada šaknis yra unikali. Kaip parodyta toliau pateiktame paveikslėlyje, gali būti daugiau nei viena šaknis (paveiksle yra 3).

3.18 pav. Kelios funkcijos šaknys, kurios segmento galuose ima skirtingų ženklų reikšmes

Tačiau jei funkcija monotoniškai didėja arba monotoniškai mažėja segmente, kurio galuose ji ima skirtingų ženklų reikšmes, tada šaknis yra unikali, nes griežtai monotoniška funkcija kiekvieną savo reikšmę įgauna tiksliai viename taške. , įskaitant reikšmę 0.

3.19 pav. Monotoninė funkcija negali turėti daugiau nei vieną šaknį

Tiesioginė teoremos pasekmė tolydžios funkcijos šaknyje yra sekanti teorema, kuri pati savaime yra labai svarbi matematinėje analizėje.

Teorema3 . 7 (apie tarpinę nuolatinės funkcijos reikšmę) Tegul funkcija ištisinis segmente Ir (tikslumui manysime, kad ). Leisti - tarp jų yra skaičius Ir . Tada yra toks punktas , Ką .

3.20 pav. Nepertraukiama funkcija įgauna bet kokią tarpinę reikšmę

Įrodymas. Apsvarstykite pagalbininko funkciją , Kur . Tada Ir . Funkcija akivaizdžiai yra ištisinė, o pagal ankstesnę teoremą yra taškas, kad . Tačiau ši lygybė reiškia tai.

Atminkite, kad jei funkcija nėra ištisinė, ji gali užimti ne visas tarpines reikšmes. Pavyzdžiui, funkcija Heaviside (žr. 3.13 pavyzdį) paima reikšmes, , bet niekur, įskaitant intervalą, neužima, tarkime, tarpinės reikšmės. Faktas yra tas, kad Heaviside funkcija turi pertrūkį taške, kuris yra tiksliai intervale.

Norėdami toliau tirti intervale ištisinių funkcijų savybes, mums reikės šios subtilios realiųjų skaičių sistemos savybės (ją jau minėjome 2 skyriuje, siejant su teorema apie monotoniškai didėjančios ribinės funkcijos ribą): bet kuri toliau apribota aibė (tai yra tokia, kad visiems ir kai kuriems; skaičius vadinamas apatinis kraštas rinkiniai) yra tikslus apatinis kraštas, tai yra, didžiausias iš skaičių toks, kad visiems . Panašiai, jei aibė yra ribojama aukščiau, tada ji turi tiksli viršutinė riba: tai mažiausias iš viršutiniai veidai(už kurį visiems).

3.21 pav. Apribotos aibės apatinė ir viršutinė ribos

Jei , tada yra nedidėjanti taškų seka, kuri linkusi . Tuo pačiu būdu, jei , tada yra nemažėjanti taškų seka, kuri linkusi į .

Jei taškas priklauso aibei, tai jis yra mažiausias šios aibės elementas: ; panašiai, jei , Tai.

Be to, toliau mums reikės šių dalykų

Lemma3 . 1 Leisti -- nepertraukiama funkcija segmente , ir daugelis tuos taškus , kuriame (arba , arba ) nėra tuščias. Tada gausiai yra mažiausia vertė , toks visų akivaizdoje .

3.22 pav. Mažiausias argumentas, kuriam esant funkcija įgauna nurodytą reikšmę

Įrodymas. Kadangi tai yra ribota aibė (ji yra segmento dalis), ji turi infimumą. Tada egzistuoja nedidėjanti seka , Tokia, kad už . Be to, pagal rinkinio apibrėžimą. Todėl pereidami prie ribos, viena vertus, gauname,

ir, kita vertus, dėl funkcijos tęstinumo,

Tai reiškia , kad taškas priklauso rinkiniui ir .

Tuo atveju, kai aibė apibrėžiama nelygybe, mes turime visiems ir teoremą pereinant prie ribos nelygybėje gauname

iš kur , o tai reiškia, kad ir . Panašiai nelygybės atveju perėjimas prie ribos nelygybėje duoda

iš kur ir.

Teorema3 . 8 (apie tolydžios funkcijos ribą) Tegul funkcija ištisinis segmente . Tada ribojamas iki , tai yra, yra tokia konstanta , Ką visų akivaizdoje .

3.23 pav. Atkarpoje ištisinė funkcija yra ribojama

Įrodymas. Tarkime priešingai: tegul neapsiriboja, pavyzdžiui, iš viršaus. Tada visi rinkiniai , , , nėra tušti. Pagal ankstesnę lemą, kiekviena iš šių rinkinių turi mažiausią reikšmę , . Parodykime tai

tikrai, . Jei bet kuris taškas iš , pavyzdžiui, yra tarp ir , Tada

tai yra tarpinė reikšmė tarp ir . Tai reiškia, kad pagal teoremą apie tarpinę nuolatinės funkcijos reikšmę egzistuoja taškas, kuriame , Ir. Tačiau, priešingai nei manoma, kad - mažiausia rinkinio vertė. Iš to išplaukia, kad visiems.

Lygiai taip pat toliau įrodyta, kad visiems , visiems ir tt Taigi, yra didėjanti seka, kurią riboja skaičius . Todėl jis egzistuoja. Iš funkcijos tęstinumo matyti, kad yra , Bet , todėl nėra jokių apribojimų. Gautas prieštaravimas įrodo, kad funkcija yra ribojama aukščiau.

Panašiai įrodoma, kad ji yra ribojama iš apačios, o tai reiškia teoremos teiginį.

Akivaizdu, kad teoremos sąlygų susilpninti neįmanoma: jei funkcija nėra tolydi, tai ji neturi būti apribota intervalu (pavyzdžiu pateikiame funkciją

segmente. Ši funkcija neapsiriboja intervalu, nes turi antrojo tipo nutrūkimo tašką, adresu . Taip pat neįmanoma teoremos sąlygoje segmento pakeisti intervalu ar pusintervalu: kaip pavyzdį, apsvarstykite tą pačią funkciją pusės intervale. Funkcija yra nenutrūkstama šiame pusės intervale, bet neapribota, nes .

Ieškodami geriausių konstantų, kurias galima naudoti norint apriboti funkciją iš viršaus ir apačios tam tikrame intervale, natūraliai kyla problemų, kaip rasti šio intervalo nuolatinės funkcijos minimumą ir maksimumą. Šios problemos sprendimo galimybė aprašyta tokia teorema.

Teorema3 . 9 (apie ekstremumo pasiekimą ištisine funkcija) Tegul funkcija ištisinis segmente . Tada yra taškas , toks visų akivaizdoje (tai yra -- minimalus taškas: ), ir yra prasmė , toks visų akivaizdoje (tai yra -- maksimalus taškas: ). Kitaip tariant, minimumas ir maksimumas 8 atkarpoje egzistuoja nuolatinės funkcijos reikšmės ir yra pasiekiamos kai kuriuose taškuose Ir šis segmentas.

3.24 pav. Atkarpoje nuolatinė funkcija pasiekia maksimumą ir minimumą

Įrodymas. Kadangi pagal ankstesnę teoremą funkcija yra ribojama aukščiau, tada yra tiksli viršutinė funkcijos verčių riba - skaičius . Taigi, rinkiniai , ,..., ,..., nėra tušti, o pagal ankstesnę lemą jose yra mažiausios reikšmės: , . Tai nesumažėja (šis teiginys įrodomas lygiai taip pat, kaip ir ankstesnėje teoremoje):

ir yra apriboti iš viršaus . Todėl pagal monotoninės apribotos sekos ribos teoremą egzistuoja riba Since , tada

teorema apie perėjimą prie nelygybės ribos, tai yra, . Bet su visais, įskaitant. Iš to paaiškėja, kad , tai yra, funkcijos maksimumas pasiekiamas taške .

Panašiai įrodomas minimalaus taško egzistavimas.

Šioje teoremoje, kaip ir ankstesnėje, neįmanoma susilpninti sąlygų: jei funkcija nėra tolydi, ji gali nepasiekti savo didžiausios arba minimalios reikšmės atkarpoje, net jei ji yra ribota. Pavyzdžiui, paimkime funkciją

segmente. Ši funkcija yra apribota intervalu (akivaizdu) ir , tačiau jokiame atkarpos taške ji neįgyja reikšmės 1 (atkreipkite dėmesį, kad , o ne 1). Faktas yra tas, kad ši funkcija turi pirmos rūšies nenutrūkstamumą taške, todėl riboje nėra lygi funkcijos reikšmei taške 0. Be to, ištisinė funkcija, apibrėžta intervale arba kitoje aibėje, kuri nėra uždaras segmentas (puse intervale, pusiau ašyje) taip pat negali priimti kraštutinių verčių. Kaip pavyzdį apsvarstykite intervalo funkciją. Akivaizdu, kad funkcija yra ištisinė ir kad ir , tačiau funkcija negauna nei reikšmės 0, nei reikšmės 1 jokiame intervalo taške. Taip pat apsvarstykime funkciją ant ašies veleno. Ši funkcija yra nuolatinė įjungta , didėja, taške įgyja mažiausią reikšmę 0, bet jokiame taške neįgyja didžiausios reikšmės (nors iš viršaus ją riboja skaičius ir

Apibrėžimas. Jei funkcija f(x) yra apibrėžtas intervale [ a, b], yra tęstinis kiekviename intervalo taške ( a, b), taške a ištisinis dešinėje, taške b yra tęstinis kairėje, tada sakome, kad funkcija f(x) ištisinis segmente [a, b].

Kitaip tariant, funkcija f(x) yra tęstinis intervale [ a, b], jei tenkinamos trys sąlygos:

1) "x 0 Î( a, b): f(x) = f(x 0);

2) f(x) = f(a);

3) f(x) = f(b).

Funkcijoms, kurios yra tolydžios intervale, atsižvelgiame į kai kurias savybes, kurias suformuluojame toliau pateiktų teoremų pavidalu, neatlikdami įrodymų.

1 teorema. Jei funkcija f(x) yra tęstinis intervale [ a, b], tada jis pasiekia savo minimalias ir didžiausias vertes šiame segmente.

Ši teorema teigia (1.15 pav.), kad atkarpoje [ a, b] yra toks punktas x 1 tai f(x 1) £ f(x) bet kuriam x iš [ a, b] ir kad yra prasmė x 2 (x 2 О[ a, b]) tokia, kad „ xÎ[ a, b] (f(x 2)³ f(x)).

Reikšmė f(x 1) yra didžiausia tam tikrai funkcijai [ a, b], A f(x 2) – mažiausias. Pažymime: f(x 1) = M, f(x 2) =m. Nuo f(x) nelygybė galioja: " xÎ[ a, b] m£ f(x) £ M, tada iš 1 teoremos gauname tokią išvadą.

Pasekmė. Jei funkcija f(x) yra tęstinis intervale, tada jis yra ribojamas su šiuo intervalu.

2 teorema. Jei funkcija f(x) yra tęstinis intervale [ a, b] ir segmento galuose paima skirtingų ženklų reikšmes, tada yra toks vidinis taškas x 0 segmentas [ a, b], kurioje funkcija virsta 0, t.y. $ x 0 Î ( a, b) (f(x 0) = 0).

Ši teorema teigia, kad funkcijos grafikas y = f(x), ištisinis intervalu [ a, b], kerta ašį Jautis bent kartą, jei reikšmės f(a) Ir f(b) turi priešingus požymius. Taigi, (1.16 pav.) f(a) > 0, f(b) < 0 и функция f(x) taškuose tampa 0 x 1 , x 2 , x 3 .

3 teorema. Tegul funkcija f(x) yra tęstinis intervale [ a, b], f(a) = A, f(b) = B Ir A¹ B. (1.17 pav.). Tada už bet kokį skaičių C, įterptas tarp skaičių A Ir B, yra toks vidinis taškas x 0 segmentas [ a, b], Ką f(x 0) = C.

Pasekmė. Jei funkcija f(x) yra tęstinis intervale [ a, b], m– mažiausia vertė f(x), M– didžiausia funkcijos vertė f(x) segmente [ a, b], tada funkcija (bent kartą) įgauna bet kokią reikšmę m, sudaryta tarp m Ir M, todėl segmentas [ m, M] yra visų funkcijų reikšmių rinkinys f(x) segmente [ a, b].

Atkreipkite dėmesį, kad jei funkcija yra ištisinė intervale ( a, b) arba yra segmente [ a, b] nenutrūkstamumo taškai, tada 1, 2, 3 teoremos tokiai funkcijai nustoja būti teisingos.

Pabaigoje apsvarstykite teoremą apie atvirkštinės funkcijos egzistavimą.

4 teorema. Leisti f(x) yra nuolatinis intervale X, padidėja (arba sumažėja) X ir turi verčių diapazoną Y. Tada dėl funkcijos y = f(x) yra atvirkštinė funkcija x= j(y), apibrėžtas intervale Y, nuolatinis ir didėjantis (arba mažėjantis). Y su daugybe reikšmių X.

komentuoti. Tegul funkcija x= j(y) yra atvirkštinė funkcija f(x). Kadangi argumentas dažniausiai žymimas x, o funkcija per y, tada atvirkštinę funkciją įrašome formoje y =j(x).

1 pavyzdys. Funkcija y = x 2 (1.8 pav., a) rinkinyje X= }