Dviejų stačiakampių impulsų spektras. Stačiakampių impulsų sekos spektrinė sudėtis skirtingais darbo ciklais
Literatūra: [L.1], 40 p
Kaip pavyzdį pateikiame Furjė serijos išplėtimą periodinės stačiakampių impulsų sekos su amplitude, trukme ir pasikartojimo periodu, simetriškai nuliui, t.y.
 , (2.10)
, (2.10)
Čia 
Išplėtus tokį signalą į Furjė seriją gaunama
 , (2.11)
, (2.11)
kur yra darbo ciklas.
Norėdami supaprastinti žymėjimą, galite įvesti užrašą
 , (2.12)
, (2.12)
Tada (2.11) bus parašytas taip
 , (2.13)
, (2.13)
Fig. 2.3 parodyta stačiakampių impulsų seka. Sekos spektras, kaip ir bet kuris kitas periodinis signalas, yra atskiro (linijinio) pobūdžio.
Spektro gaubtinė (2.3 pav., b) yra proporcinga  . Atstumas išilgai dažnio ašies tarp dviejų gretimų spektro komponentų yra , o tarp dviejų nulių verčių (spektro skilties plotis) yra . Harmoninių komponentų skaičius vienoje skiltyje, įskaitant nulinę reikšmę paveikslo dešinėje, yra , kur ženklas reiškia apvalinimą iki artimiausio sveikojo skaičiaus, mažesnis (jei darbo ciklas yra trupmeninis skaičius) arba (jei darbo ciklas yra sveikasis skaičius). Kai laikotarpis didėja, pagrindinis dažnis
. Atstumas išilgai dažnio ašies tarp dviejų gretimų spektro komponentų yra , o tarp dviejų nulių verčių (spektro skilties plotis) yra . Harmoninių komponentų skaičius vienoje skiltyje, įskaitant nulinę reikšmę paveikslo dešinėje, yra , kur ženklas reiškia apvalinimą iki artimiausio sveikojo skaičiaus, mažesnis (jei darbo ciklas yra trupmeninis skaičius) arba (jei darbo ciklas yra sveikasis skaičius). Kai laikotarpis didėja, pagrindinis dažnis  mažėja, diagramoje esantys spektriniai komponentai suartėja, harmonikų amplitudės taip pat mažėja. Tokiu atveju išsaugoma voko forma.
mažėja, diagramoje esantys spektriniai komponentai suartėja, harmonikų amplitudės taip pat mažėja. Tokiu atveju išsaugoma voko forma.




Sprendžiant praktines spektrinės analizės problemas, vietoj kampinių dažnių naudojami cikliniai dažniai  , matuojamas hercais. Akivaizdu, kad diagramoje atstumas tarp gretimų harmonikų bus , o vienos spektro skilties plotis bus . Šios reikšmės diagramoje pateikiamos skliausteliuose.
, matuojamas hercais. Akivaizdu, kad diagramoje atstumas tarp gretimų harmonikų bus , o vienos spektro skilties plotis bus . Šios reikšmės diagramoje pateikiamos skliausteliuose.
Praktinėje radijo inžinerijoje dažniausiai vietoj spektrinio vaizdavimo (2.3 pav., b) naudojamos amplitudės ir fazių spektrų spektrinės diagramos. Stačiakampių impulsų sekos amplitudės spektras parodytas fig. 2.3, c.
Akivaizdu, kad amplitudės spektro gaubtas yra proporcingas  .
.
Kalbant apie fazių spektrą (2.3 pav., d), manoma, kad pradinės harmoninių komponentų fazės staigiai keičiasi dydžiu -π kai pasikeičia voko ženklas nuo kπ/q. Laikoma, kad pirmosios skilties harmonikų pradinės fazės yra lygios nuliui. Tada bus pradinės antrojo skilties harmonikų fazės φ = -π , trečiasis žiedlapis φ = -2π ir tt
Panagrinėkime kitą Furjė serijos signalo atvaizdavimą. Norėdami tai padaryti, naudojame Eilerio formulę
 .
.
Pagal šią formulę signalo išplėtimo į Furjė seriją k-oji komponentė (2.9) gali būti pavaizduota taip
 ;
;  . (2.15)
. (2.15)
Čia dydžiai ir yra sudėtingi ir reiškia kompleksines spektro komponentų amplitudes. Tada serija
Furjė (2.8), atsižvelgiant į (2.14), bus tokia forma
 , (2.16)
, (2.16)
 , (2.17)
, (2.17)
Nesunku patikrinti, ar išplėtimas (2.16) atliktas pagal pagrindines funkcijas  , kurie taip pat yra stačiakampiai intervale
, kurie taip pat yra stačiakampiai intervale  , t.y.
, t.y.

Išraiška (2.16) yra sudėtinga forma Furjė serija, kuri tęsiasi iki neigiamų dažnių. Kiekiai ir  , kur žymi kompleksinį kiekio konjugatą, vadinami kompleksinės amplitudės spektras Nes yra sudėtingas dydis, iš (2.15) išplaukia, kad
, kur žymi kompleksinį kiekio konjugatą, vadinami kompleksinės amplitudės spektras Nes yra sudėtingas dydis, iš (2.15) išplaukia, kad
 Ir
Ir  .
.
Tada visuma sudaro amplitudės spektrą, o visuma sudaro signalo fazių spektrą.

Fig. 2.4 paveiksle parodyta aukščiau aptartų stačiakampių impulsų sekos spektro spektrinė diagrama, pavaizduota sudėtinga Furjė serija

Spektras taip pat turi linijinį pobūdį, tačiau skirtingai nuo anksčiau svarstytų spektrų, jis nustatomas tiek teigiamų, tiek neigiamų dažnių srityje. Kadangi yra lyginė argumento funkcija, spektrinė diagrama yra simetriška nuliui.
Remdamiesi (2.15), galime nustatyti atitiktį tarp koeficientų ir plėtimosi (2.3). Nes
 Ir
Ir  ,
,
tada kaip rezultatas gauname
 . (2.18)
. (2.18)
Išraiškos (2.5) ir (2.18) leidžia rasti reikšmes atliekant praktinius skaičiavimus.
Pateikiame Furjė serijos sudėtingos formos geometrinę interpretaciją. Pasirinkime k-tą signalo spektro komponentą. Sudėtingoje formoje k-asis komponentas apibūdinamas formule
kur ir nustatomi išraiškomis (2.15).
Sudėtingoje plokštumoje kiekvienas (2.19) terminas yra pavaizduotas kaip ilgio vektorius  , pasuktas kampu ir tikrosios ašies atžvilgiu bei besisukantis priešingomis kryptimis su dažniu (2.5 pav.).
, pasuktas kampu ir tikrosios ašies atžvilgiu bei besisukantis priešingomis kryptimis su dažniu (2.5 pav.).
Akivaizdu, kad šių vektorių suma suteikia vektorių, esantį ant tikrosios ašies, kurio ilgis yra . Tačiau šis vektorius atitinka harmoninį komponentą


Kalbant apie vektorių projekcijas į įsivaizduojamą ašį, šios projekcijos yra vienodo ilgio, bet priešingų krypčių ir sumuojamos iki nulio. Tai reiškia, kad signalai, pateikti sudėtinga forma (2.16), iš tikrųjų yra tikri signalai. Kitaip tariant, Furjė serijos sudėtinga forma yra matematinės abstrakcija, kuri yra labai patogi sprendžiant daugybę spektrinės analizės problemų. Todėl kartais vadinamas trigonometrine Furjė eilute apibrėžtu spektru fizinis spektras, o Furjė serijos sudėtinga forma yra matematinis spektras.
Ir pabaigai apsvarstysime energijos ir galios pasiskirstymo periodinio signalo spektre klausimą. Norėdami tai padaryti, naudojame Parseval lygybę (1,42). Kai signalas išplečiamas į trigonometrinę Furjė eilutę, išraiška (1.42) įgauna formą
 .
.
DC energija
 ,
,
ir k-osios harmonikos energija
 .
.
Tada signalo energija
 . (2.20)
. (2.20)
Nes vidutinė signalo galia
 ,
,
tada atsižvelgiant į (2.18)
 . (2.21)
. (2.21)
Kai signalas išplečiamas į sudėtingą Furjė eilutę, išraiška (1.42) įgauna formą
 ,
,
Kur  - k-osios harmonikos energija.
- k-osios harmonikos energija.
Signalo energija šiuo atveju
 ,
,
ir jo vidutinė galia
 .
.
Iš aukščiau pateiktų išraiškų išplaukia, kad matematinio spektro k-osios spektrinės dedamosios energija arba vidutinė galia yra perpus mažesnė už atitinkamo fizikinio spektro spektrinio komponento energiją arba galią. Taip yra dėl to, kad fizikinis spektras yra tolygiai paskirstytas tarp matematinio spektro.
| -τ ir /2 |
| τ ir /2 |
| T |
| t |
| U 0 |
| S(t) |
Užduotis Nr.1, grupė RI – 210701
Periodinės stačiakampių impulsų sekos plačiai naudojamos elektroninėje įrangoje įvairioms reikmėms. Šiuo atveju ryšys tarp impulso trukmės τ ir virpesių periodo T gali labai skirtis. Pavyzdžiui, vibracijos, kurios sukelia laikrodžių generatoriai, kurie nustato kompiuterio veikimo „tempą“, pasižymi palyginamomis τ ir reikšmėmis T, o radare naudojami impulsai gali būti šimtus kartų trumpesni už laikotarpį. Požiūris T/τ vadinamas pulso darbo ciklas, ir atvirkštinė reikšmė (τ/ T) - užpildymo koeficientas.
Ryžiai. 6. Stačiakampių impulsų seka (a) ir Furjė eilutės koeficientai (b)
Apsvarstykite stačiakampių impulsų seką su amplitude A, trukmė τ ir vėlesnės su tašku T(6 pav., A). Laiko skaičiavimo pradžią parinksime taip, kaip parodyta paveikslėlyje, tai yra, kad impulsas būtų simetriškas nulinės žymos atžvilgiu, ir apskaičiuokime Furjė eilutės (1) koeficientus. Nuo funkcijos s(t) su šia ašių padėtimi pasirodo lygi, viskas b n yra lygūs nuliui, ir už a n mes gauname:
Furjė serija, skirta stačiakampių impulsų sekai, yra tokia:
 (6)
(6)
Furjė serijos koeficientų reikšmės, apskaičiuotos pagal (5) formules, yra pavaizduotos spektrinėje diagramoje, parodytoje Fig. 6, b.
Šansai a n gali būti susietas su funkcija  . Iš tiesų, jie bus proporcingi (su koeficientu
. Iš tiesų, jie bus proporcingi (su koeficientu  ) funkcijos reikšmės
) funkcijos reikšmės  su argumentais, atitinkančiais harmoninius dažnius. Tai galima pamatyti, jei išraiška (5) perrašoma taip:
su argumentais, atitinkančiais harmoninius dažnius. Tai galima pamatyti, jei išraiška (5) perrašoma taip:
 (7)
(7)
Taigi tokia funkcija kaip  yra vokas už koeficientus Furjė išplėtimai stačiakampių impulsų sekos (žr. 6 pav., b). Apgaubiųjų nulių padėtis dažnio ašyje f galima rasti iš būklės
yra vokas už koeficientus Furjė išplėtimai stačiakampių impulsų sekos (žr. 6 pav., b). Apgaubiųjų nulių padėtis dažnio ašyje f galima rasti iš būklės  arba
arba  , Kur. Pirmą kartą voko dažnis pasiekia nulį f= 1/τ (arba ω = 2π/τ). Toliau voko nuliai kartojami ties f= 2/τ, 3/τ ir tt Šie dažniai gali sutapti (su sveikų skaičių darbo ciklais) su bet kokių spektro harmonikų dažniais, ir šie dažnio komponentai iš Furjė serijos išnyks. Jei darbo ciklas yra sveikasis skaičius, laikotarpis T tiksliai impulso trukmės kartotinis. Tada tarp dviejų gaubto nulių bus spektro harmonikų kiekis q-
1.
, Kur. Pirmą kartą voko dažnis pasiekia nulį f= 1/τ (arba ω = 2π/τ). Toliau voko nuliai kartojami ties f= 2/τ, 3/τ ir tt Šie dažniai gali sutapti (su sveikų skaičių darbo ciklais) su bet kokių spektro harmonikų dažniais, ir šie dažnio komponentai iš Furjė serijos išnyks. Jei darbo ciklas yra sveikasis skaičius, laikotarpis T tiksliai impulso trukmės kartotinis. Tada tarp dviejų gaubto nulių bus spektro harmonikų kiekis q-
1.
1 lentelėje parodyta, kaip impulsų parametrai yra susieti pagal laiką ir dažnį. 2. Ilgėjant laikotarpiui T spektrinėje diagramoje esančios harmonikos suartėja (spektras tampa „storesnis“). Tačiau pakeitus tik periodą, amplitudės spektro gaubto forma nekeičiama. Apgaubos raida (jo nulių poslinkis) priklauso nuo impulso trukmės. Čia parodyta stačiakampių impulsų, kurių impulsų trukmė ir periodai skiriasi, sekų amplitudės spektrinių diagramų raida. Spektrinių diagramų ordinačių ašys rodo harmoninių amplitudių santykines reikšmes:  Jie apskaičiuojami pagal formules:
Jie apskaičiuojami pagal formules:
 (8)
(8)
2 lentelė. Stačiakampių impulsų sekų oscilogramos ir spektrogramos

2.5. Chaotiškų (triukšmo) virpesių spektrai
Chaotiškas svyravimas s(t) - Tai atsitiktinis procesas. Kiekvienas jo įgyvendinimas pastoviomis sąlygomis nesikartoja ir yra unikalus. Elektronikoje chaotiški svyravimai siejami su triukšmo- srovių ir įtampų svyravimai, kurie kinta atsitiktinai dėl atsitiktinio krūvininkų judėjimo. Šiame kontekste chaotiškos ir triukšmingos vibracijos laikomos sinonimais.
Ryžiai. 7. Vidutinės kvadratinės triukšmo įtampos matavimo blokinė schema
Triukšmo svyravimas galima apibūdinti dažnio vaizdavimu: jis yra susietas su tam tikra spektrine charakteristika, o atsitiktiniam procesui yra tęstinis. Pateikiami chaotiškų virpesių spektrinio skaidymo teoriniai pagrindai. Nesigilindami į griežtą teoriją, paaiškinsime statistinių parametrų eksperimentinio tyrimo metodiką triukšmo įtampa s(t) pagal schemą, parodytą pav. 8.
R  yra. 8. Triukšmo įtampos intensyvumo spektrinio tankio matavimo schema
yra. 8. Triukšmo įtampos intensyvumo spektrinio tankio matavimo schema
Praleiskime triukšmo įtampą s(t) per filtrą, kuris išskiria virpesių energiją siauroje juostoje  artimas dažnis f. Jei sąlyga yra įvykdyta
artimas dažnis f. Jei sąlyga yra įvykdyta  <<
f filtro išėjimo virpesiai bus panašūs į sinusoidę su dažniu f. Tačiau šio sinusoido amplitudė ir fazė gali keistis chaotiškai. Su mažėjančiu filtro pralaidumu
<<
f filtro išėjimo virpesiai bus panašūs į sinusoidę su dažniu f. Tačiau šio sinusoido amplitudė ir fazė gali keistis chaotiškai. Su mažėjančiu filtro pralaidumu  išėjimo svyravimo forma vis labiau artėja prie sinusoidės. Jo amplitudė mažėja, tačiau vidutinės kvadratinės įtampos, praeinančios per filtrą, santykis (
išėjimo svyravimo forma vis labiau artėja prie sinusoidės. Jo amplitudė mažėja, tačiau vidutinės kvadratinės įtampos, praeinančios per filtrą, santykis (  ), į pralaidumą
), į pralaidumą  išlieka baigtinis ir, nuosekliai mažėjant juostai, siekia tam tikrą ribą W(f):
išlieka baigtinis ir, nuosekliai mažėjant juostai, siekia tam tikrą ribą W(f):
Ribinė vertė W(f) yra vadinami spektrinio intensyvumo tankis procesas s(t).
Jis lygus vidutiniam harmoninių komponentų intensyvumui dažnio ašies vieneto intervale. Matuojant W(f) naudokite siauros juostos derinamą filtrą, kurį galima sureguliuoti bet kokiu dažniu tam tikrame matavimo diapazone. Triukšmo įtampa, einanti per filtrą, aptinkama kvadratiniu būdu ir suvidurkinama (integruota). Rezultatas yra vidutinis kvadratas:  . Toliau palei žinomą filtro juostą
. Toliau palei žinomą filtro juostą  apskaičiuoti W(f).
Visas proceso intensyvumas- vidutinis kvadratas
apskaičiuoti W(f).
Visas proceso intensyvumas- vidutinis kvadratas  - randama integruojant visų dažnių triukšmo spektrinius komponentus:
- randama integruojant visų dažnių triukšmo spektrinius komponentus:
 (10)
(10)
Norėdami pasiruošti darbui, turėtumėte perskaityti visą šį vadovą. Išsamesnę informaciją laboratorinių darbų tema rasite knygos skyriuje „Elektrinių virpesių dažniniai spektrai, spektrinė analizė“.
Periodinė stačiakampių vaizdo impulsų seka yra moduliavimo funkcija, skirta formuoti periodinę stačiakampių radijo impulsų (PPRP) seką, kuri yra zondavimo signalai, skirti aptikti ir išmatuoti judančių taikinių koordinates. Todėl naudojant moduliavimo funkcijos spektrą (PPVI) galima palyginti paprastai ir greitai nustatyti zondavimo signalo (PPVI) spektrą. Kai zondavimo signalas atsispindi nuo judančio taikinio, pasikeičia nešančiosios bangos harmoninio spektro dažniai (Doplerio efektas). Dėl to galima atpažinti nuo judančio taikinio atsispindintį naudingą signalą trukdančių (interferencinių) vibracijų, atsispindinčių nuo nejudančių objektų (vietinių objektų) arba lėtai judančių objektų (meteorologinių darinių, paukščių pulkų ir kt.), fone. .
PPPVI (1.42 pav.) – tai pavienių stačiakampių vaizdo impulsų, sekančių vienas kitą vienodais laiko intervalais, rinkinys. Analitinė signalo išraiška.
kur yra impulso amplitudė; – pulso trukmė; – pulso pasikartojimo periodas; – pulso pasikartojimo dažnis, ; – darbo ciklas.
Norint apskaičiuoti periodinės impulsų sekos spektrinę sudėtį, naudojama Furjė eilutė. Kai žinomi atskirų impulsų spektrai, sudarantys periodinę seką, galime naudoti ryšį tarp impulsų spektrinio tankio ir kompleksinių serijos amplitudių:
Vieno stačiakampio vaizdo impulso spektrinis tankis apibūdinamas formule
Naudodami ryšį tarp vieno impulso spektrinio tankio ir kompleksinių serijų amplitudių, randame
kur = 0; ± 1; ± 2; ...
Amplitudės-dažnio spektras (1.43 pav.) bus pavaizduotas komponentų rinkiniu:
šiuo atveju teigiamos reikšmės atitinka nulį pradinių fazių, o neigiamos reikšmės – pradines fazes, lygias .
Taigi, PPPVI analitinė išraiška bus lygi
Iš 1.43 pav. pateiktų grafikų analizės matyti:
· PPPVI spektras yra diskretus, susidedantis iš atskirų harmonikų su dažniu .
· AKM vokas keičiasi pagal įstatymus.
· Maksimali apgaubos reikšmė at yra lygi pastovios dedamosios reikšmei.
· Pradinės harmonikų fazės nelyginėse skiltyse yra lygios 0, lyginėse skiltyse .
· Harmonikų skaičius kiekvienoje skiltyje yra lygus .
Signalo spektro plotis esant 90 % signalo energijos
· Signalo bazė, todėl signalas paprastas.
Jei pakeisite impulsų trukmę ar jų pasikartojimo dažnį F(laikotarpis), tada pasikeis spektro ir jo ASF parametrai.
1.43 paveiksle parodytas signalo ir jo ASF pasikeitimo pavyzdys padvigubėjus impulso trukmei.
Periodinės stačiakampių vaizdo impulsų sekos ir jų ASF parametrai, T,. ir , T, parodytos 1.44 pav.
Iš pateiktų grafikų analizės matyti:
1. PPPVI su impulso trukme:
· Pareigos santykis q=4, todėl kiekvienoje skiltyje sutelktos 3 harmonikos;
· k-osios harmonikos dažnis;
· Signalo spektro plotis esant 90% energijos lygiui;
Pastovus komponentas yra lygus
2. PPPVI su impulso trukme:
· Pareigos santykis q= 2, todėl kiekvienoje skiltyje yra 1 harmonika;
· K-osios harmonikos dažnis išlieka nepakitęs;
· Signalo spektro plotis 90% jo energijos lygyje sumažėjo 2 kartus;
· Pastovus komponentas padidėjo 2 kartus.
Taigi galime daryti išvadą, kad didėjant impulso trukmei, ASF „suspaudžiamas“ išilgai ordinačių ašies (signalo spektro plotis mažėja), o spektrinių komponentų amplitudės didėja. Harmonikos dažniai nesikeičia.
1.44 pav. Pateikiamas signalo ir jo ASF pasikeitimo pavyzdys, kai pasikartojimo periodas padidėja 4 kartus (pasikartojimo dažnis sumažėja 4 kartus).
c) signalo spektro plotis 90% jo energijos lygyje nepasikeitė;
d) pastovioji dedamoji sumažėjo 4 kartus.
Taigi galime daryti išvadą, kad didėjant pasikartojimo periodui (sumažėjus pasikartojimo dažniui), ASF išilgai dažnio ašies atsiranda „suspaudimas“ (harmonikų amplitudės mažėja didėjant jų skaičiui kiekvienoje skiltyje). . Signalo spektro plotis nesikeičia. Tolesnis pasikartojimo dažnio sumažėjimas (pasikartojimo periodo padidėjimas) sukels (at ) harmonikų amplitudės sumažėjimą iki be galo mažų verčių. Tokiu atveju signalas pavirs vienu ir atitinkamai spektras taps tęstinis.
Ryšio teorijoje plačiai naudojamas spektrinis laiko funkcijų vaizdavimas. Elektros grandinių charakteristikų ir pranešimų perdavimo ryšio kanalais teoriniams ir eksperimentiniams tyrimams naudojami įvairių tipų signalai: harmoniniai virpesiai, pastovūs įtampos lygiai, stačiakampių ir radijo impulsų sekos ir kt. vieneto funkcija atlieka ypač svarbų vaidmenį teoriniuose elektros grandinių ir impulsinės funkcijos tyrimuose (Dirac funkcija). Nustatykime dažniausiai pasitaikančių tipinių signalų spektrus.
11.1 Stačiakampių impulsų sekos spektras
Tebūna periodinė stačiakampių impulsų seka su periodu T, impulso trukme t ir amplitudė A. Funkcijos, apibūdinančios impulsą segmente, analitinė išraiška turi tokią formą
 (11.1)
(11.1)
Periodinių impulsų sekos grafikas parodytas 11.1 pav.

11.1 pav
Ši funkcija yra lygi, nes jos grafikas yra simetriškas ordinatės atžvilgiu. Tada šių funkcijų Furjė koeficientai apskaičiuojami naudojant formules (KFT2), kur .

Skaičius reiškia vidutinę funkcijos reikšmę per laikotarpį ir vadinamas pastoviuoju komponentu. Dažnis vadinamas pagrindine arba pirmąja harmonika, o k dažniai vadinami aukštesnėmis harmonikomis, kur k = 2,3,4,...
Sukurkime nagrinėjamos stačiakampių impulsų sekos amplitudės spektrą. Kadangi funkcija yra periodinė, jos amplitudės spektras yra išklotas. Pažymėkime atstumu tarp bet kokių gretimų harmonikų. Akivaizdu, kad jis lygus . K-osios harmonikos amplitudė pagal (11.2) turi formą
 (11.3)
(11.3)
Raskime ryšį tarp periodo T ir impulso trukmės, kai k-osios harmonikos amplitudė tampa lygi nuliui.
A 2 ≈ 32 V, A 3 ≈ 15 V, A 4 ≈ 0, A 5 ≈ 6,36 V, A 6 ≈ 10,5 V, A 7 ≈ 6,36 V, A 8 ≈ 0, A 9 ≈ 4,95 V, A 6,37 V.
Skaičiavimo metu gautas amplitudės spektras parodytas 11.2 pav.

11.2 pav
Toks spektras vadinamas linijiniu arba diskrečiu spektru.
Spektrai q=8 ir q=16 buvo apskaičiuoti ir pavaizduoti panašiai. Jie parodyti atitinkamai 11.3 ir 11.4 paveiksluose.

11.3 pav

11.4 pav
Iš paveikslo matyti, kad kuo didesnis stačiakampių impulsų darbo ciklas, tuo mažesnė pirmosios harmonikos amplitudė, bet tuo lėčiau mažėja spektras.
11.2 Vieno stačiakampio impulso spektras
Panagrinėkime Ф (11.1) tuo atveju, kai T→∞, tai yra periodinė impulsų seka išsigimsta į vieną stačiakampį impulsą, kurio trukmė t u.
Šio impulso analitinė išraiška bus parašyta taip:
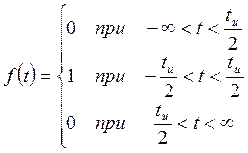
Šios funkcijos grafikas parodytas 11.5 pav.

11.5 pav
Tokiu atveju pirmosios harmonikos dažnis ir atstumas tarp harmonikų tampa lygus 0, todėl spektras iš diskrečiojo virsta ištisiniu, susidedančiu iš be galo daug spektrinių linijų, esančių be galo mažais atstumais viena nuo kitos. Toks spektras vadinamas nuolatiniu. Tai veda prie svarbiausios taisyklės: periodiniai signalai generuoja atskirus spektrus, o neperiodiniai – nuolatinius.
Stačiakampio vieno impulso spektrą galima rasti tiesiogiai iš tiesioginės Furjė transformacijos (10.1)
