خصائص الوظائف المستمرة في المقابلة

دعونا نفكر في بعض خصائص الدوال المستمرة على فترة زمنية. ونقدم هذه الخصائص دون دليل.

وظيفة ص = و(س)مُسَمًّى المستمر على الجزء [أ, ب]، إذا كانت متصلة في جميع النقاط الداخلية لهذا المقطع، وفي أطرافه، أي. في النقاط أو ب، مستمر على اليمين واليسار، على التوالي.

النظرية 1.دالة مستمرة على الفترة [ أ, ب]، على الأقل عند نقطة واحدة من هذا المقطع يأخذ القيمة الأكبر وعلى الأقل عند نقطة واحدة يأخذ القيمة الأصغر.

تنص النظرية على أنه إذا كانت الوظيفة ص = و(س)مستمرة على الفترة [ أ, ب]، ثم هناك نقطة واحدة على الأقل × 1 Î [ أ, ب] بحيث تكون قيمة الوظيفة و (خ)في هذه المرحلة ستكون الأكبر من بين جميع قيمها في هذا الجزء: و(س 1) ≥ و(خ). وبالمثل، هناك مثل هذه النقطة × 2، حيث تكون قيمة الدالة هي الأصغر بين جميع القيم الموجودة في المقطع: و(س 1) ≥ و(خ).

ومن الواضح أنه قد يكون هناك العديد من هذه النقاط، على سبيل المثال، يوضح الشكل أن الوظيفة و (خ)يأخذ أصغر قيمة عند نقطتين × 2و س 2 ".

تعليق. يمكن أن تصبح عبارة النظرية غير صحيحة إذا أخذنا في الاعتبار قيمة الدالة في الفترة ( أ, ب). في الواقع، إذا نظرنا إلى الوظيفة ص = سعلى (0، 2)، فهي مستمرة على هذا الفاصل، لكنها لا تصل إلى أكبر القيم فيها ولا إلى أصغرها: تصل إلى هذه القيم في نهايات الفاصل، لكن الأطراف لا تنتمي إلى المجال لدينا.

كما أن النظرية لم تعد صحيحة بالنسبة للدوال غير المتصلة. اعط مثالا.

عاقبة.إذا كانت الوظيفة و (خ)مستمر على [ أ, ب]، فهو يقتصر على هذا الجزء.

النظرية 2.دع الوظيفة ص = و(س)مستمرة على الفترة [ أ, ب] وفي نهايات هذا المقطع تأخذ قيم إشارات مختلفة، ثم هناك نقطة واحدة على الأقل داخل المقطع س = ج، حيث تصبح الدالة صفرًا: و(ج)= 0، حيث أ< C< b

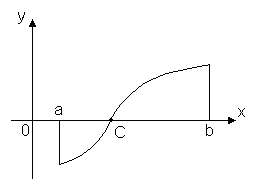
هذه النظرية لها معنى هندسي بسيط: إذا كانت نقاط الرسم البياني لدالة مستمرة ص = و(س)، المقابلة لنهايات المقطع [ أ, ب] تقع على جانبي المحور ثور، فإن هذا الرسم البياني يتقاطع مع المحور عند نقطة واحدة على الأقل من المقطع ثور. قد لا تحتوي الوظائف المتقطعة على هذه الخاصية.

هذه النظرية تعترف بالتعميم التالي.

النظرية 3 (نظرية القيمة المتوسطة).دع الوظيفة ص = و(س)مستمرة على الفترة [ أ, ب] و و(أ) = أ, و(ب) = ب. ثم لأي رقم ج، خلص بين أو ب، هناك مثل هذه النقطة داخل هذا الجزء جÎ [ أ, ب]، ماذا و(ج) = ج.

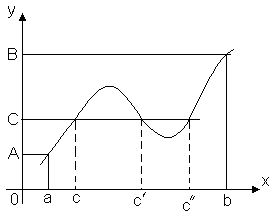
هذه النظرية واضحة هندسيا. النظر في الرسم البياني للوظيفة ص = و(س). يترك و(أ) = أ, و(ب) = ب. ثم أي خط مستقيم ص = ج، أين ج- أي رقم بين أو ب، سوف يتقاطع مع الرسم البياني للدالة عند نقطة واحدة على الأقل. ستكون حدود نقطة التقاطع هي تلك القيمة س = ج، الذي و(ج) = ج.

وبالتالي، فإن الدالة المستمرة، التي تنتقل من قيمة إلى أخرى، تمر بالضرورة عبر جميع القيم الوسيطة. بخاصة:

عاقبة.إذا كانت الوظيفة ص = و(س)متصلة خلال فترة معينة وتأخذ القيم الأكبر والأصغر، ثم في هذه الفترة تأخذ مرة واحدة على الأقل أي قيمة موجودة بين قيمها الأصغر والأكبر.

المشتقات وتطبيقاتها. تعريف المشتقات

دعونا نحصل على بعض الوظائف ص = و (س)،محددة على بعض الفاصل الزمني. لكل قيمة وسيطة سمن هذا الفاصل الدالة ص = و (س)له معنى معين.

خذ بعين الاعتبار قيمتين للوسيطة: الأولي س 0 وجديدة س.

اختلاف س – س 0 يسمى عن طريق زيادة الوسيطة xعند هذه النقطة س 0 ويشار إليه Δx. هكذا، Δس = س - س 0 (يمكن أن تكون زيادة الوسيطة موجبة أو سالبة). ومن هذه المساواة يترتب على ذلك س=س 0 +Δس، أي. تلقت القيمة الأولية للمتغير بعض الزيادة. ثم إذا كان عند هذه النقطة س 0 قيمة الدالة كانت و(س 0 ), ثم عند نقطة جديدة سسوف تأخذ الدالة القيمة و(س) = و(س 0 +Δس).

اختلاف ص – ذ 0 = و(س) - و(س 0 ) مُسَمًّى زيادة الوظيفة ص = و(س)عند هذه النقطة س 0 ويشار إليه بالرمز Δy. هكذا،

عادة القيمة الأولية للوسيطة س 0 يعتبر ثابتا، والقيمة الجديدة س- عامل. ثم ذ 0 = و(س 0 ) تبين أن تكون ثابتة، و ص = و(س)- عامل. الزيادات Δyو Δxستكون أيضًا متغيرات وتظهر الصيغة (1) ذلك ديهي وظيفة للمتغير Δx.

لنقم بإنشاء نسبة زيادة الدالة إلى زيادة الوسيطة

دعونا نجد الحد الأقصى لهذه النسبة عند Δx→0. إذا وجدت هذه النهاية، فإنها تسمى مشتقة هذه الدالة و (خ)عند هذه النقطة س 0 و تدل F "(س 0). لذا،

المشتقهذه الوظيفة ص = و(س)عند هذه النقطة س 0 يسمى حد نسبة زيادة الوظيفة Δ ذإلى زيادة الوسيطة Δ س، عندما يميل الأخير بشكل تعسفي إلى الصفر.

لاحظ أنه لنفس الوظيفة المشتق في نقاط مختلفة سيمكن أن تأخذ على قيم مختلفة، أي. يمكن اعتبار المشتق بمثابة وظيفة للحجة س. تم تعيين هذه الوظيفة F "(س)

يتم الإشارة إلى المشتق بالرموز F "(س)،ص"، . القيمة المحددة للمشتق عند س = أيُشار إليه بـ F "(أ) أو ذ "| س=أ.

عملية إيجاد مشتقة دالة و (خ)يسمى تمايز هذه الوظيفة.

للعثور مباشرة على المشتق حسب التعريف، يمكنك استخدام ما يلي: بحكم التجربة:

أمثلة.

المعنى الميكانيكي للمشتقات

ومن المعروف من الفيزياء أن قانون الحركة المنتظمة له الشكل ق = الخامس ر، أين س- المسار الذي سافر إلى لحظة الزمن ر, الخامس– سرعة الحركة المنتظمة .

ومع ذلك، لأن معظم الحركات التي تحدث في الطبيعة تكون متفاوتة، وبشكل عام السرعة، وبالتالي المسافة سسوف يعتمد على الوقت ر، أي. سوف تكون دالة للوقت.

إذن، لتتحرك نقطة مادية في خط مستقيم في اتجاه واحد وفقا للقانون ق = ق (ر).

دعونا نحتفل بنقطة معينة في الوقت المناسب ر 0 . عند هذه النقطة تكون النقطة قد اجتازت المسار ق = ق (ر 0 ). دعونا نحدد السرعة الخامسنقطة مادية في لحظة من الزمن ر 0 .

للقيام بذلك، دعونا نفكر في نقطة أخرى في الوقت المناسب ر 0 + Δ ر. وهو يتوافق مع المسار المسافر s =س(ر 0 + Δ ر). ثم على مدى فترة من الزمن Δ رلقد قطعت النقطة المسار Δs =س(ر 0 + Δ ر)–شارع).

دعونا ننظر في الموقف. ويسمى السرعة المتوسطة في الفترة الزمنية Δ ر. لا يمكن للسرعة المتوسطة أن تصف بدقة سرعة حركة نقطة ما في الوقت الحالي ر 0 (لأن الحركة غير متساوية). من أجل التعبير بشكل أكثر دقة عن هذه السرعة الحقيقية باستخدام متوسط ​​السرعة، عليك أن تأخذ فترة زمنية أقصر Δ ر.

إذن سرعة الحركة في لحظة معينة من الزمن ر 0 (السرعة اللحظية) هي الحد الأقصى لمتوسط ​​السرعة في الفترة من ر 0 ل ر 0 +Δ ر، عندما Δ ر→0:

,

أولئك. سرعة متفاوتةهذا هو مشتق المسافة المقطوعة بالنسبة للزمن.

المعنى الهندسي للمشتقات

دعونا نقدم أولاً تعريف مماس المنحنى عند نقطة معينة.

دعونا نحصل على منحنى ونقطة ثابتة عليه م 0(انظر الشكل) لننظر إلى نقطة أخرى مهذا المنحنى ورسم القاطع م 0 م. إذا كانت النقطة ميبدأ التحرك على طول المنحنى، وهذه النقطة م 0يبقى بلا حراك، ثم يغير القاطع موقعه. إذا، مع تقريب غير محدود للنقطة معلى طول منحنى إلى نقطة م 0على أي جانب يميل القاطع إلى احتلال موضع خط مستقيم معين م 0 ت، ثم على التوالي م 0 تيسمى المماس للمنحنى عند نقطة معينة م 0.

الذي - التي.، الظلإلى المنحنى عند نقطة معينة م 0يسمى الموضع الحدي للقاطع م 0 معندما نقطة ميميل على طول المنحنى إلى نقطة ما م 0.

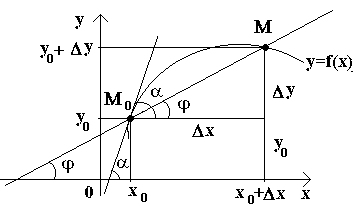
دعونا الآن نفكر في الدالة المستمرة ص = و (س)والمنحنى المقابل لهذه الوظيفة. في بعض القيمة X 0 وظيفة تأخذ القيمة ص 0 = و(س 0).هذه القيم س 0 و ذ 0 على المنحنى يتوافق مع نقطة م 0 (س 0 ؛ ص 0).دعونا نعطي الحجة × 0زيادة Δ X. تتوافق القيمة الجديدة للوسيطة مع القيمة المتزايدة للدالة ذ 0 +Δ ص=و(x 0 –Δ س). لقد حصلنا على هذه النقطة م (× 0+Δ س; ص 0+Δ ذ).دعونا نرسم القاطع م 0 موتدل على φ الزاوية التي يشكلها القاطع مع الاتجاه الموجب للمحور ثور. دعونا ننشئ علاقة ونلاحظ أن .

إذا الآن Δ س→0، ثم بسبب استمرارية الوظيفة Δ في→0، وبالتالي هذه النقطة م، يتحرك على طول منحنى، ويقترب من النقطة بلا حدود م 0. ثم القاطع م 0 مسوف تميل إلى اتخاذ موقف مماس للمنحنى عند هذه النقطة م 0والزاوية φ→α عند Δ س→0، حيث تشير α إلى الزاوية بين المماس والاتجاه الإيجابي للمحور ثور. نظرًا لأن الدالة tan φ تعتمد بشكل مستمر على φ لـ φ≠π/2، ثم لـ φ→α tan φ → tan α، وبالتالي فإن ميل الظل سيكون:

أولئك. و "(خ)= تيراغرام α .

وهكذا هندسيا ص "(× 0)يمثل ميل المماس للرسم البياني لهذه الدالة عند هذه النقطة × 0، أي. لقيمة وسيطة معينة س، المشتق يساوي ظل الزاوية التي يشكلها مماس الرسم البياني للدالة و (خ)عند النقطة المناسبة م 0 (س؛ ص)مع اتجاه المحور الإيجابي ثور.

مثال.أوجد ميل المماس للمنحنى ص = س 2 عند النقطة م(-1; 1).

لقد سبق أن رأينا ذلك ( س 2)" = 2X. لكن المعامل الزاوي للمماس للمنحنى هو tan α = ذ"| س=-1 = – 2.

اختلاف الوظائف. استمرارية الوظيفة التفاضلية

وظيفة ص = و (س)مُسَمًّى قابل للتفاضلفي مرحلة ما س 0 إذا كان لديه مشتق معين في هذه المرحلة، أي. إذا كان حد العلاقة موجودا ومحدودا.

إذا كانت الدالة قابلة للاشتقاق عند كل نقطة في مقطع معين [ أ; ب] أو الفاصل الزمني ( أ; ب)، فيقولون أنها قابل للتفاضلعلى المقطع [ أ; ب] أو، على التوالي، في الفاصل الزمني ( أ; ب).

النظرية التالية صحيحة، حيث تحدد العلاقة بين الدوال التفاضلية والمستمرة.

نظرية.إذا كانت الوظيفة ص = و (س)قابلة للتمييز في مرحلة ما × 0، فهو مستمر عند هذه النقطة.

وهكذا، من تمايز الدالة، تتبع استمراريتها.

دليل. لو ، الذي - التي

,

حيث α هي كمية متناهية الصغر، أي. كمية تتجه إلى الصفر مثل Δ س→0. ولكن بعد ذلك

Δ ذ=F "(× 0) Δ س+αΔ س=> Δ ذ→0 عند Δ س→0، أي و(خ) - و(س 0)→0 في س→س 0 مما يعني أن الدالة و (خ)مستمر عند نقطة ما س 0 . Q.E.D.

وبالتالي، لا يمكن أن يكون للدالة مشتقة عند نقاط الانقطاع. والعكس غير صحيح: هناك دوال متصلة غير قابلة للاشتقاق في بعض النقاط (أي ليس لها مشتقة في هذه النقاط).

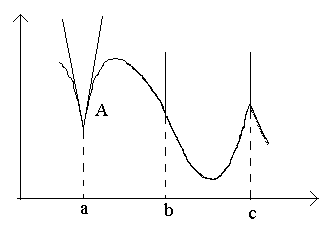
النظر في النقاط في الشكل أ، ب، ج.

عند هذه النقطة أفي Δ س→0 النسبة ليس لها حد (نظرًا لأن الحدود أحادية الجانب تختلف عن Δ س→0–0 و Δ س→0+0). عند هذه النقطة أالرسم البياني لا يوجد ظل محدد، ولكن هناك مماسين مختلفين في اتجاه واحد مع المنحدرات ل 1 و ل 2. يسمى هذا النوع من النقاط بنقطة الزاوية.

عند هذه النقطة بفي Δ سنسبة →0 هي إشارة ثابتة لكمية كبيرة بلا حدود. الدالة لها مشتق لانهائي. عند هذه النقطة، يحتوي الرسم البياني على مماس عمودي. نوع النقطة - "نقطة انعطاف" للمماس الرأسي.

عند هذه النقطة جالمشتقات أحادية الجانب هي كميات كبيرة بلا حدود من علامات مختلفة. عند هذه النقطة، يحتوي الرسم البياني على مماسين رأسيين مدمجين. النوع – “نقطة العودة” ذات المماس الرأسي – حالة خاصة لنقطة الزاوية.

توضح الأشكال أدناه أين يمكن أن تصل الدالة إلى أصغر وأكبر قيمة لها. في الشكل الأيسر، تم تثبيت القيم الأصغر والأكبر عند نقطتي الحد الأدنى والحد الأقصى المحلي للدالة. في الصورة الصحيحة - في نهايات المقطع.

إذا كانت الوظيفة ذ = F(س) مستمرة على الفترة [ أ, ب]، ثم يصل إلى هذا الجزء الأقل و أعلى القيم . وهذا، كما ذكرنا سابقًا، يمكن أن يحدث أيضًا النقاط القصوىأو في نهاية المقطع. لذلك، للعثور على الأقل و أكبر قيم الوظيفة ، مستمر على الفاصل الزمني [ أ, ب] ، تحتاج إلى حساب قيمه في الكل نقاط حرجةوفي نهايات القطعة، ثم اختر منها الأصغر والأكبر.

لنفترض، على سبيل المثال، أنك تريد تحديد أكبر قيمة للدالة F(س) على الجزء [ أ, ب] . للقيام بذلك، تحتاج إلى العثور على جميع النقاط الحرجة ملقاة على [ أ, ب] .

نقطة حرجة تسمى النقطة التي وظيفة محددة، وهي المشتقإما يساوي الصفر أو غير موجود. ثم يجب عليك حساب قيم الوظيفة عند النقاط الحرجة. وأخيرًا، يجب مقارنة قيم الدالة عند النقاط الحرجة وفي نهايات القطعة ( F(أ) و F(ب)). أكبر هذه الأرقام سيكون أكبر قيمة للدالة في المقطع [أ, ب] .

مشاكل في العثور على أصغر قيم الدالة .

نبحث عن أصغر وأكبر قيم الدالة معًا

مثال 1. ابحث عن أصغر وأكبر قيم للدالة على الجزء [-1, 2] .

حل. أوجد مشتقة هذه الدالة. دعونا نساوي المشتقة بالصفر () ونحصل على نقطتين حرجتين: و . للعثور على أصغر وأكبر قيم دالة على مقطع معين، يكفي حساب قيمها عند نهايات المقطع وعند النقطة، حيث أن النقطة لا تنتمي إلى المقطع [-1، 2]. قيم الوظائف هذه هي: , . إنه يتبع هذا أصغر قيمة دالة(المشار إليها باللون الأحمر على الرسم البياني أدناه)، والتي تساوي -7، يتم تحقيقها في الطرف الأيمن من المقطع - عند النقطة ، و أعظم(باللون الأحمر أيضًا على الرسم البياني)، يساوي 9، - عند النقطة الحرجة.

إذا كانت الدالة متصلة في فترة زمنية معينة وهذه الفترة ليست قطعة (ولكنها، على سبيل المثال، فترة؛ الفرق بين الفترة والقطعة: لا يتم تضمين النقاط الحدودية للفاصل في الفترة، ولكن يتم تضمين نقاط حدود المقطع في المقطع)، فمن بين قيم الدالة قد لا تكون الأصغر والأكبر. على سبيل المثال، الدالة الموضحة في الشكل أدناه متصلة على ]-∞، +∞[ وليس لها القيمة الأكبر.

ومع ذلك، بالنسبة لأي فترة زمنية (مغلقة أو مفتوحة أو لا نهائية)، تكون الخاصية التالية للدوال المستمرة صحيحة.

للتحقق الذاتي أثناء العمليات الحسابية، يمكنك استخدام آلة حاسبة مشتقة على الانترنت .

مثال 4. ابحث عن أصغر وأكبر قيم للدالة على الجزء [-1, 3] .

حل. نجد مشتق هذه الدالة كمشتق حاصل القسمة:

.

نحن نساوي المشتقة بالصفر، مما يعطينا نقطة حرجة واحدة: . إنه ينتمي إلى الجزء [-1، 3] . للعثور على أصغر وأكبر قيم دالة على مقطع معين، نجد قيمها في نهايات المقطع وعند النقطة الحرجة التي تم العثور عليها:

دعونا نقارن هذه القيم. الاستنتاج: يساوي -5/13 عند النقطة و أعلى قيمةيساوي 1 عند النقطة .

نواصل البحث عن القيم الأصغر والأكبر للدالة معًا

هناك مدرسون، فيما يتعلق بموضوع إيجاد أصغر وأكبر قيم للدالة، لا يعطوا الطلاب أمثلة لحلها تكون أكثر تعقيدًا من تلك التي تمت مناقشتها للتو، أي تلك التي تكون فيها الدالة كثيرة الحدود أو دالة الكسر الذي بسطه ومقامه كثيرات الحدود. لكننا لن نقتصر على مثل هذه الأمثلة، لأنه من بين المعلمين هناك من يحب إجبار الطلاب على التفكير بالكامل (جدول المشتقات). ولذلك، سيتم استخدام الدالة اللوغاريتمية والدالة المثلثية.

مثال 8. ابحث عن أصغر وأكبر قيم للدالة على الجزء .

حل. نجد مشتقة هذه الوظيفة كما مشتق من المنتج :

نحن نساوي المشتقة بالصفر، وهو ما يعطي نقطة حرجة واحدة: . إنه ينتمي إلى هذا الجزء. للعثور على أصغر وأكبر قيم دالة على مقطع معين، نجد قيمها في نهايات المقطع وعند النقطة الحرجة التي تم العثور عليها:

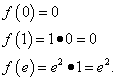
نتيجة جميع الإجراءات: تصل الدالة إلى الحد الأدنى من قيمتها، يساوي 0، عند النقطة وعند النقطة و أعلى قيمة، متساوي ه²، عند هذه النقطة.

للتحقق الذاتي أثناء العمليات الحسابية، يمكنك استخدام آلة حاسبة مشتقة على الانترنت .

مثال 9. ابحث عن أصغر وأكبر قيم للدالة على الجزء .

حل. أوجد مشتقة هذه الدالة:

نحن نساوي المشتقة بالصفر:

النقطة الحرجة الوحيدة تنتمي إلى هذا القطاع. للعثور على أصغر وأكبر قيم دالة على مقطع معين، نجد قيمها في نهايات المقطع وعند النقطة الحرجة التي تم العثور عليها:

خاتمة: تصل الدالة إلى الحد الأدنى من قيمتها، يساوي ، عند النقطة و أعلى قيمة, على قدم المساواة , عند هذه النقطة .

في المسائل المتطرفة المطبقة، عادةً ما يكون العثور على القيم الأصغر (القصوى) للدالة بمثابة إيجاد الحد الأدنى (الحد الأقصى). ولكن ليس الحد الأدنى أو الحد الأقصى في حد ذاته هو الذي له أهمية عملية أكبر، ولكن قيم الحجة التي يتم تحقيقها من خلالها. عند حل المهام التطبيقية، تنشأ صعوبة إضافية - تكوين وظائف تصف الظاهرة أو العملية قيد النظر.

مثال 10.يجب أن يكون الخزان بسعة 4، على شكل متوازي السطوح وقاعدة مربعة ومفتوح من الأعلى، معلبًا. ما هو الحجم الذي يجب أن يكون عليه الخزان بحيث يتم استخدام أقل كمية من المواد لتغطيته؟

حل. يترك س- الجانب الأساسي، ح- ارتفاع الخزان، س- مساحة سطحه بدون غطاء، الخامس- حجمه. يتم التعبير عن مساحة سطح الخزان بالصيغة، أي. هي دالة لمتغيرين. للتعبير سكدالة لمتغير واحد، نستخدم حقيقة أنه من أين . استبدال التعبير الموجود حفي الصيغة ل س:

دعونا نفحص هذه الوظيفة إلى أقصى الحدود. يتم تعريفه وتمييزه في كل مكان في ]0 و +∞[ و

.

نحن نساوي المشتقة بالصفر () ونجد النقطة الحرجة. بالإضافة إلى ذلك، عندما لا يكون المشتق موجودًا، ولكن هذه القيمة لا تدخل في مجال التعريف وبالتالي لا يمكن أن تكون نقطة متطرفة. لذلك، هذه هي النقطة الحرجة الوحيدة. دعونا نتحقق من وجود الحد الأقصى باستخدام علامة الكافية الثانية. دعونا نجد المشتق الثاني. عندما يكون المشتق الثاني أكبر من الصفر (). وهذا يعني أنه عندما تصل الدالة إلى الحد الأدنى . منذ هذا الحد الأدنى هو الحد الأقصى الوحيد لهذه الدالة، وهو أصغر قيمة لها. لذلك يجب أن يكون طول ضلع قاعدة الخزان 2 متر وارتفاعه .

للتحقق الذاتي أثناء العمليات الحسابية، يمكنك استخدام

من الناحية العملية، الفائدة الأكبر هي استخدام المشتق للعثور على أكبر وأصغر قيم للدالة. ما علاقة هذا؟ تعظيم الأرباح وتقليل التكاليف وتحديد الحمل الأمثل للمعدات... بمعنى آخر، يتعين علينا في العديد من مجالات الحياة حل مشكلات تحسين بعض المعلمات. وهذه هي مهام إيجاد القيم الأكبر والأصغر للدالة.

تجدر الإشارة إلى أنه عادة ما يتم البحث عن القيم الأكبر والأصغر للدالة في فترة معينة X، وهي إما مجال الدالة بالكامل أو جزء من مجال التعريف. الفاصل الزمني X نفسه يمكن أن يكون قطعة، فاصل زمني مفتوح ، فاصل لا نهائي.

سنتحدث في هذه المقالة عن إيجاد أكبر وأصغر قيم لدالة محددة بوضوح لمتغير واحد y=f(x) .

التنقل في الصفحة.

أكبر وأصغر قيمة للدالة - التعريفات والرسوم التوضيحية.

دعونا نلقي نظرة سريعة على التعاريف الرئيسية.

أكبر قيمة للدالة ذلك لأي شخص عدم المساواة صحيح.

أصغر قيمة للدالة y=f(x) على الفاصل الزمني X تسمى هذه القيمة ذلك لأي شخص عدم المساواة صحيح.

هذه التعريفات بديهية: القيمة الأكبر (الأصغر) للدالة هي أكبر (أصغر) قيمة مقبولة في الفترة قيد النظر عند الإحداثي السيني.

نقاط ثابتة– هذه هي قيم الوسيطة التي يصبح عندها مشتق الدالة صفراً.

لماذا نحتاج إلى نقاط ثابتة عند إيجاد القيم الأكبر والأصغر؟ الجواب على هذا السؤال يأتي من نظرية فيرما. ويترتب على هذه النظرية أنه إذا كانت الدالة القابلة للتفاضل لها حد أقصى (حد أدنى محلي أو حد أقصى محلي) في مرحلة ما، فإن هذه النقطة تكون ثابتة. وبالتالي، فإن الدالة غالبًا ما تأخذ أكبر (أصغر) قيمة لها على الفاصل الزمني X عند إحدى النقاط الثابتة من هذا الفاصل الزمني.

كما أن الدالة يمكن أن تأخذ قيمها الأكبر والأصغر في كثير من الأحيان عند نقاط لا يوجد فيها المشتق الأول لهذه الدالة، ويتم تعريف الدالة نفسها.

دعنا نجيب على الفور على أحد الأسئلة الأكثر شيوعًا حول هذا الموضوع: "هل من الممكن دائمًا تحديد القيمة الأكبر (الأصغر) للدالة"؟ لا، ليس دائما. في بعض الأحيان تتطابق حدود الفاصل الزمني X مع حدود مجال تعريف الدالة، أو يكون الفاصل الزمني X لانهائيًا. وبعض الدوال عند اللانهاية وعند حدود مجال التعريف يمكن أن تأخذ قيمًا كبيرة بلا حدود وقيمًا صغيرة بلا حدود. في هذه الحالات، لا يمكن قول أي شيء عن القيمة الأكبر والأصغر للدالة.

من أجل الوضوح، سنقدم رسما توضيحيا. انظر إلى الصور وسيصبح الكثير أكثر وضوحًا.

على الجزء

في الشكل الأول، تأخذ الدالة القيم الأكبر (max y) والأصغر (min y) عند نقاط ثابتة تقع داخل المقطع [-6;6].

النظر في الحالة المبينة في الشكل الثاني. دعونا نغير المقطع إلى . في هذا المثال، يتم تحقيق أصغر قيمة للدالة عند نقطة ثابتة، والقيمة الأكبر عند النقطة التي يتوافق فيها الإحداثي الإحداثي مع الحد الأيمن للفاصل الزمني.

في الشكل 3، النقاط الحدودية للمقطع [-3;2] هي حدود النقاط المقابلة لأكبر وأصغر قيمة للدالة.

على فترة مفتوحة

في الشكل الرابع، تأخذ الدالة القيم الأكبر (max y) والأصغر (min y) عند نقاط ثابتة تقع داخل الفترة المفتوحة (-6;6).

في الفترة، لا يمكن استخلاص أي استنتاجات حول القيمة الأكبر.

في اللانهاية

في المثال المعروض في الشكل السابع، تأخذ الدالة القيمة الأكبر (max y) عند نقطة ثابتة مع الإحداثي السيني x=1، ويتم تحقيق أصغر قيمة (min y) على الحد الأيمن للفاصل الزمني. عند علامة ناقص اللانهاية، تقترب قيم الدالة بشكل مقارب من y=3.

خلال الفترة، لا تصل الدالة إلى القيمة الأصغر أو الأكبر. عندما تقترب x=2 من اليمين، تميل قيم الدالة إلى سالب ما لا نهاية (الخط x=2 هو خط مقارب عمودي)، وبما أن الإحداثي السيني يميل إلى زائد اللانهاية، فإن قيم الدالة تقترب بشكل غير مقارب من y=3. يظهر الرسم التوضيحي لهذا المثال في الشكل 8.

خوارزمية للعثور على أكبر وأصغر قيم للدالة المستمرة على القطعة.

دعونا نكتب خوارزمية تسمح لنا بالعثور على أكبر وأصغر قيم للدالة على القطعة.

1. نجد مجال تعريف الوظيفة ونتحقق مما إذا كانت تحتوي على المقطع بأكمله.
2. نجد جميع النقاط التي لا يوجد عندها المشتق الأول والموجودة في المقطع (عادةً ما توجد هذه النقاط في الوظائف ذات الوسيطة تحت علامة المعامل وفي وظائف القوة ذات الأس الكسرى). إذا لم تكن هناك مثل هذه النقاط، فانتقل إلى النقطة التالية.
3. نحدد جميع النقاط الثابتة التي تقع ضمن المقطع. للقيام بذلك، نساويه بالصفر، ونحل المعادلة الناتجة ونختار الجذور المناسبة. إذا لم تكن هناك نقاط ثابتة أو لم يقع أي منها في المقطع، فانتقل إلى النقطة التالية.
4. نحسب قيم الدالة عند نقاط ثابتة محددة (إن وجدت)، عند النقاط التي لا يوجد عندها المشتق الأول (إن وجد)، وكذلك عند x=a وx=b.
5. من قيم الوظيفة التي تم الحصول عليها، نختار الأكبر والأصغر - ستكون القيم الأكبر والأصغر المطلوبة للوظيفة، على التوالي.

دعونا نحلل الخوارزمية لحل مثال للعثور على أكبر وأصغر قيم للدالة على القطعة.

مثال.

أوجد أكبر وأصغر قيمة للدالة

• على المقطع؛
• على المقطع [-4;-1] .

حل.

مجال تعريف الدالة هو مجموعة الأعداد الحقيقية بأكملها، باستثناء الصفر. كلا القطاعين يقعان ضمن مجال التعريف.

أوجد مشتقة الدالة بالنسبة إلى:

من الواضح أن مشتق الدالة موجود في جميع نقاط القطع و [-4;-1].

نحدد النقاط الثابتة من المعادلة. الجذر الحقيقي الوحيد هو x=2 تقع هذه النقطة الثابتة في الجزء الأول.

في الحالة الأولى، نحسب قيم الدالة عند نهايات المقطع وعند النقطة الثابتة، أي بالنسبة لـ x=1 وx=2 وx=4:

وبالتالي فإن القيمة الأكبر للدالة يتم تحقيقه عند x=1، وأصغر قيمة – عند س=2.

في الحالة الثانية، نحسب قيم الدالة فقط في نهايات المقطع [-4;-1] (نظرًا لأنه لا يحتوي على نقطة ثابتة واحدة):

حل.

لنبدأ بمجال الوظيفة. يجب ألا تختفي ثلاثية الحدود المربعة في مقام الكسر:

من السهل التحقق من أن جميع الفواصل الزمنية من بيان المشكلة تنتمي إلى مجال تعريف الوظيفة.

دعونا نفرق الوظيفة:

من الواضح أن المشتق موجود في كامل مجال تعريف الدالة.

دعونا نجد النقاط الثابتة. المشتق يذهب إلى الصفر عند . تقع هذه النقطة الثابتة ضمن الفترتين (-3;1] و(-3;2).

يمكنك الآن مقارنة النتائج التي تم الحصول عليها عند كل نقطة بالرسم البياني للدالة. الخطوط المنقطة الزرقاء تشير إلى الخطوط المقاربة.

عند هذه النقطة يمكننا الانتهاء من إيجاد القيم الأكبر والأصغر للدالة. تتيح لك الخوارزميات التي تمت مناقشتها في هذه المقالة الحصول على نتائج بأقل عدد من الإجراءات. ومع ذلك، قد يكون من المفيد أولاً تحديد فترات الزيادة والنقصان للدالة وفقط بعد ذلك استخلاص استنتاجات حول أكبر وأصغر قيم للدالة في أي فاصل زمني. وهذا يعطي صورة أوضح وتبريرًا صارمًا للنتائج.

تعريف3 . 3 دع بعض الوظائف ومجال تعريفها وبعض الفاصل الزمني (المفتوح) (ربما مع و/أو ) 7 . لنستدعي الدالة مستمر على الفاصل الزمني، إذا كان مستمرا في أي نقطة، وهذا هو، لأي هناك (بصيغة مختصرة:

لنكن الآن جزءًا (مغلقًا) في . لنستدعي الدالة المستمر على الجزء، إذا كانت مستمرة على الفترة، ومستمرة على اليمين عند النقطة، ومستمرة على اليسار عند النقطة، أي

مثال3 . 13 النظر في الوظيفة (وظيفة هيفيسايد) على الجزء . ثم تكون متصلة على القطعة (على الرغم من أنها عند هذه النقطة بها انقطاع من النوع الأول).

الشكل 3.15 رسم بياني لدالة هيفيسايد

يمكن إعطاء تعريف مماثل لفترات نصفية من النموذج و، بما في ذلك الحالات و. ومع ذلك، يمكننا تعميم هذا التعريف على حالة مجموعة فرعية عشوائية على النحو التالي. دعونا أولا نقدم هذا المفهوم الناجم عنإلى القواعد: دع القاعدة التي تحتوي جميع نهاياتها على تقاطعات غير فارغة مع . دعونا نشير بواسطة وننظر في مجموعة الكل. ومن ثم فمن السهل التحقق من أن المجموعة سوف تكون القاعدة. وبالتالي، بالنسبة للقواعد، و، وأين، و هي قواعد الأحياء غير المثقوبة ذات الوجهين (يسار، يمين، على التوالي) لنقطة ما (انظر تعريفها في بداية الفصل الحالي).

تعريف3 . 4 لنستدعي الدالة مستمر على المجموعة، لو

من السهل أن نرى أن عند هذا التعريف وفيه يتزامن مع التعريفات المذكورة أعلاه خصيصًا للفاصل الزمني والمقطع.

تذكر أن جميع الدوال الأولية تكون متصلة في جميع نقاط نطاق تعريفها، وبالتالي فهي متصلة على أي فترات أو قطع تقع في نطاق تعريفها.

نظرًا لأن الاستمرارية على الفاصل الزمني والمقطع محددة بشكل نقطي، فإن النظرية تظل صحيحة، وهي نتيجة مباشرة للنظرية 3.1:

نظرية3 . 5 يترك و - وظائف و - الفاصل الزمني أو الجزء الموجود . يترك و مستمر ل . ثم الوظائف , , مستمر ل . إذا بالإضافة إلى ذلك أمام الجميع ، ثم الدالة مستمر أيضًا .

يتبع البيان التالي من هذه النظرية، تمامًا كما هو الحال في النظرية 3.1 - الاقتراح 3.3:

يعرض3 . 4 مجموعة من جميع الوظائف مستمرة على فترة أو قطعة - هذه مساحة خطية:

يتم التعبير عن خاصية أكثر تعقيدًا للدالة المستمرة من خلال النظرية التالية.

نظرية3 . 6 (حول جذر الدالة المستمرة) دع الوظيفة المستمر على الجزء ، و و - أعداد من العلامات المختلفة. (من أجل اليقين، سنفترض ذلك ، أ .) ثم هناك قيمة واحدة على الأقل من هذا القبيل ، ماذا (أي أن هناك جذرًا واحدًا على الأقل المعادلات ).

دليل. دعونا ننظر إلى منتصف الجزء. ثم إما أن يكون، أو، أو. في الحالة الأولى، تم العثور على الجذر: هذا هو . في الحالتين المتبقيتين، ضع في اعتبارك ذلك الجزء من المقطع الذي تأخذ الدالة في نهايته قيم علامات مختلفة: في حالة أو في حالة . نشير إلى النصف المحدد من المقطع ونطبق عليه نفس الإجراء: نقسمه إلى نصفين و أين و نجد . في حالة العثور على الجذر؛ في حالة النظر في هذا الجزء بشكل أكبر في حالة - الجزء إلخ.

الشكل 3.16 التقسيمات المتتالية للقطعة إلى النصف

لقد حصلنا على أنه إما في خطوة ما سيتم العثور على الجذر، أو سيتم إنشاء نظام من الأجزاء المتداخلة

حيث يكون كل جزء لاحق نصف طول الجزء السابق. التسلسل غير تنازلي ومحدود من الأعلى (على سبيل المثال، بالرقم)؛ ولذلك (بحسب النظرية 2.13)، فإن لها نهاية. التبعية - غير متزايد ومحدود من الأسفل (على سبيل المثال، بالرقم)؛ هذا يعني أن هناك حدًا. نظرًا لأن أطوال المقاطع تشكل تقدمًا هندسيًا متناقصًا (مع المقام)، فإنها تميل إلى 0، و ، إنه . دعونا نضعها الآن. ثم

و

بما أن الدالة مستمرة . ومع ذلك، من خلال بناء التسلسلات و و، بحيث، من خلال نظرية المرور إلى الحد في عدم المساواة (نظرية 2.7)، و هذا هو و . هذا يعني أن و هو جذر المعادلة.

مثال3 . 14 النظر في الوظيفة على الجزء. وبما أن و هي أرقام ذات علامات مختلفة، فإن الدالة تتحول إلى 0 في مرحلة ما في الفترة. وهذا يعني أن المعادلة لها جذر.

الشكل 3.17: تمثيل رسومي لجذر المعادلة

تعطينا النظرية المثبتة طريقة للعثور على الجذر، على الأقل بشكل تقريبي، بأي درجة من الدقة محددة مسبقًا. هذه هي طريقة تقسيم القطعة إلى النصف، الموضحة في إثبات النظرية. سنتعرف على هذه وغيرها من الطرق الأكثر فعالية للعثور على الجذر تقريبًا بمزيد من التفاصيل أدناه، بعد أن ندرس مفهوم وخصائص المشتق.

لاحظ أن النظرية لا تنص على أنه إذا تم استيفاء شروطها، فإن الجذر يكون فريدًا. كما يوضح الشكل التالي، يمكن أن يكون هناك أكثر من جذر واحد (يوجد 3 في الشكل).

الشكل 3.18 عدة جذور لدالة تأخذ قيم إشارات مختلفة في نهايات المقطع

ومع ذلك، إذا زادت الدالة بشكل رتيب أو انخفضت بشكل رتيب على مقطع ما، وفي نهايتها تأخذ قيم علامات مختلفة، فإن الجذر يكون فريدًا، نظرًا لأن الدالة الرتيبة بدقة تأخذ كل قيمة من قيمها عند نقطة واحدة بالضبط بما في ذلك القيمة 0.

الشكل 3.19: لا يمكن أن يكون للدالة الرتيبة أكثر من جذر واحد

النتيجة المباشرة للنظرية على جذر دالة مستمرة هي النظرية التالية، والتي في حد ذاتها مهمة جدًا في التحليل الرياضي.

نظرية3 . 7 (حول القيمة المتوسطة للدالة المستمرة) دع الوظيفة المستمر على الجزء و (من أجل اليقين سنفترض ذلك ). يترك - بعض الأرقام تقع بين و . ثم هناك مثل هذه النقطة ، ماذا .

الشكل 3.20: تأخذ الوظيفة المستمرة أي قيمة متوسطة

دليل. النظر في وظيفة المساعد ، أين . ثم و . من الواضح أن الدالة مستمرة، وحسب النظرية السابقة هناك نقطة مثل . لكن هذه المساواة تعني ذلك.

لاحظ أنه إذا كانت الدالة غير متصلة، فقد لا تأخذ جميع القيم المتوسطة. على سبيل المثال، تأخذ دالة Heaviside (انظر المثال 3.13) القيم، ولكن لا تأخذ، على سبيل المثال، قيمة متوسطة في أي مكان، بما في ذلك الفاصل الزمني. الحقيقة هي أن دالة هيفيسايد لها انقطاع عند نقطة تقع بالضبط في الفترة.

لمزيد من الدراسة لخصائص الدوال المستمرة على فترة ما، سنحتاج إلى الخاصية الدقيقة التالية لنظام الأعداد الحقيقية (لقد ذكرناها بالفعل في الفصل الثاني فيما يتعلق بنظرية نهاية دالة محدودة رتابة متزايدة): أي مجموعة يحدها أدناه (أي، بحيث يتم استدعاء الرقم للجميع وبعضهم الحافة السفليةمجموعات) المتاحة الحافة السفلية بالضبطأي أن العدد الأكبر من ذلك ينطبق على الجميع. وبالمثل، إذا كانت المجموعة محدودة من الأعلى، فهي كذلك الحد الأعلى الدقيق: وهذا هو أصغر من أعلى الوجوه(من أجل الجميع).

الشكل 3.21: الحدود الدنيا والعليا لمجموعة محددة

إذا كان هناك تسلسل غير متزايد من النقاط التي تميل إلى . وبنفس الطريقة، إذا كان هناك تسلسل غير متناقص من النقاط التي تميل إلى .

إذا كانت هناك نقطة تنتمي إلى المجموعة، فهي أصغر عنصر في هذه المجموعة: ; بالمثل إذا ، الذي - التي .

وبالإضافة إلى ذلك، لمزيد من سنحتاج إلى ما يلي

ليما3 . 1 يترك - دالة مستمرة على القطعة ، والعديد تلك النقاط ، بحيث (أو ، أو ) ليس فارغا. ثم بكثرة هناك أصغر قيمة ، مثل ذلك أمام الجميع .

الشكل 3.22 أصغر وسيطة تأخذ فيها الدالة القيمة المحددة

دليل. نظرًا لأنها مجموعة محدودة (وهي جزء من قطعة)، فهي تحتوي على الحد الأدنى. ثم يوجد تسلسل غير متزايد، مثل . وعلاوة على ذلك، من خلال تعريف مجموعة. ولذلك، وبالانتقال إلى الحد الأقصى، نحصل، من ناحية، على:

ومن ناحية أخرى، ونظرًا لاستمرارية الوظيفة،

وهذا يعني أن النقطة تنتمي إلى المجموعة و .

في الحالة التي يتم فيها تعريف المجموعة بالمتباينة، لدينا للجميع وبنظرية المرور إلى الحد في المتباينة التي نحصل عليها

من أين، وهو ما يعني أن و. وبالمثل، في حالة المتباينة، فإن المرور إلى الحد في المتباينة يعطي

من أين و.

نظرية3 . 8 (حول حدود دالة مستمرة) دع الوظيفة المستمر على الجزء . ثم تقتصر على أي أن هناك مثل هذا الثابت ، ماذا أمام الجميع .

الشكل 3.23: دالة متصلة على مقطع محدد

دليل. لنفترض العكس: فلا يقتصر الأمر، على سبيل المثال، من فوق. إذن جميع المجموعات , , ليست فارغة. حسب الليما السابقة، كل مجموعة من هذه المجموعات لها أصغر قيمة، . دعونا نظهر ذلك

حقًا، . إذا كانت أي نقطة من ، على سبيل المثال، تقع بين و، إذن

أي قيمة متوسطة بين و . هذا يعني أنه وفقًا للنظرية المتعلقة بالقيمة الوسيطة للدالة المستمرة، توجد نقطة من هذا القبيل ، و . ولكن، خلافا للافتراض القائل بأن - أصغر قيمة للمجموعة. ويترتب على ذلك للجميع.

وبنفس الطريقة، تم إثبات ذلك أيضًا للجميع، للجميع، وما إلى ذلك. لذلك، هناك تسلسل متزايد يحده الرقم أعلاه. ولذلك فهو موجود. من استمرارية الوظيفة يترتب على ذلك أن هناك ، لكن في، لذلك ليس هناك حد. يثبت التناقض الناتج أن الدالة محدودة بالأعلى.

وثبت بطريقة مماثلة أنها محدودة من الأسفل، مما يعني ضمنا بيان النظرية.

من الواضح أنه من المستحيل إضعاف شروط النظرية: إذا كانت الدالة غير متصلة، فلا يلزم أن تكون محدودة بفاصل زمني (نعطي الدالة كمثال

على الجزء. هذه الدالة غير محدودة بالفاصل الزمني، حيث أن عند لديها نقطة انقطاع من النوع الثاني، مثل ذلك في . من المستحيل أيضًا استبدال قطعة في حالة النظرية بفاصل زمني أو نصف فاصل: على سبيل المثال، فكر في نفس الوظيفة على نصف فاصل زمني. تكون الدالة مستمرة في نصف الفترة هذه، ولكنها غير محدودة، نظرًا لحقيقة أنه عند .

إن العثور على أفضل الثوابت التي يمكن استخدامها لتحديد دالة من الأعلى والأسفل خلال فترة زمنية معينة يقودنا بطبيعة الحال إلى مشكلة إيجاد الحد الأدنى والحد الأقصى للدالة المستمرة في هذه الفترة. يتم وصف إمكانية حل هذه المشكلة من خلال النظرية التالية.

نظرية3 . 9 (حول الوصول إلى الحد الأقصى بواسطة وظيفة مستمرة) دع الوظيفة المستمر على الجزء . ثم هناك نقطة ، مثل ذلك أمام الجميع (إنه - الحد الأدنى للنقطة: )، وهناك نقطة ، مثل ذلك أمام الجميع (إنه - النقطة القصوى: ). وبعبارة أخرى، الحد الأدنى والحد الأقصى 8 توجد قيم دالة مستمرة على مقطع ما ويتم تحقيقها في بعض النقاط و هذا الجزء.

الشكل 3.24: الدالة المستمرة على مقطع تصل إلى الحد الأقصى والأدنى

دليل. بما أنه وفقًا للنظرية السابقة، فإن الدالة يحدها ما فوق، إذن هناك حد أعلى دقيق لقيم الدالة بواسطة - الرقم . وبالتالي فإن المجموعات، ,..., ,..., ليست فارغة، وحسب الليما السابقة فإنها تحتوي على أصغر القيم: ، . هذه لا تنقص (تم إثبات هذه العبارة بنفس الطريقة تمامًا كما في النظرية السابقة):

وتقتصر من فوق بواسطة . لذلك، وفقًا لنظرية نهاية التسلسل الرتيب المحدود، هناك حد منذ ذلك الحين ، ثم

بواسطة نظرية المرور إلى نهاية المتباينة، أي . ولكن مع الجميع، بما في ذلك. ومن هذا يتبين أن الحد الأقصى للدالة يتحقق عند النقطة.

تم إثبات وجود نقطة دنيا بطريقة مماثلة.

في هذه النظرية، كما في النظرية السابقة، من المستحيل إضعاف الشروط: إذا كانت الدالة غير متصلة، فقد لا تصل إلى قيمتها القصوى أو الدنيا على القطعة، حتى لو كانت محدودة. على سبيل المثال، لنأخذ الوظيفة

على الجزء. هذه الوظيفة محدودة بالفاصل الزمني (من الواضح) و ومع ذلك، فإنه لا يأخذ القيمة 1 عند أي نقطة من المقطع (لاحظ ذلك، وليس 1). والحقيقة هي أن هذه الدالة لها انقطاع من النوع الأول عند النقطة، بحيث لا تساوي عند النهاية قيمة الدالة عند النقطة 0. علاوة على ذلك، فإن الدالة المستمرة المعرفة على فترة أو مجموعة أخرى ليست كذلك يمكن أيضًا للجزء المغلق (على نصف الفاصل الزمني ونصف المحور) ألا يأخذ قيمًا متطرفة. على سبيل المثال، النظر في وظيفة على الفاصل الزمني. من الواضح أن الدالة مستمرة وأن الدالة لا تأخذ القيمة 0 ولا القيمة 1 عند أي نقطة في الفترة. دعونا نفكر أيضًا في الوظيفة على رمح المحور. هذه الدالة مستمرة على ، وتزداد، وتأخذ قيمتها الدنيا 0 عند النقطة، ولكنها لا تأخذ قيمة قصوى عند أي نقطة (على الرغم من أنها محدودة من الأعلى بالرقم و

تعريف. إذا كانت الوظيفة F(س) يتم تعريفه على الفاصل الزمني [ أ، ب]، مستمرة عند كل نقطة من الفترة ( أ، ب)، عند نقطة أمستمرة على اليمين، عند هذه النقطة بمستمرة على اليسار، فنقول أن الدالة F(س) المستمر على الجزء [أ، ب].

وبعبارة أخرى، الوظيفة F(س) مستمرة على الفترة [ أ، ب] إذا توفرت ثلاثة شروط:

1) "س 0 Î( أ، ب): F(س) = F(س 0);

2) F(س) = F(أ);

3) F(س) = F(ب).

بالنسبة للدوال المتصلة على فترة ما، فإننا نأخذ في الاعتبار بعض الخصائص، والتي نصيغها في شكل النظريات التالية، دون إجراء البراهين.

النظرية 1. إذا كانت الوظيفة F(س) مستمرة على الفترة [ أ، ب]، ثم يصل إلى الحد الأدنى والحد الأقصى لقيمه على هذا الجزء.

تنص هذه النظرية (الشكل 1.15) على أنه في المقطع [ أ، ب] هناك مثل هذه النقطة س 1 ذلك F(س 1) جنيه استرليني F(س) لأي سمن [ أ، ب] وأن هناك نقطة س 2 (س 2 أو[ أ، ب]) مثل ذلك " سÎ[ أ، ب] (F(س 2)³ F(س)).

معنى F(س 1) هو الأكبر لوظيفة معينة على [ أ، ب]، أ F(س 2) – الأصغر . دعنا نشير إلى: F(س 1) = م, F(س 2) =م. منذ ل F(س) عدم المساواة يحمل: " سÎ[ أ، ب] م£ F(س) £ م، ثم نحصل على النتيجة الطبيعية التالية من النظرية 1.

عاقبة. إذا كانت الوظيفة F(س) متصلة على فترة، فهي محصورة في هذه الفترة.

النظرية 2. إذا كانت الوظيفة F(س) مستمرة على الفترة [ أ، ب] وفي نهايات المقطع يأخذ قيم علامات مختلفة، ثم هناك مثل هذه النقطة الداخلية س 0 شريحة [ أ، ب]، حيث تتحول الدالة إلى 0، أي. $ س 0 Î ( أ، ب) (F(س 0) = 0).

تنص هذه النظرية على أن الرسم البياني للدالة ص = و(س) ، مستمر على الفاصل الزمني [ أ، ب]، يتقاطع مع المحور ثورمرة واحدة على الأقل إذا كانت القيم F(أ) و F(ب) لها علامات معاكسة. لذلك، (الشكل 1.16) F(أ) > 0, F(ب) < 0 и функция F(س) يصبح 0 عند النقاط س 1 , س 2 , س 3 .

النظرية 3. دع الوظيفة F(س) مستمرة على الفترة [ أ، ب], F(أ) = أ, F(ب) = بو أ¹ ب. (الشكل 1.17). ثم لأي رقم ج، محصور بين الأرقام أو ب، هناك مثل هذه النقطة الداخلية س 0 شريحة [ أ، ب]، ماذا F(س 0) = ج.

عاقبة. إذا كانت الوظيفة F(س) مستمرة على الفترة [ أ، ب], م- أصغر قيمة F(س), م- أكبر قيمة للدالة F(س) على الجزء [ أ، ب]، فإن الدالة تأخذ (مرة واحدة على الأقل) أي قيمة م، خلص بين مو م، وبالتالي الجزء [ مم] هي مجموعة جميع قيم الوظائف F(س) على الجزء [ أ، ب].

لاحظ أنه إذا كانت الدالة متصلة على الفترة ( أ، ب) أو لديه على الجزء [ أ، ب] نقاط الانقطاع، فإن النظريات 1، 2، 3 لمثل هذه الوظيفة تتوقف عن أن تكون صحيحة.

في الختام، النظر في نظرية وجود دالة عكسية.

النظرية 4. يترك F(س) مستمرة على الفترة X، يزيد (أو ينقص) بمقدار Xولها مجموعة من القيم ي. ثم للوظيفة ص = و(س) هناك وظيفة عكسية س= ي(ذ) ، محددة على الفاصل الزمني ي، مستمرة ومتزايدة (أو متناقصة) بواسطة يمع معاني متعددة X.

تعليق. دع الوظيفة س= ي(ذ) هو معكوس الدالة F(س). بما أن الحجة يُشار إليها عادةً بـ س، والدالة من خلال ذثم نكتب الدالة العكسية على الصورة ص =ي(س).

مثال 1. وظيفة ص = س 2 (الشكل 1.8، أ) على المجموعة X= }