Спектр двух прямоугольных импульсов. Спектральный состав последовательности прямоугольных импульсов при различном периоде их скважности
Литература: [Л.1], с 40
В качестве примера приведем разложение в ряд Фурье периодической последовательности прямоугольных импульсов с амплитудой , длительностью и периодом следования , симметричной относительно нуля, т.е.
 , (2.10)
, (2.10)
Здесь 
Разложение такого сигнала в ряд Фурье дает
 , (2.11)
, (2.11)
где – скважность.
Для упрощения записи можно ввести обозначение
 , (2.12)
, (2.12)
Тогда (2.11) запишется следующим образом
 , (2.13)
, (2.13)
На рис. 2.3 изображена последовательность прямоугольных импульсов. Спектр последовательности, как впрочем, и любого другого периодического сигнала, носит дискретный (линейчатый) характер.
Огибающая спектра (рис. 2.3, б) пропорциональна  . Расстояние по оси частот между двумя соседними составляющими спектра равно , а между двумя нулевыми значениями (ширина лепестка спектра) – . Число гармонических составляющих в пределах одного лепестка, включая правое по рисунку нулевое значение, составляет , где знак означает округление до ближайшего целого числа, меньшего (если скважность – дробное число), или (при целочисленном значении скважности). При увеличении периода основная частота
. Расстояние по оси частот между двумя соседними составляющими спектра равно , а между двумя нулевыми значениями (ширина лепестка спектра) – . Число гармонических составляющих в пределах одного лепестка, включая правое по рисунку нулевое значение, составляет , где знак означает округление до ближайшего целого числа, меньшего (если скважность – дробное число), или (при целочисленном значении скважности). При увеличении периода основная частота  уменьшается, спектральные составляющие на диаграмме сближаются, амплитуды гармоник также уменьшаются. При этом форма огибающей сохраняется.
уменьшается, спектральные составляющие на диаграмме сближаются, амплитуды гармоник также уменьшаются. При этом форма огибающей сохраняется.




При решении практических задач спектрального анализа вместо угловых частот используют циклические частоты  , измеряемые в Герцах. Очевидно, расстояние между соседними гармониками на диаграмме составит , а ширина одного лепестка спектра – . Эти значения представлены на диаграмме в круглых скобках.
, измеряемые в Герцах. Очевидно, расстояние между соседними гармониками на диаграмме составит , а ширина одного лепестка спектра – . Эти значения представлены на диаграмме в круглых скобках.
В практической радиотехнике в большинстве случаев вместо спектрального представления (рис. 2.3, б) используют спектральные диаграммы амплитудного и фазового спектров. Амплитудный спектр последовательности прямоугольных импульсов представлен на рис. 2.3, в.
Очевидно, огибающая амплитудного спектра пропорциональна  .
.
Что же касается фазового спектра (рис. 2.3, г), то полагают, что начальные фазы гармонических составляющих изменяются скачком на величину -π при изменение знака огибающей sinc kπ/q . Начальные фазы гармоник первого лепестка, полагаются равными нулю. Тогда начальные фазы гармоник второго лепестка составят φ = -π , третьего лепестка φ = -2π и т.д.
Рассмотрим еще одно представление сигнала рядом Фурье. Для этого воспользуемся формулой Эйлера
 .
.
В соответствии с этой формулой k-ю составляющую (2.9) разложения сигнала в ряд Фурье можно представить следующим образом
 ;
;  . (2.15)
. (2.15)
Здесь величины и являются комплексными и представляют собой комплексные амплитуды составляющих спектра. Тогда ряд
Фурье (2.8) с учетом (2.14) примет следующую форму
 , (2.16)
, (2.16)
 , (2.17)
, (2.17)
Нетрудно убедиться в том, что разложение (2.16) проводится по базисным функциям  , которые также являются ортогональными на интервале
, которые также являются ортогональными на интервале  , т.е.
, т.е.

Выражение (2.16) представляет собой комплексную форму
ряда Фурье, которая распространяется на отрицательные частоты. Величины и  , где означает комплексную сопряженную с величину, называются комплексными амплитудами
спектра. Т.к. является комплексной величиной, из (2.15) следует, что
, где означает комплексную сопряженную с величину, называются комплексными амплитудами
спектра. Т.к. является комплексной величиной, из (2.15) следует, что
 и
и  .
.
Тогда совокупность составляет амплитудный, а совокупность – фазовый спектр сигнала .

На рис. 2.4 представлена спектральная диаграмма спектра рассмотренной выше последовательности прямоугольных импульсов, представленного комплексным рядом Фурье

Спектр также носит линейчатый характер, но в отличие от ранее рассмотренных спектров определяется как в области положительных, так и в области отрицательных частот. Поскольку является чётной функцией аргумента , спектральная диаграмма симметрична относительно нуля.
Исходя из (2.15) можно установить соответствие между и коэффициентами и разложения (2.3). Так как
 и
и  ,
,
то в результате получим
 . (2.18)
. (2.18)
Выражения (2.5) и (2.18) позволяют найти значения при практических расчетах.
Дадим геометрическую интерпретацию комплексной формы ряда Фурье. Выделим k-тую составляющую спектра сигнала. В комплексной форме k-я составляющая описывается формулой
где и определятся выражениями (2.15).
В комплексной плоскости каждое из слагаемых в (2.19) изображается в виде векторов длиной  , повернутых на угол и относительно вещественной оси и вращающихся в противоположных направлениях с частотой (рис. 2.5).
, повернутых на угол и относительно вещественной оси и вращающихся в противоположных направлениях с частотой (рис. 2.5).
Очевидно, сумма этих векторов дает вектор, расположенный на вещественной оси, длина которого составляет . Но этот вектор соответствует гармонической составляющей


Что касается проекций векторов на мнимую ось, то эти проекции имеют равную длину, но противоположные направления и в сумме дают ноль. А это значит, что сигналы, представленные в комплексной форме (2.16) в действительности являются вещественными сигналами. Иными словами, комплексная форма ряда Фурье является математической абстракцией, весьма удобной при решении целого ряда задач спектрального анализа. Поэтому, иногда спектр, определяемый тригонометрическим рядом Фурье, называют физическим спектром , а комплексной формой ряда Фурье – математическим спектром .
И в заключение рассмотрим вопрос распределения энергии и мощности в спектре периодического сигнала. Для этого воспользуемся равенством Парсеваля (1.42). При разложении сигнала в тригонометрический ряд Фурье выражение (1.42) принимает вид
 .
.
Энергия постоянной составляющей
 ,
,
а энергия k-той гармоники
 .
.
Тогда энергия сигнала
 . (2.20)
. (2.20)
Т.к. средняя мощность сигнала
 ,
,
то с учетом (2.18)
 . (2.21)
. (2.21)
При разложение сигнала в комплексный ряд Фурье выражение (1.42) имеет вид
 ,
,
где  - энергия k-той гармоники.
- энергия k-той гармоники.
Энергия сигнала в этом случае
 ,
,
а его средняя мощность
 .
.
Из приведенных выражений следует, что энергия или средняя мощность k-той спектральной составляющей математического спектра вдвое меньше энергии или мощности соответствующей спектральной составляющей физического спектра. Это обусловлено тем, что физического спектра распределяется поровну между и математического спектра.
| -τ и /2 |
| τ и /2 |
| Т |
| t |
| U 0 |
| S(t) |
Задание №1, группа РИ – 210701
В электронной аппаратуре различного применения широко используются периодические последовательности прямоугольных импульсов. При этом соотношения длительности импульса τ и периода колебания T могут сильно отличаться. Например, колебания, которые вырабатывают тактовые генераторы , задающие «темп» работы компьютеров, характеризуются соизмеримыми значениями τ и T , а импульсы, применяемые в радиолокации, могут быть в сотни раз короче периода. Отношение T /τ называют скважностью импульса , а обратную величину (τ/T ) - коэффициентом заполнения .
Рис. 6. Последовательность прямоугольных импульсов (а) и коэффициенты ряда Фурье (б)
Рассмотрим последовательность прямоугольных импульсов, имеющих амплитуду А , длительность τ и следующих с периодом T (рис. 6, а ). Выберем начало отсчета времени так, как показано на рисунке, то есть, чтобы импульс был симметричен относительно нулевой отметки, и вычислим коэффициенты ряда Фурье (1). Поскольку функция s (t ) при таком положении осей оказывается четной, все b n равны нулю, а для a n получаем:
Ряд Фурье для последовательности прямоугольных импульсов принимает вид:
 (6)
(6)
Значения коэффициентов ряда Фурье, вычисленные по формулам (5), изображены на спектральной диаграмме, показанной на рис. 6, б .
Коэффициенты
a
n
можно связать с функцией
 .
Действительно, они будут пропорциональны
(с множителем
.
Действительно, они будут пропорциональны
(с множителем
 )
значениям функции
)
значениям функции
 при аргументах, соответствующих частотам
гармоник. Это видно, если выражение (5)
переписать так:
при аргументах, соответствующих частотам
гармоник. Это видно, если выражение (5)
переписать так:
 (7)
(7)
Таким
образом, функция типа
 является огибающей
для коэффициентов Фурье-разложения
последовательности прямоугольных
импульсов (см. рис. 6, б
).
Положение нулей огибающей на частотной
оси f
можно найти из условия
является огибающей
для коэффициентов Фурье-разложения
последовательности прямоугольных
импульсов (см. рис. 6, б
).
Положение нулей огибающей на частотной
оси f
можно найти из условия
 или
или ,
где. Первый раз огибающая обращается
в нуль при частотеf
=
1/τ (или ω = 2π/τ). Далее нули огибающей
повторяются при f
= 2/τ, 3/τ, и т. д. Эти частоты могут совпасть
(при целочисленных скважностях
)
с частотами каких-либо гармоник спектра,
и данные частотные составляющие из ряда
Фурье исчезнут. Если скважность - целое
число, периодT
точно кратен длительности импульсов.
Тогда между двумя нулями огибающей
разместятся гармоники спектра в
количестве q
-
1.
,
где. Первый раз огибающая обращается
в нуль при частотеf
=
1/τ (или ω = 2π/τ). Далее нули огибающей
повторяются при f
= 2/τ, 3/τ, и т. д. Эти частоты могут совпасть
(при целочисленных скважностях
)
с частотами каких-либо гармоник спектра,
и данные частотные составляющие из ряда
Фурье исчезнут. Если скважность - целое
число, периодT
точно кратен длительности импульсов.
Тогда между двумя нулями огибающей
разместятся гармоники спектра в
количестве q
-
1.
Каким
образом связаны параметры импульсов
во временном и частотном представлениях
иллюстрирует табл. 2. С увеличением
периода T
гармоники на спектральной диаграмме
сближаются (спектр становится «гуще»).
Однако изменение только периода не
приводит к изменению формы огибающей
амплитудного спектра. Эволюция огибающей
(сдвиг ее нулей) зависит от длительности
импульсов. Здесь показана эволюция
амплитудных спектральных диаграмм для
последовательностей прямоугольных
импульсов, у которых изменяются
длительности импульсов и периоды. По
осям ординат спектральных диаграмм
отложены относительные значения амплитуд
гармоник:
 Они рассчитаны по формулам:
Они рассчитаны по формулам:
 (8)
(8)
Таблица 2. Осциллограммы и спектрограммы последовательностей прямоугольных импульсов

2.5. Спектры хаотических (шумовых) колебаний
Хаотическое колебание s (t ) - это случайный процесс . Каждая его реализация в неизменных условиях не повторяется, является уникальной. В электронике хаотические колебания связаны с шумами - колебаниями токов и напряжений, изменяющихся случайным образом вследствие беспорядочного движения носителей зарядов. В данном контексте хаотические и шумовые колебания считаются синонимами.
Рис. 7. Структурная схема измерения среднего квадрата шумового напряжения
Шумовое колебание можно описать в частотном представлении: ему сопоставляют некую спектральную характеристику, причем для случайного процесса она непрерывна. Теоретические основы спектрального разложения хаотических колебаний изложены в . Не погружаясь в строгую теорию, объясним методику экспериментального исследования статистических параметров шумового напряжения s (t ) по схеме, показанной на рис. 8.
Р ис.
8.
Схема измерения спектральной плотности
интенсивности шумового напряжения
ис.
8.
Схема измерения спектральной плотности
интенсивности шумового напряжения
Пропустим
шумовое напряжение s
(t
)
через фильтр, выделяющий энергию
колебаний в узкой полосе
 вблизи частоты f
.
При соблюдении условия
вблизи частоты f
.
При соблюдении условия
 <<
f
колебание на выходе фильтра будет
напоминать синусоиду с частотой f
.
Однако амплитуда и фаза этой синусоиды
подвержены хаотическим изменениям. С
уменьшением полосы пропускания фильтра
<<
f
колебание на выходе фильтра будет
напоминать синусоиду с частотой f
.
Однако амплитуда и фаза этой синусоиды
подвержены хаотическим изменениям. С
уменьшением полосы пропускания фильтра
 форма выходного колебания все более
приближается к синусоиде. Амплитуда ее
уменьшается, но отношение среднего
квадрата напряжения, прошедшего через
фильтр (
форма выходного колебания все более
приближается к синусоиде. Амплитуда ее
уменьшается, но отношение среднего
квадрата напряжения, прошедшего через
фильтр ( ),
к ширине полосы
),
к ширине полосы
 остается конечным и при последовательном
уменьшении полосы стремится к определенному
пределу W
(f
):
остается конечным и при последовательном
уменьшении полосы стремится к определенному
пределу W
(f
):
Предельную
величину W
(f
)
называют спектральной
плотностью интенсивности
процесса
s
(t
).
Она равна средней интенсивности
гармонических составляющих, приходящихся
на единичный интервал оси частот. При
измерении W
(f
)
используют узкополосный перестраиваемый
фильтр, который можно настроить на любую
частоту в заданном диапазоне измерений.
Шумовое напряжение, прошедшее сквозь
фильтр, подвергают квадратичному
детектированию и усредняют (интегрируют).
В результате получают средний квадрат:
 . Далее по известной полосе фильтра
. Далее по известной полосе фильтра
 вычисляют W
(f
).
Полную
интенсивность процесса
- средний квадрат
вычисляют W
(f
).
Полную
интенсивность процесса
- средний квадрат
 - находят интегрированием спектральных
составляющих шума по всем частотам:
- находят интегрированием спектральных
составляющих шума по всем частотам:
 (10)
(10)
Для подготовки к работе следует изучить в полном объеме данное пособие. Более подробные сведения по теме лабораторной работы можно найти в главе «Частотные спектры электрических колебаний, спектральный анализ» книги .
Периодическая последовательность прямоугольных видеоимпульсов является модулирующей функцией для формирования периодической последовательности прямоугольных радиоимпульсов (ПППВИ), которые являются зондирующими сигналами для обнаружения и измерения координат движущихся целей. Поэтому, по спектру модулирующей функции (ПППВИ), можно относительно просто и быстро и определить спектр зондирующего сигнала (ПППРИ). При отражении зондирующего сигнала от движущейся цели изменяются частоты спектра гармоник несущего колебания (эффект Доплера). Вследствие чего, можно выделить полезный сигнал, отраженный от движущейся цели, на фоне мешающих (помеховых) колебаний, отраженных от неподвижных объектов (местные предметы) или малоподвижных объектов (метеообразования, стаи птиц и др.).
ПППВИ (рис. 1.42) представляет собой совокупность одиночных прямоугольных видеоимпульсов, следующих друг за другом через равные промежутки времени. Аналитическое выражение сигнала.
где – амплитуда импульсов; – длительность импульсов; – период следования импульсов; – частота следования импульсов, ; – скважность.
Для вычисления спектрального состава периодической последовательности импульсов применяют ряд Фурье. При известных спектрах одиночных импульсов, образующих периодическую последовательность, можно воспользоваться связью между спектральной плотностью импульсов и комплексными амплитудами ряда:
Для одиночного прямоугольного видеоимпульса спектральная плотность описывается формулой
Воспользовавшись связью между спектральной плотностью одиночного импульса и комплексными амплитудами ряда, находим
где = 0; ± 1; ± 2; ...
Амплитудно-частотный спектр (рис. 1.43) будет представлен совокупностью составляющих:
при этом положительным значениям соответствуют нулевые начальные фазы, а отрицательным – начальные фазы, равные .
Таким образом, аналитическое выражение ПППВИ будет равно
Из анализа графиков, приведенных на рисунке 1.43 следует:
· Спектр ПППВИ дискретный состоящий из отдельных гармоник с частотой .
· Огибающая АЧС изменяется по закону .
· Максимальное значение огибающей при равно , значение постоянной составляющей .
· Начальные фазы гармоник в пределах нечетных лепестков равны 0, в пределах четных .
· Количество гармоник в пределах каждого лепестка равно .
· Ширина спектра сигнала на уровне 90% энергии сигнала
· База сигнала , поэтому сигнал является простым.
Если изменять длительность импульсов , либо частоту их повторения F (период ), то параметры спектра и его АЧС будет изменяться.
На рисунке 1.43 представлен пример изменения сигнала и его АЧС при увеличении длительности импульса в два раза.
Периодические последовательности прямоугольных видеоимпульсов и их АЧС параметрами , T ,. и , T , изображены на рисунке 1.44.
Из анализа приведенных графиков следует:
1. Для ПППВИ с длительностью импульса :
· Скважность q =4, следовательно, в пределах каждого лепестка сосредоточено 3 гармоники;
· Частота k-ой гармоники ;
· Ширина спектра сигнала на уровне 90% энергии ;
· Постоянная составляющая равна
2. Для ПППВИ с длительностью импульса :
· Скважность q= 2, следовательно, в пределах каждого лепестка находится 1 гармоника;
· Частота k-ой гармоники осталось неизменной ;
· Ширина спектра сигнала на уровне 90% его энергии уменьшилась в 2 раза ;
· Постоянная составляющая увеличилась в 2 раза .
Таким образом, можно сделать вывод, что при увеличении длительности импульса, происходит “сжатие” АЧС вдоль оси ординат (уменьшается ширина спектра сигнала), при этом увеличиваются амплитуды спектральных составляющих. Частоты гармоник не изменяются.
На рисунке 1.44. представлен пример изменения сигнала и его АЧС при увеличении периода следования в 4 раза (уменьшение частоты повторения в 4 раза).
c) ширина спектра сигнала на уровне 90% его энергии не изменилась;
d) постоянная составляющая уменьшилась в 4 раза.
Таким образом, можно сделать вывод, что при увеличении периода следования (уменьшении частоты повторения происходит “сжатие ”) АЧС вдоль оси частот (уменьшаются амплитуды гармоник с увеличением их количества в пределах каждого лепестка). Ширина спектра сигнала при этом не изменяется. Дальнейшее уменьшение частоты повторения (увеличения периода следования) приведет (при ) к уменьшению амплитуд гармоник до бесконечно малых величин. При этом сигнал превратиться в одиночный, соответственно спектр станет сплошным.
Спектральное представление временных функций широко используется в теории связи. Для теоретических и экспериментальных исследований характеристик электрических цепей и передачи сообщений по каналам связи используется различные типы сигналов: гармонические колебания, уровни постоянных напряжений, последовательности прямоугольных и радиоимпульсов и т. д. Особо важную роль в теоретических исследованиях электрических цепей играют вычислительные сигналы в форме единичной функции и импульсной функции (функции Дирака). Определим спектры наиболее распространенных типовых сигналов.
11.1 Спектр последовательности прямоугольных импульсов
Пусть имеется периодическая последовательность импульсов прямоугольной формы периодом Т длительностью импульсов t и и амплитудой А. Аналитическое выражение функции , описывающей импульс на отрезке , имеет вид
 (11.1)
(11.1)
График периодической последовательности импульсов изображен на рисунке 11.1.

Рисунок 11.1
Данная функция является четной, так как ее график симметричен относительно оси ординат. Тогда коэффициенты Фурье это функции вычисляются по формулам (КФТ2), где .

Число представляет собой среднее значение функции за период и называется постоянной составляющей. Частоту называют основной, или первой гармоникой, а частоты k высшими гармониками, где k=2,3,4,…
Построим амплитудный спектр рассматриваемой последовательности прямоугольных импульсов. Так как функция периодическая, то ее амплитудный спектр является линейчатым. Обозначим через расстояние между любыми соседними гармониками. Очевидно, оно равно . Амплитуда k-ой гармоники согласно (11.2) имеет вид
 (11.3)
(11.3)
Найдем отношение между периодом Т и длительностью импульса , при котором амплитуда k-ой гармоники обращается в нуль.
А 2 ≈32В, А 3 ≈15В, А 4 ≈0, А 5 ≈6,36В, А 6 ≈10,5В, А 7 ≈6,36В, А 8 ≈0, А 9 ≈4,95В, А 10 ≈6,37В.
Полученный в результате расчета амплитудный спектр приведен на рисунке 11.2.

Рисунок 11.2
Такой спектр называют линейчатым или дискретным спектром.
Аналогично рассчитаны и построены спектры для q=8 и q=16. Они приведены на рисунках 11.3 и 11.4 соответственно.

Рисунок 11.3

Рисунок 11.4
Из рисунка видно, что чем больше скважность прямоугольных импульсов, тем меньше значение имеет амплитуда первой гармоники, но тем медленнее убывает спектр.
11.2 Спектр одиночного прямоугольного импульса
Рассмотрим Ф (11.1) для случая, когда Т→∞, то есть периодическая последовательность импульсов вырождается в одиночный прямоугольный импульс, длительностью t u .
Аналитическое выражение для этого импульса запишется в виде:
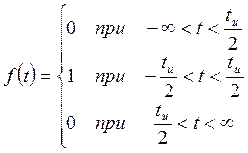
График этой функции изображен на рисунке 11.5.

Рисунок 11.5
В этом случае частота первой гармоники и расстояние между гармониками становится равным 0, следовательно, спектр из дискретного превращается в непрерывный, состоящий из бесконечно большого числа спектральных линий, находящихся на бесконечно малых расстояниях друг от друга. Такой спектр называют сплошным. Отсюда следует важнейшее правило: периодические сигналы порождают дискретные спектры, а непериодические – сплошные (непрерывные).
Спектр прямоугольного одиночного импульса можно найти непосредственно из прямого преобразования Фурье (10.1)
