СВОЈСТВАТА НА ФУНКЦИИТЕ КОНТИНУИРАНИ НА ИНТЕРВЈУ

Да разгледаме некои својства на функциите континуирани на интервал. Овие својства ги прикажуваме без доказ.

Функција y = f(x)повикани континуирано на сегментот [а, б], ако е континуиран во сите внатрешни точки на овој сегмент, и на неговите краеви, т.е. на точките аИ б, е континуирано десно и лево, соодветно.

Теорема 1.Функција континуирана на интервалот [ а, б], барем во една точка од овој сегмент ја зема најголемата вредност и барем во една точка најмалата.

Теоремата вели дека ако функција y = f(x)е континуиран во интервалот [ а, б], тогаш има барем една точка x 1 Î [ а, б] така што вредноста на функцијата f(x)во овој момент ќе биде најголемата од сите нејзини вредности на овој сегмент: f(x 1) ≥ f(x). Слично на тоа, постои таков момент x 2, во која вредноста на функцијата ќе биде најмала од сите вредности на сегментот: f(x 1) ≤ f(x).

Јасно е дека може да има неколку такви точки; на пример, сликата покажува дека функцијата f(x)ја зема најмалата вредност на две точки x 2И x 2 ".

Коментар. Изјавата на теоремата може да стане неточна ако ја земеме предвид вредноста на функцијата на интервалот ( а, б). Навистина, ако ја земеме предвид функцијата y = xна (0, 2), тогаш тој е континуиран на овој интервал, но не ги достигнува ниту најголемите ниту најмалите вредности во него: ги достигнува овие вредности на краевите на интервалот, но краевите не припаѓаат на нашиот домен.

Исто така, теоремата престанува да важи за дисконтинуирани функции. Наведи пример.

Последица.Доколку функцијата f(x)е континуирано на [ а, б], тогаш е ограничен на овој сегмент.

Теорема 2.Нека функцијата y = f(x)е континуиран во интервалот [ а, б] и на краевите на овој сегмент зема вредности на различни знаци, тогаш има барем една точка внатре во сегментот x = C, во која функцијата оди на нула: f(C)= 0, каде што a< C< b

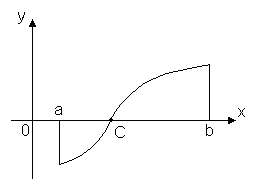
Оваа теорема има едноставно геометриско значење: ако точките на графикот на континуирана функција y = f(x), што одговара на краевите на сегментот [ а, б] лежат на спротивните страни на оската Вол, тогаш овој график ја пресекува оската барем на една точка од отсечката Вол. Дисконтинуираните функции може да го немаат ова својство.

Оваа теорема ја признава следнава генерализација.

Теорема 3 (теорема за средна вредност).Нека функцијата y = f(x)е континуиран во интервалот [ а, б] И f(a) = A, f(b) = B. Потоа за кој било број В, склучен помеѓу АИ Б, постои таква точка во овој сегмент ВÎ [ а, б], Што f(c) = C.

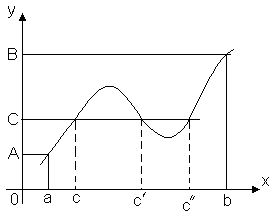
Оваа теорема е геометриски очигледна. Размислете за графикот на функцијата y = f(x). Нека f(a) = A, f(b) = B. Потоа секоја права линија y = C, Каде В– кој било број помеѓу АИ Б, ќе го пресече графикот на функцијата барем во една точка. Апсцисата на пресечната точка ќе биде таа вредност x = C, на која f(c) = C.

Така, континуирана функција, која се движи од една вредност во друга, нужно поминува низ сите средни вредности. Особено:

Последица.Доколку функцијата y = f(x)е континуирано во одреден интервал и ги зема најголемите и најмалите вредности, а потоа на овој интервал ја зема барем еднаш секоја вредност содржана помеѓу неговите најмали и најголеми вредности.

ДЕРИВАТИВ И НЕГОВИ ПРИМЕНИ. ДЕФИНИЦИЈА НА ДЕРИВАТИВ

Да имаме некоја функција y=f(x),дефинирани на одреден интервал. За секоја вредност на аргументот xод овој интервал функцијата y=f(x)има одредено значење.

Размислете за две вредности на аргументот: почетна x 0 и ново x.

Разлика x–x 0 се нарекува со зголемување на аргументот xво точката x 0 и се означува Δx. Така, Δx = x – x 0 (зголемувањето на аргументот може да биде позитивно или негативно). Од оваа еднаквост произлегува дека x=x 0 +Δx, т.е. почетната вредност на променливата доби одредено зголемување. Потоа, ако во точката x 0 вредноста на функцијата беше f(x 0 ), потоа во нова точка xфункцијата ќе ја земе вредноста f(x) = f(x 0 +Δx).

Разлика y–y 0 = f(x) – f(x 0 ) повикани зголемување на функцијата y = f(x)во точката x 0 и се означува со симболот Δy. Така,

Типично почетната вредност на аргументот x 0 се смета за фиксна, а новата вредност x– променлива. Потоа y 0 = f(x 0 ) излегува дека е константна, и y = f(x)– променлива. Инкременти ΔyИ Δxисто така ќе бидат променливи и формулата (1) покажува дека Даје функција на променлива Δx.

Да го креираме односот на зголемувањето на функцијата со зголемувањето на аргументот

Дозволете ни да ја најдеме границата на овој сооднос на Δx→0. Ако оваа граница постои, тогаш се нарекува дериват на оваа функција f(x)во точката x 0 и означува ѓ "(x 0). Значи,

Дериватоваа функција y = f(x)во точката x 0 се нарекува граница на односот на зголемување на функцијата Δ yдо зголемувањето на аргументот Δ x, кога вториот произволно се стреми кон нула.

Забележете дека за иста функција изводот на различни точки xможе да прими различни вредности, т.е. дериватот може да се смета како функција на аргументот x. Оваа функција е назначена ѓ "(x)

Дериватот се означува со симболите ѓ "(x), y", . Специфичната вредност на дериватот во x = aозначено со ѓ "(а) или y "| x=a.

Операција на пронаоѓање на извод на функција f(x)се нарекува диференцијација на оваа функција.

За директно да го пронајдете дериватот по дефиниција, можете да го користите следново: правило на палецот:

Примери.

МЕХАНИЧКО ЧУВСТВО ЗА ДЕРИВАТИВ

Од физиката е познато дека законот за еднообразно движење има форма s = v t, Каде с– патеката патувала до моментот на времето т, v– брзина на еднообразно движење.

Меѓутоа, бидејќи Повеќето движења што се случуваат во природата се нерамномерни, потоа генерално брзината и, следствено, растојанието сќе зависи од времето т, т.е. ќе биде функција на времето.

Значи, нека материјална точка се движи праволиниски во една насока според законот s=s(t).

Ајде да одбележиме одредена точка во времето т 0 . Во овој момент точката го помина патот s=s(t 0 ). Ајде да ја одредиме брзината vматеријална точка во еден момент во времето т 0 .

За да го направите ова, да разгледаме некоја друга точка во времето т 0 + Δ т. Тоа одговара на поминатата патека s =s(t 0 + Δ т). Потоа во одреден временски период Δ тточката ја поминала патеката Δs =s(t 0 + Δ т)–s(t).

Да го разгледаме ставот. Се нарекува просечна брзина во временскиот интервал Δ т. Просечната брзина не може точно да ја карактеризира брзината на движење на точка во моментот т 0 (бидејќи движењето е нерамномерно). За попрецизно да ја изразите оваа вистинска брзина користејќи ја просечната брзина, треба да одвоите пократок временски период Δ т.

Значи, брзината на движење во даден момент во времето т 0 (моментална брзина) е граница на просечна брзина во интервалот од т 0 до т 0 +Δ т, кога Δ т→0:

,

тие. нерамна брзинаова е дериват на поминатото растојание во однос на времето.

ГЕОМЕТРИСКО ЗНАЧЕЊЕ НА ДЕРИВАТ

Прво да ја воведеме дефиницијата за тангента на крива во дадена точка.

Дозволете ни да имаме крива и фиксна точка на неа М 0(види слика) Размислете за друга точка Моваа крива и нацртајте секанта М 0 М. Ако точката Мпочнува да се движи по кривата, а точката М 0останува неподвижен, а потоа секантот ја менува својата позиција. Ако, со неограничено приближување на точката Мпо крива до точка М 0на која било страна секантата има тенденција да зазема положба на одредена права линија М 0 Т, потоа директно М 0 Тнаречена тангента на кривата во дадена точка М 0.

Тоа., тангентадо кривата во дадена точка М 0наречена гранична положба на секантата М 0 Мкога точка Мсе стреми по кривата до точка М 0.

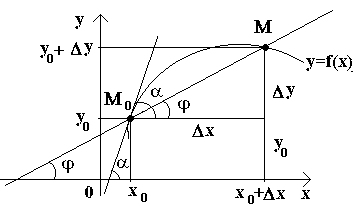
Сега да ја разгледаме континуираната функција y=f(x)и кривата што одговара на оваа функција. По некоја вредност XФункцијата 0 зема вредност y 0 =f(x 0).Овие вредности x 0 и y 0 на кривата одговара на точка M0 (x0; y 0).Ајде да го дадеме аргументот x 0прираст Δ X. Новата вредност на аргументот одговара на зголемената вредност на функцијата y 0 +Δ y=f(x 0 –Δ x). Ја сфаќаме поентата М(х 0+Δ x; y 0+Δ y).Ајде да нацртаме секант М 0 Ма со φ означете го аголот формиран од секанта со позитивната насока на оската Вол. Ајде да создадеме врска и да забележиме дека .

Ако сега Δ x→0, тогаш поради континуитет на функцијата Δ на→0, а со тоа и точката М, движејќи се по крива, се приближува до точката без ограничување М 0. Потоа секантот М 0 Мќе има тенденција да заземе позиција на тангента на кривата во точката М 0, и аголот φ→α на Δ x→0, каде α го означува аголот помеѓу тангентата и позитивната насока на оската Вол. Бидејќи функцијата tan φ континуирано зависи од φ за φ≠π/2, тогаш за φ→α tan φ → tan α и, според тоа, наклонот на тангентата ќе биде:

тие. f" (x)= tg α .

Така, геометриски y" (x 0)го претставува наклонот на тангентата на графикот на оваа функција во точката x 0, т.е. за дадена вредност на аргументот x, изводот е еднаков на тангентата на аголот формиран од тангентата на графикот на функцијата f(x)во соодветната точка M 0 (x; y)со насока на позитивна оска Вол.

Пример.Најдете го наклонот на тангентата на кривата y = x 2 во точка М(-1; 1).

Веќе видовме порано дека ( x 2)" = 2X. Но, аголниот коефициент на тангентата на кривата е tan α = y"| x=-1 = – 2.

РАЗЛИЧНОСТ НА ФУНКЦИИТЕ. КОНТИНУИТЕТ НА РАЗЛИЧНА ФУНКЦИЈА

Функција y=f(x)повикани диференцијабилнаво одреден момент x 0 ако има одреден извод во оваа точка, т.е. ако границата на врската постои и е конечна.

Ако функцијата е диференцијабилна во секоја точка од одреден сегмент [ А; б] или интервал ( А; б), тогаш велат дека таа диференцијабилнана сегментот [ А; б] или, соодветно, во интервалот ( А; б).

Валидна е следната теорема, со која се воспоставува врска помеѓу диференцијабилните и континуираните функции.

Теорема.Доколку функцијата y=f(x)може да се разликува во одреден момент x 0, тогаш тоа е континуирано во оваа точка.

Така, од диференцијабилноста на функцијата следи нејзиниот континуитет.

Доказ. Ако , Тоа

,

каде α е бесконечно мала големина, т.е. количество кое се стреми кон нула како Δ x→0. Но тогаш

Δ y=ѓ "(x 0) Δ x+αΔ x=> Δ y→0 на Δ x→0, т.е. f(x) – f(x 0)→0 во x→x 0 , што значи дека функцијата f(x)континуирано во една точка x 0 . Q.E.D.

Така, функцијата не може да има извод во точките на дисконтинуитет. Обратно не е точно: има континуирани функции кои не се диференцијабилни во некои точки (односно, немаат извод во овие точки).

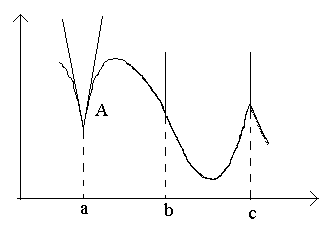
Размислете за точките на сликата а, б, в.

Во точката ана Δ x→0 односот нема ограничување (бидејќи едностраните граници се различни за Δ x→0–0 и Δ x→0+0). Во точката Аграфикон нема дефинирана тангента, но има две различни еднонасочни тангенти со косини До 1 и До 2. Овој тип на точка се нарекува аголна точка.

Во точката бна Δ xОдносот →0 е константен знак бескрајно голема количина. Функцијата има бесконечен извод. Во овој момент графикот има вертикална тангента. Тип на точка - „точка на флексија“ на вертикална тангента.

Во точката ведностраните деривати се бескрајно големи количини на различни знаци. Во овој момент графикот има две споени вертикални тангенти. Тип - „повратна точка“ со вертикална тангента - посебен случај на аголна точка.

Сликите подолу покажуваат каде функцијата може да ја достигне својата најмала и најголема вредност. На левата слика, најмалите и најголемите вредности се фиксирани во точките на локалниот минимум и максимум на функцијата. На десната слика - на краевите на сегментот.

Доколку функцијата y = ѓ(x) е континуиран во интервалот [ а, б] , тогаш стигнува на овој сегмент најмалку И највисоки вредности . Ова, како што веќе споменавме, може да се случи или во екстремни точки, или на краевите на сегментот. Затоа, да се најде најмалку И најголемите вредности на функцијата , континуирано на интервалот [ а, б] , треба да ги пресметате неговите вредности во сите критични точкии на краевите на отсечката, а потоа изберете ги најмалите и најголемите од нив.

Нека, на пример, сакате да ја одредите најголемата вредност на функцијата ѓ(x) на сегментот [ а, б] . За да го направите ова, треба да ги најдете сите негови критични точки што лежат на [ а, б] .

Критична точка наречена точка во која дефинирана функција, и неа дериватили еднакво на нула или не постои. Потоа треба да ги пресметате вредностите на функцијата во критичните точки. И, конечно, треба да се споредат вредностите на функцијата во критичните точки и на краевите на сегментот ( ѓ(а) И ѓ(б)). Најголемиот од овие бројки ќе биде најголемата вредност на функцијата на сегментот [а, б] .

Проблеми со наоѓање најмалите функциски вредности .

Заедно ги бараме најмалите и најголемите вредности на функцијата

Пример 1. Најдете ги најмалите и најголемите вредности на функцијата на сегментот [-1, 2] .

Решение. Најдете го изводот на оваа функција. Да го изедначиме изводот со нула () и да добиеме две критични точки: и . За да се најдат најмалите и најголемите вредности на функцијата на даден сегмент, доволно е да се пресметаат нејзините вредности на краевите на сегментот и во точката, бидејќи точката не припаѓа на отсечката [-1, 2]. Овие вредности на функции се: , , . Го следи тоа најмала функционална вредност(означено со црвено на графиконот подолу), еднакво на -7, се постигнува на десниот крај на отсечката - во точката , и најголем(исто така црвено на графикот), е еднакво на 9, - во критичната точка.

Ако функцијата е континуирана во одреден интервал и овој интервал не е отсечка (туку е, на пример, интервал; разликата помеѓу интервалот и отсечката: граничните точки на интервалот не се вклучени во интервалот, туку граничните точки на сегментот се вклучени во сегментот), тогаш меѓу вредностите на функцијата можеби нема да има најмала и најголема. Така, на пример, функцијата прикажана на сликата подолу е континуирана на ]-∞, +∞[ и нема најголема вредност.

Меѓутоа, за кој било интервал (затворен, отворен или бесконечен), следново својство на континуирани функции е точно.

За самопроверка за време на пресметките, можете да користите онлајн калкулатор за деривати .

Пример 4. Најдете ги најмалите и најголемите вредности на функцијата на сегментот [-1, 3] .

Решение. Го наоѓаме изводот на оваа функција како извод на количникот:

.

Изводот го изедначуваме со нула, што ни дава една критична точка: . Припаѓа на сегментот [-1, 3] . За да ги најдеме најмалите и најголемите вредности на функцијата на даден сегмент, ги наоѓаме нејзините вредности на краевите на сегментот и на пронајдената критична точка:

Ајде да ги споредиме овие вредности. Заклучок: еднаков на -5/13, во точка и највисока вредностеднакво на 1 во точка .

Продолжуваме заедно да ги бараме најмалите и најголемите вредности на функцијата

Има наставници кои на тема пронаоѓање на најмалите и најголемите вредности на функцијата не им даваат на учениците примери за решавање кои се посложени од оние кои штотуку беа дискутирани, односно оние во кои функцијата е полином или дропка, чиј броител и именител се полиноми. Но, ние нема да се ограничиме на такви примери, бидејќи меѓу наставниците има и такви кои сакаат да ги принудат учениците да размислуваат целосно (табела со деривати). Затоа ќе се користат логаритамската и тригонометриската функција.

Пример 8. Најдете ги најмалите и најголемите вредности на функцијата на сегментот .

Решение. Изводот на оваа функција го наоѓаме како дериват на производот :

Изводот го изедначуваме со нула, што дава една критична точка: . Припаѓа на сегментот. За да ги најдеме најмалите и најголемите вредности на функцијата на даден сегмент, ги наоѓаме нејзините вредности на краевите на сегментот и на пронајдената критична точка:

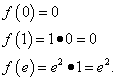
Резултат од сите дејства: функцијата ја достигнува својата минимална вредност, еднакво на 0, во точката и во точката и највисока вредност, еднакви д², во точката.

За самопроверка за време на пресметките, можете да користите онлајн калкулатор за деривати .

Пример 9. Најдете ги најмалите и најголемите вредности на функцијата на сегментот .

Решение. Најдете го изводот на оваа функција:

Изводот го изедначуваме со нула:

Единствената критична точка му припаѓа на сегментот. За да ги најдеме најмалите и најголемите вредности на функцијата на даден сегмент, ги наоѓаме нејзините вредности на краевите на сегментот и на пронајдената критична точка:

Заклучок: функцијата ја достигнува својата минимална вредност, еднакво на , во точката и највисока вредност, еднакви , во точката .

Кај применетите екстремни проблеми, наоѓањето на најмалите (максимални) вредности на функцијата, по правило, се сведува на наоѓање на минимум (максимум). Но, не се од поголем практичен интерес самите минимуми или максимални, туку оние вредности на аргументот со кои се постигнуваат. При решавање на применетите проблеми, се јавува дополнителна тешкотија - составување функции кои го опишуваат феноменот или процесот што се разгледува.

Пример 10.Резервоарот со капацитет од 4, кој има форма на паралелепипед со квадратна основа и отворен на врвот, мора да се конзервира. Која големина треба да биде резервоарот за да се користи најмалку материјал за покривање?

Решение. Нека x- основната страна, ч- висина на резервоарот, С- неговата површина без покривка, В- нејзиниот волумен. Површината на резервоарот се изразува со формулата, т.е. е функција од две променливи. Да се ​​изрази Скако функција на една променлива го користиме фактот дека , од каде . Замена на пронајдениот израз чво формулата за С:

Ајде да ја испитаме оваа функција до крајност. Таа е дефинирана и диференцијабилна насекаде во ]0, +∞[ и

.

Изводот го изедначуваме со нула () и ја наоѓаме критичната точка. Дополнително, кога изводот не постои, но оваа вредност не е вклучена во доменот на дефиниција и затоа не може да биде екстремна точка. Значи, ова е единствената критична точка. Ајде да го провериме за присуство на екстремум користејќи го вториот доволен знак. Ајде да го најдеме вториот извод. Кога вториот извод е поголем од нула (). Тоа значи дека кога функцијата ќе достигне минимум . Од ова минимумот е единствениот екстремум на оваа функција, тоа е нејзината најмала вредност. Значи, страната на основата на резервоарот треба да биде 2 m, а нејзината висина треба да биде .

За самопроверка за време на пресметките, можете да користите

Од практична гледна точка, најголем интерес е да се користи изводот за да се најдат најголемите и најмалите вредности на функцијата. Со што е ова поврзано? Максимизирање на профитот, минимизирање на трошоците, одредување на оптимално оптоварување на опремата... Со други зборови, во многу области од животот мораме да решаваме проблеми со оптимизирање на некои параметри. И ова се задачи за наоѓање на најголемите и најмалите вредности на функцијата.

Треба да се забележи дека најголемите и најмалите вредности на функцијата обично се бараат на одреден интервал X, кој е или целиот домен на функцијата или дел од доменот на дефиниција. Самиот интервал X може да биде сегмент, отворен интервал , бесконечен интервал.

Во оваа статија ќе зборуваме за наоѓање на најголемите и најмалите вредности на експлицитно дефинирана функција на една променлива y=f(x).

Навигација на страница.

Најголемата и најмалата вредност на функцијата - дефиниции, илустрации.

Ајде накратко да ги разгледаме главните дефиниции.

Најголемата вредност на функцијата тоа за било кој нееднаквоста е вистина.

Најмалата вредност на функцијата y=f(x) на интервалот X се нарекува таква вредност тоа за било кој нееднаквоста е вистина.

Овие дефиниции се интуитивни: најголемата (најмалата) вредност на функцијата е најголемата (најмалата) прифатена вредност на интервалот што се разгледува кај апсцисата.

Стационарни точки- ова се вредностите на аргументот при кој изводот на функцијата станува нула.

Зошто ни се потребни неподвижни точки кога ги наоѓаме најголемите и најмалите вредности? Одговорот на ова прашање го дава теоремата на Ферма. Од оваа теорема произлегува дека ако диференцијабилната функција има екстремум (локален минимум или локален максимум) во одредена точка, тогаш оваа точка е стационарна. Така, функцијата често ја зема својата најголема (најмала) вредност на интервалот X во една од стационарни точки од овој интервал.

Исто така, функцијата често може да ги преземе своите најголеми и најмали вредности во точките во кои не постои првиот извод на оваа функција, а самата функција е дефинирана.

Ајде веднаш да одговориме на едно од најчестите прашања на оваа тема: „Дали е секогаш можно да се одреди најголемата (најмалата) вредност на функцијата“? Не, не секогаш. Понекогаш границите на интервалот X се совпаѓаат со границите на доменот на дефинирање на функцијата, или интервалот X е бесконечен. А некои функции во бесконечност и на границите на доменот на дефиниција можат да земат и бесконечно големи и бесконечно мали вредности. Во овие случаи, ништо не може да се каже за најголемата и најмалата вредност на функцијата.

За јасност, ќе дадеме графичка илустрација. Погледнете ги сликите и многу ќе ви стане појасно.

На сегментот

На првата слика, функцијата ги зема најголемите (max y) и најмалите (min y) вредности во стационарни точки лоцирани во сегментот [-6;6].

Размислете за случајот прикажан на втората слика. Ајде да го смениме сегментот во . Во овој пример, најмалата вредност на функцијата се постигнува во стационарна точка, а најголемата во точката со апсциса што одговара на десната граница на интервалот.

На слика 3, граничните точки на отсечката [-3;2] се апсцисите на точките што одговараат на најголемата и најмалата вредност на функцијата.

На отворен интервал

На четвртата слика, функцијата ги зема најголемите (max y) и најмалите (min y) вредности во стационарни точки лоцирани во отворениот интервал (-6;6).

На интервалот, не може да се извлечат заклучоци за најголемата вредност.

Во бесконечноста

Во примерот прикажан на седмата слика, функцијата ја зема најголемата вредност (max y) во неподвижна точка со апсциса x=1, а најмалата вредност (min y) се постигнува на десната граница на интервалот. Во минус бесконечност, вредностите на функциите асимптотички се приближуваат до y=3.

Во текот на интервалот, функцијата не ја достигнува ниту најмалата ниту најголемата вредност. Како што x=2 се приближува оддесно, вредностите на функцијата имаат тенденција кон минус бесконечност (линијата x=2 е вертикална асимптота), а како што апсцисата се стреми кон плус бесконечност, вредностите на функцијата асимптотички се приближуваат до y=3. Графичка илустрација на овој пример е прикажана на Слика 8.

Алгоритам за наоѓање на најголемите и најмалите вредности на континуирана функција на сегмент.

Дозволете ни да напишеме алгоритам кој ни овозможува да ги најдеме најголемите и најмалите вредности на функцијата на сегмент.

1. Го наоѓаме доменот на дефинирање на функцијата и проверуваме дали го содржи целиот сегмент.
2. Ги наоѓаме сите точки во кои не постои првиот извод и кои се содржани во отсечката (обично такви точки се среќаваат во функции со аргумент под знакот на модулот и во функции на моќност со фракционо-рационален експонент). Ако нема такви точки, тогаш преминете на следната точка.
3. Ги одредуваме сите стационарни точки што спаѓаат во сегментот. За да го направите ова, го изедначуваме со нула, ја решаваме добиената равенка и избираме соодветни корени. Ако нема стационарни точки или ниедна од нив не падне во сегментот, тогаш преминете на следната точка.
4. Ги пресметуваме вредностите на функцијата во избрани стационарни точки (ако има), во точки во кои првиот извод не постои (ако има), како и во x=a и x=b.
5. Од добиените вредности на функцијата, ги избираме најголемите и најмалите - тие ќе бидат потребните најголеми и најмали вредности на функцијата, соодветно.

Ајде да го анализираме алгоритмот за решавање на пример за да ги најдеме најголемите и најмалите вредности на функцијата на сегмент.

Пример.

Најдете ја најголемата и најмалата вредност на функцијата

• на сегментот;
• на сегментот [-4;-1] .

Решение.

Доменот на дефиниција на функцијата е целото множество реални броеви, со исклучок на нула, т.е. Двата сегменти спаѓаат во доменот на дефиниција.

Најдете го изводот на функцијата во однос на:

Очигледно, изводот на функцијата постои во сите точки на отсечките и [-4;-1].

Од равенката одредуваме неподвижни точки. Единствениот вистински корен е x=2. Оваа неподвижна точка спаѓа во првиот сегмент.

За првиот случај, ги пресметуваме вредностите на функцијата на краевите на сегментот и во стационарната точка, односно за x=1, x=2 и x=4:

Затоа, најголемата вредност на функцијата се постигнува при x=1, а најмала вредност – на x=2.

За вториот случај, ги пресметуваме вредностите на функциите само на краевите на сегментот [-4;-1] (бидејќи не содржи ниту една стационарна точка):

Решение.

Да почнеме со доменот на функцијата. Квадратниот трином во именителот на дропката не смее да исчезне:

Лесно е да се провери дали сите интервали од изјавата за проблемот припаѓаат на доменот на дефинирање на функцијата.

Ајде да ја разликуваме функцијата:

Очигледно, изводот постои низ целиот домен на дефинирање на функцијата.

Ајде да најдеме неподвижни точки. Изводот оди на нула во. Оваа неподвижна точка спаѓа во интервалите (-3;1] и (-3;2).

Сега можете да ги споредите резултатите добиени во секоја точка со графикот на функцијата. Сините линии со точки означуваат асимптоти.

Во овој момент можеме да завршиме со наоѓање на најголемите и најмалите вредности на функцијата. Алгоритмите дискутирани во оваа статија ви овозможуваат да добиете резултати со минимум дејства. Сепак, може да биде корисно прво да се одредат интервалите на зголемување и намалување на функцијата и дури потоа да се извлечат заклучоци за најголемите и најмалите вредности на функцијата на кој било интервал. Ова дава појасна слика и ригорозно оправдување за резултатите.

Дефиниција3 . 3 Нека е некоја функција, нејзиниот домен на дефиниција и некој (отворен) интервал (можеби со и/или ) 7 . Да ја повикаме функцијата континуирано на интервалот, ако е континуиран во која било точка, односно за која било што постои (во скратена форма:

Нека сега е (затворен) сегмент во . Да ја повикаме функцијата континуирано на сегментот, ако е континуирано на интервалот, континуирано надесно во точката и континуирано налево во точката, т.е

Пример3 . 13 Размислете за функцијата (Heaviside функција) на сегментот , . Тогаш тој е континуиран на сегментот (и покрај тоа што во точката има дисконтинуитет од прв вид).

Сл. 3.15 График на функцијата Хевисајд

Слична дефиниција може да се даде за полуинтервали на формата и , вклучувајќи случаи и . Сепак, можеме да ја генерализираме оваа дефиниција за случајот на произволно подмножество на следниов начин. Прво да го претставиме концептот индуциранадо основи: нека е основа чии завршетоци имаат непразни пресеци со . Да го означиме и да го разгледаме множеството од сите . Тогаш е лесно да се провери дали сетот ќе биде основата. Така, за основите , и , каде , и се основите на непродупчените двострани (лево, десно, соодветно) соседства на точка (видете ја нивната дефиниција на почетокот на тековното поглавје).

Дефиниција3 . 4 Да ја повикаме функцијата континуирано на сетот, Ако

Лесно е да се види дека тогаш и во оваа дефиниција се совпаѓа со оние дадени погоре конкретно за интервалот и сегментот.

Потсетете се дека сите елементарни функции се континуирани во сите точки од нивните домени на дефиниција и, според тоа, континуирани на сите интервали и отсечки што лежат во нивните домени на дефиниција.

Бидејќи континуитетот на интервал и отсечка е дефиниран точкастично, важи теоремата, што е непосредна последица на теоремата 3.1:

Теорема3 . 5 Нека И -- функции и -- интервал или сегмент што лежи во . Нека И континуирано за . Потоа функциите , , континуирано за . Доколку дополнително пред сите , потоа функцијата исто така е континуирано вклучено .

Следното тврдење следи од оваа теорема, исто како и од теорема 3.1 - предлог 3.3:

Понуда3 . 4 Еден куп сите функции континуирани на интервал или сегмент -- ова е линеарен простор:

Посложено својство на континуирана функција се изразува со следнава теорема.

Теорема3 . 6 (за коренот на континуирана функција) Нека функцијата континуирано на сегментот , и И -- број на различни знаци. (За дефинитивно, ќе го претпоставиме тоа , А .) Тогаш има барем една таква вредност , Што (односно има барем еден корен равенки ).

Доказ. Ајде да погледнеме во средината на сегментот. Тогаш тоа е или, или, или. Во првиот случај се наоѓа коренот: ова е . Во преостанатите два случаи, земете го во предвид оној дел од сегментот на чии краеви функцијата зема вредности на различни знаци: во случај или во случај . Избраната половина од отсечката ја означуваме со и ја применуваме истата постапка: подели ја на две половини и , каде , и најде . Во случај да се најде коренот; во случајот понатаму да го разгледаме сегментот , во случај - сегмент итн.

Сл. 3.16 Последователни делби на отсечка на половина

Добиваме дека или во одреден чекор ќе се најде коренот или ќе се конструира систем на вгнездени сегменти

во кој секој следен сегмент е долг половина од претходниот. Низата не се намалува и е ограничена одозгора (на пример, со бројот); затоа (со теорема 2.13), тој има граница. Последователија - нерастечки и ограничен подолу (на пример, со бројот ); тоа значи дека има ограничување. Бидејќи должините на отсечките формираат опаѓачка геометриска прогресија (со именител ), тие имаат тенденција на 0, и , тоа е . Ајде да го ставиме сега. Потоа

И

бидејќи функцијата е континуирана. Меѓутоа, со конструкција на низите и , и , така што, со теоремата за преминување на границата во неравенството (теорема 2.7), и , тоа е, и . Ова значи дека и е коренот на равенката.

Пример3 . 14 Размислете за функцијата на сегментот. Бидејќи и се броеви на различни знаци, функцијата се претвора во 0 во одреден момент од интервалот. Ова значи дека равенката има корен.

Сл.3.17 Графички приказ на коренот на равенката

Докажаната теорема всушност ни дава начин да го најдеме коренот, барем приближен, со кој било степен на точност однапред наведен. Ова е методот на делење на сегмент на половина, опишан во доказот на теоремата. Подолу ќе се запознаеме со овој и со други, поефикасни, методи за приближно наоѓање на коренот, откако ќе ги проучиме концептот и својствата на дериватот.

Забележете дека теоремата не наведува дека ако се исполнети нејзините услови, тогаш коренот е единствен. Како што покажува следната слика, може да има повеќе од еден корен (на сликата има 3).

Сл. 3.18 Неколку корени на функција која зема вредности на различни знаци на краевите на сегментот

Меѓутоа, ако функцијата монотоно се зголемува или монотоно се намалува на сегмент, на чии краеви зема вредности на различни знаци, тогаш коренот е единствен, бидејќи строго монотона функција ја зема секоја нејзина вредност во точно една точка. , вклучувајќи ја и вредноста 0.

Сл. 3.19 Монотона функција не може да има повеќе од еден корен

Непосредна последица на теоремата за коренот на континуирана функција е следнава теорема, која сама по себе е многу важна во математичката анализа.

Теорема3 . 7 (за средната вредност на континуирана функција) Нека функцијата континуирано на сегментот И (за дефинитивно ќе го претпоставиме тоа ). Нека -- некој број лежи помеѓу И . Потоа, постои таква точка , Што .

Сл. 3.20 Континуираната функција зема која било средна вредност

Доказ. Размислете за функцијата помошник , Каде . Потоа И . Функцијата е очигледно континуирана, а според претходната теорема постои точка таква што . Но, оваа еднаквост значи дека.

Забележете дека ако функцијата не е континуирана, тогаш може да не ги земе сите средни вредности. На пример, функцијата Heaviside (види Пример 3.13) ги зема вредностите, но никаде, вклучително и во интервалот, не зема, да речеме, средна вредност. Факт е дека функцијата Heaviside има дисконтинуитет во точка која лежи точно во интервалот.

За понатамошно проучување на својствата на функциите континуирани на интервал, ќе ни треба следново суптилно својство на системот на реални броеви (веќе го споменавме во Поглавје 2 во врска со теоремата за границата на ограничена функција монотоно растечка): секое множество ограничено подолу (односно, такво што за сите и некои; бројот се нарекува долниот рабкомплети) достапни точниот долен раб, односно најголемиот од бројките таков што за сите . Слично на тоа, ако множеството е ограничено погоре, тогаш има точната горна граница: ова е најмалиот од горните лица(за што за сите).

Сл. 3.21 Долните и горните граници на ограниченото множество

Ако , тогаш постои нерастечка низа од точки што се стреми кон . На ист начин, ако , тогаш постои ненамалувачка низа од точки што се стреми кон .

Ако точка припаѓа на множеството, тогаш тоа е најмалиот елемент од ова множество: ; слично ако , Тоа .

Дополнително, за понатаму ќе ни треба следново

Лема3 . 1 Нека -- континуирана функција на сегмент , и многу тие точки , во која (или , или ) не е празна. Потоа во изобилство има најмала вредност , така што пред сите .

Сл. 3.22 Најмалиот аргумент со кој функцијата ја зема одредената вредност

Доказ. Бидејќи е ограничено множество (тоа е дел од сегмент), има инфимум. Тогаш постои низа што не се зголемува , , таква што за . Згора на тоа, по дефиниција за множество. Затоа, поминувајќи до границата, добиваме, од една страна,

а од друга страна, поради континуитетот на функцијата,

Ова значи , значи точката припаѓа на множеството и .

Во случај кога множеството е дефинирано со неравенката, имаме за сите и со теоремата за преминување на границата во неравенката ја добиваме

од каде што значи дека и . Слично, во случај на нееднаквост, преминувањето до границата во неравенството дава

од каде и.

Теорема3 . 8 (за границата на континуирана функција) Нека функцијата континуирано на сегментот . Потоа ограничен на , односно постои таква константа , Што пред сите .

Сл. 3.23 Функцијата континуирана на сегмент е ограничена

Доказ. Да го претпоставиме спротивното: нека не се ограничува, на пример, одозгора. Тогаш сите множества , , , не се празни. Според претходната лема, секое од овие множества има најмала вредност, . Да го покажеме тоа

Навистина, . Ако некоја точка од , на пример, лежи помеѓу и , тогаш

односно средна вредност помеѓу и . Ова значи, според теоремата за средната вредност на континуирана функција, постои точка таква што , И . Но, спротивно на претпоставката дека - најмалата вредност на множеството. Следи дека за сите .

На ист начин, дополнително е докажано дека за сите , за сите итн. Значи, растечката низа е ограничена погоре со бројот . Затоа постои. Од континуитетот на функцијата произлегува дека постои , Но на , така што нема ограничување. Добиената контрадикција докажува дека функцијата е ограничена погоре.

На сличен начин се докажува дека е ограничена одоздола, што го подразбира исказот на теоремата.

Очигледно, невозможно е да се ослабат условите на теоремата: ако функцијата не е континуирана, тогаш не мора да биде ограничена на интервал (ја даваме како пример функцијата

на сегментот. Оваа функција не е ограничена на интервалот, бидејќи во има точка на дисконтинуитет од втор вид, таква што во . Исто така, невозможно е да се замени сегмент во состојбата на теоремата со интервал или полуинтервал: како пример, разгледајте ја истата функција на полуинтервал. Функцијата е континуирана на овој полуинтервал, но неограничена, поради фактот што на .

Пронаоѓањето на најдобрите константи што можат да се користат за ограничување на функцијата од горе и долу на даден интервал природно нè води до проблемот да го најдеме минимумот и максимумот на континуирана функција на овој интервал. Можноста за решавање на овој проблем е опишана со следната теорема.

Теорема3 . 9 (за постигнување екстремум со континуирана функција) Нека функцијата континуирано на сегментот . Потоа, постои точка , така што пред сите (тоа е -- минимална точка: ), и има поента , така што пред сите (тоа е -- максимална точка: ). Со други зборови, минимум и максимум 8 вредности на континуирана функција на сегмент постојат и се постигнуваат во одредени точки И овој сегмент.

Сл. 3.24 Непрекината функција на сегмент достигнува максимум и минимум

Доказ. Бидејќи, според претходната теорема, функцијата е ограничена со горе, тогаш постои точна горна граница за вредностите на функцијата со -- број . Така, множествата ,..., ,..., не се празни, а според претходната лема ги содржат најмалите вредности: , . Тие не се намалуваат (оваа изјава се докажува на ист начин како и во претходната теорема):

и се ограничени одозгора со . Според тоа, според теоремата за граница на монотона ограничена низа, постои граница бидејќи , тогаш

со теоремата за преминување на границата во нееднаквост, односно . Но, со сите, вклучително и. Од ова излегува дека, односно максимумот на функцијата е постигнат во точката.

На сличен начин се докажува и постоењето на минимален поен.

Во оваа теорема, како и во претходната, невозможно е да се ослабат условите: ако функцијата не е континуирана, тогаш може да не ја достигне својата максимална или минимална вредност на сегментот, дури и ако е ограничена. На пример, да ја земеме функцијата

на сегментот. Оваа функција е ограничена на интервалот (очигледно) и , сепак, не ја зема вредноста 1 во ниту една точка од сегментот (забележете дека , не 1). Факт е дека оваа функција има дисконтинуитет од првиот вид во точката , така што на границата не е еднаква на вредноста на функцијата во точката 0. Понатаму, континуирана функција дефинирана на интервал или друго множество што не е затворен сегмент (на полу-интервал, полу-оска) исто така не може да зема екстремни вредности. Како пример, разгледајте ја функцијата на интервалот. Очигледно е дека функцијата е континуирана и дека и, сепак, функцијата не ја зема ниту вредноста 0 ниту вредноста 1 во која било точка од интервалот. Ајде да ја разгледаме и функцијата на оската на оската. Оваа функција е континуирана вклучена, се зголемува, ја зема својата минимална вредност 0 во точката, но не зема максимална вредност во ниту една точка (иако е ограничена од горе со бројот и

Дефиниција. Доколку функцијата ѓ(x) се дефинира на интервалот [ а, б], е континуиран во секоја точка од интервалот ( а, б), во точка аконтинуирано десно, во точката бе континуирано лево, тогаш велиме дека функцијата ѓ(x) континуирано на сегментот [а, б].

Со други зборови, функцијата ѓ(x) е континуирано на интервалот [ а, б], доколку се исполнети три услови:

1) "x 0 Î( а, б): ѓ(x) = ѓ(x 0);

2) ѓ(x) = ѓ(а);

3) ѓ(x) = ѓ(б).

За функциите кои се континуирани на интервал, разгледуваме некои својства, кои ги формулираме во форма на следните теореми, без да изведуваме докази.

Теорема 1. Доколку функцијата ѓ(x) е континуирано на интервалот [ а, б], тогаш ги достигнува своите минимални и максимални вредности на овој сегмент.

Оваа теорема наведува (сл. 1.15) дека на сегментот [ а, б] постои таква точка x 1 тоа ѓ(x 1) £ ѓ(x) за се xод [ а, б] и дека има поента x 2 (x 2 О[ а, б]) така што " xÎ[ а, б] (ѓ(x 2)³ ѓ(x)).

Значење ѓ(x 1) е најголема за дадена функција на [ а, б], А ѓ(x 2) – најмал. Да означиме: ѓ(x 1) = М, ѓ(x 2) =м. Од ѓ(x) важи нееднаквоста: xÎ[ а, б] м£ ѓ(x) £ М, тогаш ја добиваме следната последица од теорема 1.

Последица. Доколку функцијата ѓ(x) е континуирано на интервал, тогаш е ограничен на овој интервал.

Теорема 2. Доколку функцијата ѓ(x) е континуирано на интервалот [ а, б] и на краевите на сегментот зема вредности на различни знаци, тогаш постои таква внатрешна точка x 0 сегмент [ а, б], во која функцијата се претвора во 0, т.е. $ x 0 Î ( а, б) (ѓ(x 0) = 0).

Оваа теорема вели дека графикот на функцијата y = f(x), континуирано на интервалот [ а, б], ја пресекува оската Волбарем еднаш ако вредностите ѓ(а) И ѓ(б) имаат спротивни знаци. Значи, (сл. 1.16) ѓ(а) > 0, ѓ(б) < 0 и функция ѓ(x) станува 0 во поени x 1 , x 2 , x 3 .

Теорема 3. Нека функцијата ѓ(x) е континуирано на интервалот [ а, б], ѓ(а) = А, ѓ(б) = БИ А¹ Б. (Сл. 1.17). Потоа за кој било број В, затворен помеѓу броевите АИ Б, постои таква внатрешна точка x 0 сегмент [ а, б], Што ѓ(x 0) = В.

Последица. Доколку функцијата ѓ(x) е континуирано на интервалот [ а, б], м– најмала вредност ѓ(x), М– најголема вредност на функцијата ѓ(x) на сегментот [ а, б], тогаш функцијата зема (барем еднаш) која било вредност м, склучен помеѓу мИ М, а со тоа и сегментот [ м, М] е множество од сите вредности на функции ѓ(x) на сегментот [ а, б].

Забележете дека ако функцијата е континуирана на интервалот ( а, б) или има на сегментот [ а, б] точки на дисконтинуитет, тогаш теоремите 1, 2, 3 за таква функција престануваат да бидат вистинити.

Како заклучок, разгледајте ја теоремата за постоење на инверзна функција.

Теорема 4. Нека ѓ(x) е континуирано на интервалот X, се зголемува (или се намалува) за Xи има низа вредности Y. Потоа за функцијата y = f(x) постои инверзна функција x= ј(y), дефиниран на интервалот Y, континуирано и зголемување (или намалување) за Yсо повеќе значења X.

Коментар. Нека функцијата x= ј(y) е инверзна на функцијата ѓ(x). Бидејќи аргументот обично се означува со x, и функцијата преку y, потоа во форма ја запишуваме инверзната функција y =ј(x).

Пример 1. Функција y = x 2 (сл. 1.8, а) на сетот X= }