PROPRIETÀ DELLE FUNZIONI CONTINUA IN UN COLLOQUIO

Consideriamo alcune proprietà delle funzioni continue su un intervallo. Presentiamo queste proprietà senza dimostrazione.

Funzione y = f(x) chiamato continuo sul segmento [UN, B], se è continua in tutti i punti interni di questo segmento, e alle sue estremità, cioè in punti UN E B, è continua rispettivamente a destra e a sinistra.

Teorema 1. Una funzione continua sull'intervallo [ UN, B], almeno in un punto di questo segmento assume il valore maggiore e almeno in un punto il valore minore.

Il teorema afferma che se una funzione y = f(x)è continua nell'intervallo [ UN, B], allora c'è almeno un punto x1 Î [ UN, B] tale che il valore della funzione f(x) a questo punto sarà il più grande di tutti i suoi valori su questo segmento: f(x1) ≥ f(x). Allo stesso modo, c'è un punto del genere x2, in cui il valore della funzione sarà il più piccolo di tutti i valori sul segmento: f(x1) ≤ f(x).

È chiaro che potrebbero esserci diversi punti di questo tipo; ad esempio, la figura mostra che la funzione f(x) assume il valore più piccolo in due punti x2 E X 2 ".

Commento. L'enunciato del teorema può diventare errato se consideriamo il valore della funzione sull'intervallo ( UN, B). Infatti, se consideriamo la funzione y = x su (0, 2), allora è continua su questo intervallo, ma non raggiunge né i valori più grandi né quelli più piccoli in esso: raggiunge questi valori alle estremità dell'intervallo, ma le estremità non appartengono al nostro dominio.

Inoltre, il teorema cessa di essere vero per le funzioni discontinue. Dare un esempio.

Conseguenza. Se la funzione f(x)è continuo su [ UN, B], allora è limitato a questo segmento.

Teorema 2. Lasciamo la funzione y = f(x)è continua nell'intervallo [ UN, B] e agli estremi di questo segmento assume valori di segno diverso, allora all'interno del segmento è presente almeno un punto x = C, in cui la funzione va a zero: f(C)= 0, dove a< C< b

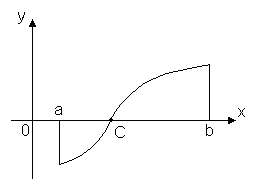
Questo teorema ha un significato geometrico semplice: se i punti del grafico di una funzione continua y = f(x), corrispondente alle estremità del segmento [ UN, B] giacciono su lati opposti dell'asse Bue, allora questo grafico interseca l'asse in almeno un punto del segmento Bue. Le funzioni discontinue potrebbero non avere questa proprietà.

Questo teorema ammette la seguente generalizzazione.

Teorema 3 (teorema del valore intermedio). Lasciamo la funzione y = f(x)è continua nell'intervallo [ UN, B] E f(a) = A, f(b) = B. Quindi per qualsiasi numero C, concluso tra UN E B, c'è un punto del genere all'interno di questo segmento CÎ [ UN, B], Che cosa f(c) = C.

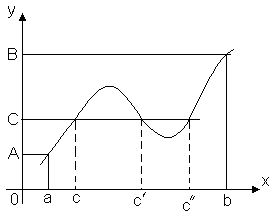
Questo teorema è geometricamente ovvio. Consideriamo il grafico della funzione y = f(x). Permettere f(a) = A, f(b) = B. Quindi qualsiasi linea retta y = C, Dove C– qualsiasi numero compreso tra UN E B, intersecherà il grafico della funzione almeno in un punto. L'ascissa del punto di intersezione sarà quel valore x = C, al quale f(c) = C.

Pertanto, una funzione continua, passando da un valore all'altro, passa necessariamente attraverso tutti i valori intermedi. In particolare:

Conseguenza. Se la funzione y = f(x)è continua su un certo intervallo e assume il valore più grande e quello più piccolo, quindi su questo intervallo assume almeno una volta qualsiasi valore compreso tra il suo valore più piccolo e quello più grande.

IL DERIVATO E LE SUE APPLICAZIONI. DEFINIZIONE DI DERIVATO

Cerchiamo di avere qualche funzione y=f(x), definito su un certo intervallo. Per ogni valore dell'argomento X da questo intervallo la funzione y=f(x) ha un certo significato.

Considera due valori di argomento: iniziale X 0 e nuovo X.

Differenza x–x 0 viene chiamato incrementando l'argomento x al punto X 0 ed è indicato Δx. Così, ∆x = x – x 0 (l'incremento dell'argomento può essere positivo o negativo). Da questa uguaglianza ne consegue che x=x 0 +Δx, cioè. il valore iniziale della variabile ha ricevuto qualche incremento. Quindi, se al punto X 0 il valore della funzione era f(x 0 ), poi in un nuovo punto X la funzione assumerà il valore f(x) = f(x 0 +Δx).

Differenza sì sì 0 = f(x) – f(x 0 ) chiamato incremento della funzione y = f(x) al punto X 0 ed è indicato dal simbolo Δy. Così,

In genere il valore iniziale dell'argomento X 0 è considerato fisso e il nuovo valore X– variabile. Poi sì 0 =f(x 0 ) risulta essere costante e y = f(x)– variabile. Incrementi Δy E Δx saranno anche variabili e la formula (1) lo mostra Dyè una funzione di una variabile Δx.

Creiamo il rapporto tra l'incremento della funzione e l'incremento dell'argomento

Troviamo il limite di questo rapporto a Δx→0. Se questo limite esiste, allora si chiama derivata di questa funzione f(x) al punto X 0 e denotare F "(X 0). COSÌ,

Derivato questa funzione y = f(x) al punto X 0 è chiamato limite del rapporto di incremento della funzione Δ sì all'argomento incremento Δ X, quando quest'ultimo tende arbitrariamente a zero.

Si noti che per la stessa funzione la derivata in punti diversi X può assumere valori diversi, ad es. la derivata può essere considerata una funzione dell'argomento X. Questa funzione è designata F "(X)

La derivata è indicata dai simboli F "(x),y", . Il valore specifico del derivato a x = a denotato da F "(UN) O sì "| x=a.

L'operazione di trovare la derivata di una funzione f(x) si chiama differenziazione di questa funzione.

Per trovare direttamente la derivata per definizione, è possibile utilizzare quanto segue: regola del pollice:

Esempi.

SENSO MECCANICO DELLA DERIVATA

È noto dalla fisica che la legge del moto uniforme ha la forma s = vt, Dove S– il percorso percorso fino al momento del tempo T, v– velocità del moto uniforme.

Tuttavia, perché La maggior parte dei movimenti che si verificano in natura sono irregolari, quindi in generale la velocità e, di conseguenza, la distanza S dipenderà dal tempo T, cioè. sarà una funzione del tempo.

Quindi, lasciamo che un punto materiale si muova in linea retta in una direzione secondo la legge s=s(t).

Segniamo un certo punto nel tempo T 0 . A questo punto il punto ha superato il sentiero s=s(t 0 ). Determiniamo la velocità v punto materiale in un dato momento T 0 .

Per fare ciò, consideriamo qualche altro momento T 0 + Δ T. Corrisponde al percorso percorso s =s(t 0 + Δ T). Quindi in un periodo di tempo Δ T il punto ha percorso il percorso Δs =s(t 0 + Δ T)–s(t).

Consideriamo l'atteggiamento. Si chiama velocità media nell'intervallo di tempo Δ T. La velocità media al momento non può caratterizzare con precisione la velocità di movimento di un punto T 0 (perché il movimento non è uniforme). Per esprimere in modo più accurato questa velocità reale utilizzando la velocità media, è necessario prendere un periodo di tempo più breve Δ T.

Quindi, la velocità del movimento in un dato momento nel tempo T 0 (velocità istantanea) è il limite della velocità media nell'intervallo da T 0 a T 0 +Δ T, quando Δ T→0:

,

quelli. velocità irregolare questa è la derivata della distanza percorsa rispetto al tempo.

SIGNIFICATO GEOMETRICO DEL DERIVATO

Introduciamo innanzitutto la definizione di tangente ad una curva in un dato punto.

Prendiamo una curva e un punto fisso su di essa M0(vedi figura) Consideriamo un altro punto M questa curva e disegna una secante M0M. Se il punto M inizia a muoversi lungo la curva e il punto M0 rimane immobile, poi la secante cambia posizione. Se, con approssimazione illimitata del punto M lungo una curva fino ad un punto M0 da ogni lato la secante tende ad occupare la posizione di una certa retta M0T, poi dritto M0T chiamata tangente alla curva in un dato punto M0.

Quello., tangente alla curva in un dato punto M0 detta posizione limite della secante M0M quando punto M tende lungo la curva fino ad un punto M0.

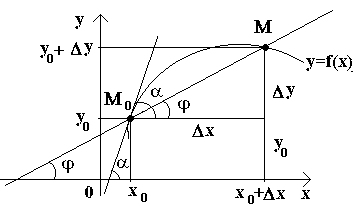
Consideriamo ora la funzione continua y=f(x) e la curva corrispondente a questa funzione. Ad un certo valore X 0 la funzione assume valore y0 =f(x0). Questi valori X 0 e sì 0 sulla curva corrisponde ad un punto M0 (x0; y0). Diamo l'argomentazione x0 incremento Δ X. Il nuovo valore dell'argomento corrisponde al valore incrementato della funzione sì 0 +Δ y=f(x 0 –Δ X). Abbiamo capito il punto M(x0+Δ X; e 0+Δ sì). Disegniamo una secante M0M e indichiamo con φ l'angolo formato da una secante con la direzione positiva dell'asse Bue. Creiamo una relazione e notiamolo.

Se ora Δ X→0, quindi per la continuità della funzione Δ A→0, e quindi il punto M, muovendosi lungo una curva, si avvicina al punto senza limiti M0. Quindi la secante M0M tenderà ad assumere la posizione di tangente alla curva in quel punto M0 e l'angolo φ→α in Δ X→0, dove α indica l'angolo tra la tangente e la direzione positiva dell'asse Bue. Poiché la funzione tan φ dipende continuamente da φ per φ≠π/2, allora per φ→α tan φ → tan α e, quindi, la pendenza della tangente sarà:

quelli. f"(x)= tgα .

Così, geometricamente y"(x0) rappresenta la pendenza della tangente al grafico di questa funzione nel punto x0, cioè. per un dato valore di argomento X, la derivata è uguale alla tangente dell'angolo formato dalla tangente al grafico della funzione f(x) al punto opportuno M0 (x; y) con direzione dell'asse positiva Bue.

Esempio. Trova la pendenza della tangente alla curva y = x 2 al punto M(-1; 1).

Abbiamo già visto in precedenza che ( X 2)" = 2X. Ma il coefficiente angolare della tangente alla curva è tan α = sì"|x=-1 = –2.

DIFFERENZIABILITÀ DELLE FUNZIONI. CONTINUITÀ DELLA FUNZIONE DIFFERENZIABILE

Funzione y=f(x) chiamato differenziabile ad un certo punto X 0 se a questo punto ha una certa derivata, cioè se il limite della relazione esiste ed è finito.

Se una funzione è differenziabile in ogni punto di un certo segmento [ UN; B] o intervallo ( UN; B), poi dicono che lei differenziabile sul segmento [ UN; B] o, rispettivamente, nell'intervallo ( UN; B).

Vale il seguente teorema che stabilisce la connessione tra funzioni differenziabili e continue.

Teorema. Se la funzione y=f(x) differenziabile ad un certo punto x0, allora a questo punto è continua.

Dalla differenziabilità di una funzione consegue quindi la sua continuità.

Prova. Se , Quello

,

dove α è una quantità infinitesima, cioè una quantità tendente a zero come Δ X→0. Ma allora

Δ sì=F "(x0) Δ X+αΔ X=> Δ sì→0 a Δ X→0, cioè f(x) – f(x 0)→0 a X→X 0 , il che significa che la funzione f(x) continuo in un punto X 0 . Q.E.D.

Pertanto, la funzione non può avere una derivata nei punti di discontinuità. Non è vero il contrario: ci sono funzioni continue che non sono differenziabili in alcuni punti (cioè non hanno derivata in questi punti).

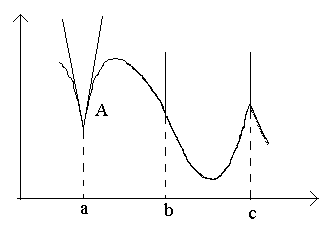
Considera i punti nella figura a, b, c.

Al punto UN a Δ X→0 il rapporto non ha limiti (poiché i limiti unilaterali sono diversi per Δ X→0–0 e Δ X→0+0). Al punto UN Nel grafico non esiste una tangente definita, ma esistono due diverse tangenti unidirezionali con pendenze A 1 e A 2. Questo tipo di punto è chiamato punto d'angolo.

Al punto B a Δ X Il rapporto →0 è un segno costante di quantità infinitamente grande. La funzione ha derivata infinita. A questo punto il grafico ha una tangente verticale. Tipo di punto – “punto di flesso” di una tangente verticale.

Al punto C le derivate unilaterali sono quantità infinitamente grandi di segni diversi. A questo punto il grafico ha due tangenti verticali unite. Tipo – “punto di ritorno” con una tangente verticale – un caso speciale di punto d'angolo.

Le figure seguenti mostrano dove la funzione può raggiungere il suo valore più piccolo e quello più grande. Nella figura a sinistra, i valori più piccolo e più grande sono fissati nei punti di minimo e massimo locale della funzione. Nella foto a destra - alle estremità del segmento.

Se la funzione sì = F(X) è continua nell'intervallo [ UN, B] , quindi raggiunge questo segmento meno E valori più alti . Ciò, come già accennato, può avvenire sia in punti estremi o alle estremità del segmento. Pertanto, per trovare meno E i valori più grandi della funzione , continuo sull'intervallo [ UN, B] , è necessario calcolarne i valori in tutto punti critici e alle estremità del segmento, quindi scegli tra essi il più piccolo e il più grande.

Supponiamo, ad esempio, di voler determinare il valore più grande della funzione F(X) sul segmento [ UN, B] . Per fare questo, devi trovare tutti i suoi punti critici che giacciono su [ UN, B] .

Punto critico chiamato il punto in cui funzione definita, e lei derivato o uguale a zero o non esiste. Quindi dovresti calcolare i valori della funzione nei punti critici. E infine, si dovrebbero confrontare i valori della funzione nei punti critici e alle estremità del segmento ( F(UN) E F(B)). Il più grande di questi numeri sarà il valore più grande della funzione sul segmento [UN, B] .

Problemi di reperimento valori di funzione più piccoli .

Cerchiamo insieme i valori più piccoli e più grandi della funzione

Esempio 1. Trova i valori più piccoli e più grandi di una funzione sul segmento [-1, 2] .

Soluzione. Trova la derivata di questa funzione. Uguagliamo la derivata a zero () e otteniamo due punti critici: e . Per trovare i valori più piccoli e più grandi di una funzione su un dato segmento, è sufficiente calcolarne i valori alle estremità del segmento e nel punto, poiché il punto non appartiene al segmento [-1, 2]. Questi valori di funzione sono: , , . Ne consegue che valore della funzione più piccolo(indicato in rosso nel grafico sottostante), pari a -7, si ottiene all'estremità destra del segmento - nel punto , e più grande(anche rosso nel grafico), equivale a 9, - nel punto critico.

Se una funzione è continua in un certo intervallo e questo intervallo non è un segmento (ma è, ad esempio, un intervallo; la differenza tra un intervallo e un segmento: i punti di confine dell'intervallo non sono compresi nell'intervallo, ma i i punti di confine del segmento sono inclusi nel segmento), allora tra i valori della funzione potrebbe non esserci quello più piccolo e quello più grande. Quindi, ad esempio, la funzione mostrata nella figura sotto è continua su ]-∞, +∞[ e non ha il valore massimo.

Tuttavia, per qualsiasi intervallo (chiuso, aperto o infinito), vale la seguente proprietà delle funzioni continue.

Per l'autocontrollo durante i calcoli, è possibile utilizzare calcolatore di derivati ​​online .

Esempio 4. Trova i valori più piccoli e più grandi di una funzione sul segmento [-1, 3] .

Soluzione. Troviamo la derivata di questa funzione come derivata del quoziente:

.

Identifichiamo la derivata a zero, il che ci fornisce un punto critico: . Appartiene al segmento [-1, 3] . Per trovare i valori più piccoli e più grandi di una funzione su un dato segmento, troviamo i suoi valori alle estremità del segmento e nel punto critico trovato:

Confrontiamo questi valori. Conclusione: pari a -5/13, al punto e valore più alto uguale a 1 al punto .

Continuiamo a cercare insieme i valori più piccoli e più grandi della funzione

Ci sono insegnanti che, riguardo alla ricerca dei valori più piccoli e più grandi di una funzione, non danno agli studenti esempi da risolvere più complessi di quelli appena discussi, cioè quelli in cui la funzione è un polinomio o un frazione, il cui numeratore e denominatore sono polinomi. Ma non ci limiteremo a tali esempi, poiché tra gli insegnanti ci sono quelli a cui piace costringere gli studenti a pensare per intero (la tabella delle derivate). Verranno quindi utilizzati il ​​logaritmo e la funzione trigonometrica.

Esempio 8. Trova i valori più piccoli e più grandi di una funzione sul segmento .

Soluzione. Troviamo la derivata di questa funzione come derivato del prodotto :

Uguagliamo la derivata a zero, il che fornisce un punto critico: . Appartiene al segmento. Per trovare i valori più piccoli e più grandi di una funzione su un dato segmento, troviamo i suoi valori alle estremità del segmento e nel punto critico trovato:

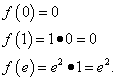
Risultato di tutte le azioni: la funzione raggiunge il suo valore minimo, uguale a 0, al punto e al punto e valore più alto, uguale e², al punto.

Per l'autocontrollo durante i calcoli, è possibile utilizzare calcolatore di derivati ​​online .

Esempio 9. Trova i valori più piccoli e più grandi di una funzione sul segmento .

Soluzione. Trova la derivata di questa funzione:

Uguagliamo la derivata a zero:

L'unico punto critico appartiene al segmento. Per trovare i valori più piccoli e più grandi di una funzione su un dato segmento, troviamo i suoi valori alle estremità del segmento e nel punto critico trovato:

Conclusione: la funzione raggiunge il suo valore minimo, uguale a , nel punto e valore più alto, uguale , al punto .

Nei problemi estremi applicati, trovare i valori più piccoli (massimi) di una funzione, di regola, si riduce a trovare il minimo (massimo). Ma non sono i minimi o i massimi in sé ad essere di maggiore interesse pratico, ma quei valori dell’argomentazione con cui vengono raggiunti. Quando si risolvono problemi applicati, sorge un'ulteriore difficoltà: comporre funzioni che descrivono il fenomeno o il processo in esame.

Esempio 10. Deve essere stagnata una vasca della capacità di 4 persone, avente forma di parallelepipedo a base quadrata e aperta superiormente. Che dimensioni dovrebbe avere il serbatoio in modo che venga utilizzata la minor quantità di materiale per coprirlo?

Soluzione. Permettere X- lato base, H- altezza del serbatoio, S- la sua superficie senza copertura, V- il suo volume. La superficie del serbatoio è espressa dalla formula, cioè è una funzione di due variabili. Esprimere S come funzione di una variabile, usiamo il fatto che , da dove . Sostituendo l'espressione trovata H nella formula per S:

Esaminiamo questa funzione fino al suo estremo. È definito e differenziabile ovunque in ]0, +∞[ , e

.

Uguagliamo la derivata a zero () e troviamo il punto critico. Inoltre, quando la derivata non esiste, ma questo valore non è compreso nel dominio di definizione e quindi non può essere un punto estremo. Quindi questo è l’unico punto critico. Controlliamo la presenza di un estremo utilizzando il secondo segno sufficiente. Troviamo la derivata seconda. Quando la derivata seconda è maggiore di zero (). Ciò significa che quando la funzione raggiunge il minimo . Da questo minimo è l'unico estremo di questa funzione, è il suo valore più piccolo. Quindi, il lato della base del serbatoio dovrebbe essere di 2 me la sua altezza dovrebbe essere di .

Per l'autocontrollo durante i calcoli, è possibile utilizzare

Da un punto di vista pratico, l'interesse maggiore è utilizzare la derivata per trovare i valori più grandi e più piccoli di una funzione. A cosa è collegato questo? Massimizzare i profitti, minimizzare i costi, determinare il carico ottimale delle attrezzature... In altre parole, in molti ambiti della vita dobbiamo risolvere problemi di ottimizzazione di alcuni parametri. E questi sono i compiti di trovare i valori più grandi e più piccoli di una funzione.

Va notato che i valori più grandi e più piccoli di una funzione vengono solitamente ricercati su un certo intervallo X, che è l'intero dominio della funzione o parte del dominio di definizione. L'intervallo X stesso può essere un segmento, un intervallo aperto , un intervallo infinito.

In questo articolo parleremo di come trovare i valori più grandi e più piccoli di una funzione definita esplicitamente di una variabile y=f(x) .

Navigazione della pagina.

Il valore più grande e più piccolo di una funzione: definizioni, illustrazioni.

Vediamo brevemente le principali definizioni.

Il valore più grande della funzione quello per chiunque la disuguaglianza è vera.

Il valore più piccolo della funzione y=f(x) sull'intervallo X è chiamato tale valore quello per chiunque la disuguaglianza è vera.

Queste definizioni sono intuitive: il valore più grande (più piccolo) di una funzione è il valore più grande (più piccolo) accettato sull'intervallo considerato nell'ascissa.

Punti stazionari– questi sono i valori dell’argomento ai quali la derivata della funzione diventa zero.

Perché abbiamo bisogno di punti stazionari quando troviamo i valori più grandi e più piccoli? La risposta a questa domanda è data dal teorema di Fermat. Da questo teorema segue che se una funzione differenziabile ha un estremo (minimo locale o massimo locale) in un punto, allora questo punto è stazionario. Pertanto, la funzione spesso assume il suo valore più grande (più piccolo) sull'intervallo X in uno dei punti stazionari di questo intervallo.

Inoltre, una funzione può spesso assumere i suoi valori più grandi e più piccoli nei punti in cui la derivata prima di questa funzione non esiste e la funzione stessa è definita.

Rispondiamo subito a una delle domande più comuni su questo argomento: “È sempre possibile determinare il valore più grande (più piccolo) di una funzione”? No, non sempre. A volte i confini dell'intervallo X coincidono con i confini del dominio di definizione della funzione, oppure l'intervallo X è infinito. E alcune funzioni all'infinito e ai confini del dominio di definizione possono assumere valori sia infinitamente grandi che infinitamente piccoli. In questi casi non si può dire nulla sul valore più grande e su quello più piccolo della funzione.

Per chiarezza forniremo un'illustrazione grafica. Guarda le immagini e tutto ti sarà più chiaro.

Sul segmento

Nella prima figura, la funzione assume i valori più grande (max y) e più piccolo (min y) nei punti stazionari situati all'interno del segmento [-6;6].

Consideriamo il caso rappresentato nella seconda figura. Cambiamo il segmento in . In questo esempio, il valore più piccolo della funzione si ottiene in un punto stazionario e il più grande nel punto in cui l'ascissa corrisponde al limite destro dell'intervallo.

Nella Figura 3, i punti di confine del segmento [-3;2] sono le ascisse dei punti corrispondenti al valore più grande e più piccolo della funzione.

Su un intervallo aperto

Nella quarta figura, la funzione assume i valori più grande (max y) e più piccolo (min y) nei punti stazionari situati all'interno dell'intervallo aperto (-6;6).

Nell'intervallo non è possibile trarre conclusioni sul valore più grande.

All'infinito

Nell'esempio presentato nella settima figura, la funzione assume il valore più grande (max y) in un punto stazionario con ascissa x=1, e il valore più piccolo (min y) viene raggiunto sul limite destro dell'intervallo. A meno infinito, i valori della funzione si avvicinano asintoticamente a y=3.

Nell'intervallo la funzione non raggiunge né il valore più piccolo né quello più grande. Quando x=2 si avvicina da destra, i valori della funzione tendono a meno infinito (la linea x=2 è un asintoto verticale), e quando l'ascissa tende a più infinito, i valori della funzione si avvicinano asintoticamente a y=3. Un'illustrazione grafica di questo esempio è mostrata nella Figura 8.

Algoritmo per trovare i valori più grandi e più piccoli di una funzione continua su un segmento.

Scriviamo un algoritmo che ci permetta di trovare i valori più grandi e più piccoli di una funzione su un segmento.

1. Troviamo il dominio di definizione della funzione e controlliamo se contiene l'intero segmento.
2. Troviamo tutti i punti in cui non esiste la derivata prima e che sono contenuti nel segmento (solitamente tali punti si trovano nelle funzioni con argomento sotto il segno modulo e nelle funzioni potenza con esponente frazionario-razionale). Se non ci sono tali punti, passa al punto successivo.
3. Determiniamo tutti i punti stazionari che rientrano nel segmento. Per fare ciò, lo equiparamo a zero, risolviamo l'equazione risultante e selezioniamo le radici adatte. Se non ci sono punti stazionari o nessuno di essi rientra nel segmento, passa al punto successivo.
4. Calcoliamo i valori della funzione nei punti stazionari selezionati (se presenti), nei punti in cui la derivata prima non esiste (se presente), nonché in x=a e x=b.
5. Dai valori ottenuti della funzione, selezioniamo il più grande e il più piccolo: saranno rispettivamente i valori più grande e più piccolo richiesti della funzione.

Analizziamo l'algoritmo per risolvere un esempio per trovare i valori più grandi e più piccoli di una funzione su un segmento.

Esempio.

Trovare il valore più grande e più piccolo di una funzione

• sul segmento;
• sul segmento [-4;-1] .

Soluzione.

Il dominio di definizione di una funzione è l'intero insieme dei numeri reali, ad eccezione dello zero. Entrambi i segmenti rientrano nel dominio di definizione.

Trovare la derivata della funzione rispetto a:

Ovviamente la derivata della funzione esiste in tutti i punti dei segmenti e [-4;-1].

Determiniamo i punti stazionari dall'equazione. L'unica radice reale è x=2. Questo punto stazionario rientra nel primo segmento.

Per il primo caso calcoliamo i valori della funzione agli estremi del segmento e nel punto stazionario, cioè per x=1, x=2 e x=4:

Pertanto, il valore massimo della funzione si ottiene con x=1 e il valore più piccolo – in x=2.

Per il secondo caso calcoliamo i valori della funzione solo agli estremi del segmento [-4;-1] (poiché non contiene un solo punto stazionario):

Soluzione.

Cominciamo con il dominio della funzione. Il trinomio quadrato al denominatore della frazione non deve svanire:

È facile verificare che tutti gli intervalli dell'enunciazione del problema appartengono al dominio di definizione della funzione.

Differenziamo la funzione:

Ovviamente la derivata esiste in tutto il dominio di definizione della funzione.

Troviamo i punti stazionari. La derivata va a zero in . Questo punto stazionario rientra negli intervalli (-3;1] e (-3;2).

Ora puoi confrontare i risultati ottenuti in ogni punto con il grafico della funzione. Le linee tratteggiate blu indicano gli asintoti.

A questo punto possiamo concludere trovando i valori più grandi e più piccoli della funzione. Gli algoritmi discussi in questo articolo ti consentono di ottenere risultati con un minimo di azioni. Tuttavia, può essere utile determinare prima gli intervalli di aumento e diminuzione della funzione e solo dopo trarre conclusioni sui valori più grandi e più piccoli della funzione su qualsiasi intervallo. Ciò fornisce un quadro più chiaro e una giustificazione rigorosa dei risultati.

Definizione3 . 3 Sia una funzione, il suo dominio di definizione e un intervallo (aperto) (magari con e/o ) 7 . Chiamiamo la funzione continuo nell'intervallo, se continua in ogni punto, cioè per qualunque cosa esista (in forma abbreviata:

Sia ora un segmento (chiuso) in . Chiamiamo la funzione continuo sul segmento, se continuo sull'intervallo, continuo a destra nel punto e continuo a sinistra nel punto, cioè

Esempio3 . 13 Considera la funzione (Funzione Heaviside) sul segmento , . Allora è continua sul segmento (malgrado abbia in quel punto una discontinuità del primo tipo).

Fig. 3.15 Grafico della funzione Heaviside

Una definizione simile può essere data per i semiintervalli della forma e , compresi i casi e . Tuttavia, possiamo generalizzare questa definizione al caso di un sottoinsieme arbitrario come segue. Introduciamo innanzitutto il concetto indotto alle basi: sia una base le cui terminazioni abbiano tutte intersezioni non vuote con . Indichiamo con e consideriamo l'insieme di tutti . È quindi facile verificare che il set sarà la base. Pertanto, per le basi , e , dove , e sono le basi di quartieri non perforati a due lati (rispettivamente sinistro, destro) di un punto (vedere la loro definizione all'inizio del presente capitolo).

Definizione3 . 4 Chiamiamo la funzione continuo sul set, Se

È facile vedere che allora at e at questa definizione coincide con quelle date sopra specificatamente per intervallo e segmento.

Ricordiamo che tutte le funzioni elementari sono continue in tutti i punti dei loro domini di definizione e, quindi, continue su qualsiasi intervallo e segmento che giace nei loro domini di definizione.

Poiché la continuità su un intervallo e segmento è definita puntualmente, vale il teorema, che è una conseguenza immediata del Teorema 3.1:

Teorema3 . 5 Permettere E -- funzioni e - intervallo o segmento situato all'interno . Permettere E continuo per . Poi le funzioni , , continuo per . Se in aggiunta davanti a tutti , quindi la funzione è anche continuo .

Da questo teorema, così come dal Teorema 3.1 - Proposizione 3.3, segue la seguente affermazione:

Offerta3 . 4 Un mucchio di tutte le funzioni continuano su un intervallo o segmento -- questo è uno spazio lineare:

Una proprietà più complessa di una funzione continua è espressa dal seguente teorema.

Teorema3 . 6 (sulla radice di una funzione continua) Lasciamo la funzione continuo sul segmento , E E -- Numeri di segni diversi. (Per certezza, lo assumeremo , UN .) Allora esiste almeno uno di questi valori , Che cosa (ovvero, esiste almeno una radice equazioni ).

Prova. Diamo un'occhiata al centro del segmento. Allora è o, o, o. Nel primo caso si trova la radice: questa è . Nei restanti due casi si consideri quella parte del segmento agli estremi della quale la funzione assume valori di segno diverso: in case o in case . Denotiamo la metà selezionata del segmento con e applichiamo ad essa la stessa procedura: dividiamola in due metà e , dove , e trova . Nel caso in cui venga trovata la radice; nel caso consideriamo ulteriormente il segmento , in caso - segmento eccetera.

Fig. 3.16 Divisioni consecutive di un segmento a metà

Otteniamo che ad un certo punto verrà trovata la radice o verrà costruito un sistema di segmenti annidati

in cui ogni segmento successivo è lungo la metà del precedente. La sequenza è non decrescente e delimitata dall'alto (ad esempio dal numero); quindi (per il Teorema 2.13), ha un limite. Sotto sequenza - non crescente e delimitato inferiormente (ad esempio dal numero ); questo significa che c'è un limite. Poiché le lunghezze dei segmenti formano una progressione geometrica decrescente (con denominatore ), tendono a 0, e , questo è . Mettiamolo adesso. Poi

E

poiché la funzione è continua. Tuttavia, costruendo le successioni e , e , in modo che, per il teorema del passaggio al limite nella disuguaglianza (Teorema 2.7), e , cioè, e . Ciò significa che , ed è la radice dell'equazione.

Esempio3 . 14 Considera la funzione sul segmento. Poiché e sono numeri con segni diversi, la funzione passa a 0 ad un certo punto dell'intervallo. Ciò significa che l'equazione ha una radice.

Fig. 3.17 Rappresentazione grafica della radice dell'equazione

Il teorema dimostrato in realtà ci dà un modo per trovare la radice, almeno approssimativa, con qualsiasi grado di precisione specificato in anticipo. Questo è il metodo per dividere un segmento a metà, descritto nella dimostrazione del teorema. Faremo conoscenza con questo e altri metodi più efficaci per trovare approssimativamente la radice in modo più dettagliato di seguito, dopo aver studiato il concetto e le proprietà di un derivato.

Si noti che il teorema non afferma che se le sue condizioni sono soddisfatte, la radice è unica. Come mostra la figura seguente, può esserci più di una radice (ce ne sono 3 nella figura).

Fig. 3.18 Diverse radici di una funzione che assume valori di segni diversi alle estremità del segmento

Tuttavia, se una funzione aumenta o diminuisce monotonicamente su un segmento, alle estremità del quale assume valori di segni diversi, allora la radice è unica, poiché una funzione strettamente monotona assume ciascuno dei suoi valori esattamente in un punto , compreso il valore 0.

Fig. 3.19 Una funzione monotona non può avere più di una radice

Una conseguenza immediata del teorema sulla radice di una funzione continua è il seguente teorema, che di per sé è molto importante nell'analisi matematica.

Teorema3 . 7 (circa il valore intermedio di una funzione continua) Lasciamo la funzione continuo sul segmento E (per certezza lo assumeremo ). Permettere - qualche numero che si trova nel mezzo E . Allora c'è un punto del genere , Che cosa .

Fig. 3.20 La funzione continua assume qualsiasi valore intermedio

Prova. Considera la funzione di aiuto , Dove . Poi E . La funzione è ovviamente continua, e per il teorema precedente esiste un punto tale che . Ma questa uguaglianza significa che.

Tieni presente che se la funzione non è continua, potrebbe non assumere tutti i valori intermedi. Ad esempio, la funzione Heaviside (vedi Esempio 3.13) accetta i valori , , ma da nessuna parte, incluso nell'intervallo, assume, ad esempio, un valore intermedio. Il fatto è che la funzione Heaviside ha una discontinuità in un punto che si trova esattamente nell'intervallo.

Per studiare ulteriormente le proprietà delle funzioni continue su un intervallo, avremo bisogno della seguente sottile proprietà del sistema dei numeri reali (ne abbiamo già parlato nel Capitolo 2 a proposito del teorema sul limite di una funzione limitata monotonicamente crescente): per qualsiasi insieme limitato inferiormente (cioè tale che per tutti e alcuni; il numero si chiama bordo inferiore set) disponibili bordo inferiore esatto, cioè il più grande dei numeri tale che per tutti . Allo stesso modo, se un insieme è limitato superiormente, allora lo è limite superiore esatto: questo è il più piccolo dei facce superiori(per cui per tutti).

Fig. 3.21 Limiti inferiore e superiore di un insieme limitato

Se , allora esiste una sequenza non crescente di punti che tende a . Allo stesso modo, se , allora esiste una sequenza non decrescente di punti che tende a .

Se un punto appartiene all'insieme, allora è l'elemento più piccolo di questo insieme: ; allo stesso modo se , Quello .

Inoltre, per ulteriore avremo bisogno di quanto segue

Lemma3 . 1 Permettere -- funzione continua su un segmento , e molti quei punti , in quale (O , O ) non è vuoto. Poi in abbondanza c'è un valore più piccolo , tale che davanti a tutti .

Fig. 3.22 L'argomento più piccolo in corrispondenza del quale la funzione assume il valore specificato

Prova. Poiché è un insieme limitato (fa parte di un segmento), ha un minimo. Allora esiste una successione non crescente , , tale che per . Inoltre, per la definizione di insieme. Pertanto, passando al limite, otteniamo, da un lato,

e d’altro canto, per la continuità della funzione,

Ciò significa che , quindi il punto appartiene all'insieme e .

Nel caso in cui l'insieme sia definito dalla disuguaglianza, abbiamo per tutti e per il teorema sul passaggio al limite nella disuguaglianza otteniamo

da dove , il che significa che e . Allo stesso modo, nel caso della disuguaglianza, il passaggio al limite della disuguaglianza dà

da dove , e .

Teorema3 . 8 (sulla limitatezza di una funzione continua) Lasciamo la funzione continuo sul segmento . Poi limitato a , cioè esiste una tale costante , Che cosa davanti a tutti .

Fig. 3.23 Una funzione continua su un segmento è limitata

Prova. Supponiamo il contrario: non sia limitato, ad esempio, dall'alto. Quindi tutti gli insiemi , , , non sono vuoti. Per il lemma precedente, ciascuno di questi insiemi ha il valore più piccolo , . Mostriamolo

Veramente, . Se un punto qualsiasi da , ad esempio, si trova tra e , allora

cioè un valore intermedio tra e . Ciò significa che, per il teorema sul valore intermedio di una funzione continua, esiste un punto tale che , E . Ma, contrariamente al presupposto, il valore più piccolo dell'insieme. Ne consegue che per tutti.

Allo stesso modo, è ulteriormente dimostrato che for all , for all , ecc. Quindi, è una sequenza crescente delimitata superiormente dal numero . Quindi esiste. Dalla continuità della funzione consegue che c'è , Ma a , quindi non c'è limite. La contraddizione risultante dimostra che la funzione è limitata superiormente.

In modo analogo si dimostra che è delimitato dal basso, il che implica l'enunciazione del teorema.

Ovviamente non è possibile indebolire le condizioni del teorema: se una funzione non è continua, allora non deve essere limitata su un intervallo (diamo come esempio la funzione

sul segmento. Questa funzione non è limitata all'intervallo, poiché ha un punto di discontinuità del secondo tipo, tale che A . È anche impossibile sostituire un segmento nella condizione del teorema con un intervallo o semiintervallo: consideriamo ad esempio la stessa funzione su un semiintervallo. La funzione è continua su questo semiintervallo, ma illimitata, poiché in .

Trovare le migliori costanti che possono essere utilizzate per limitare una funzione dall'alto e dal basso su un dato intervallo ci porta naturalmente al problema di trovare il minimo e il massimo di una funzione continua su questo intervallo. La possibilità di risolvere questo problema è descritta dal seguente teorema.

Teorema3 . 9 (sul raggiungimento di un estremo da parte di una funzione continua) Lasciamo la funzione continuo sul segmento . Allora c'è un punto , tale che davanti a tutti (questo è -- punto minimo: ), e c'è un punto , tale che davanti a tutti (questo è -- punto massimo: ). In altre parole, il minimo e il massimo 8 i valori di una funzione continua su un segmento esistono e vengono raggiunti in alcuni punti E questo segmento.

Fig. 3.24 Una funzione continua su un segmento raggiunge un massimo e un minimo

Prova. Poiché, secondo il teorema precedente, la funzione è limitata da sopra, esiste un limite superiore esatto per i valori della funzione da --numero . Pertanto, gli insiemi , ,..., ,..., non sono vuoti e, per il lemma precedente, contengono i valori più piccoli: , . Questi non diminuiscono (questa affermazione si dimostra esattamente nello stesso modo del teorema precedente):

e sono limitati dall'alto da . Pertanto, secondo il teorema sul limite di una successione limitata monotona, esiste un limite Poiché , Poi

dal teorema del passaggio al limite di disuguaglianza, cioè . Ma con tutti, compreso. Da ciò risulta che cioè il massimo della funzione si ottiene nel punto .

L’esistenza di un punto di minimo si dimostra in modo analogo.

In questo teorema, come nel precedente, non è possibile indebolire le condizioni: se la funzione non è continua, allora potrebbe non raggiungere il suo valore massimo o minimo sul segmento, anche se è limitato. Prendiamo ad esempio la funzione

sul segmento. Questa funzione è limitata all'intervallo (ovviamente) e , tuttavia, non assume il valore 1 in nessun punto del segmento (nota che , non 1). Il fatto è che questa funzione ha una discontinuità del primo tipo nel punto , per cui al limite non è uguale al valore della funzione nel punto 0. Inoltre, una funzione continua definita su un intervallo o altro insieme che non è un segmento chiuso (su semiintervallo, semiasse) può anche non assumere valori estremi. Ad esempio, considera una funzione sull'intervallo . È ovvio che la funzione è continua e che, tuttavia, la funzione non assume né il valore 0 né il valore 1 in nessun punto dell'intervallo . Consideriamo anche la funzione sul semiasse. Questa funzione è continua su , aumenta, assume il suo valore minimo 0 nel punto , ma non assume un valore massimo in nessun punto (sebbene sia limitata dall'alto dal numero e

Definizione. Se la funzione F(X) è definito sull'intervallo [ un, b], è continua in ogni punto dell'intervallo ( un, b), al punto UN continuo a destra, nel punto Bè continua a sinistra, allora diciamo che la funzione F(X) continuo sul segmento [un, b].

In altre parole, la funzione F(X) è continua sull'intervallo [ un, b], se sono soddisfatte tre condizioni:

1) "X 0 Î( un, b): F(X) = F(X 0);

2) F(X) = F(UN);

3) F(X) = F(B).

Per funzioni continue su un intervallo consideriamo alcune proprietà, che formuliamo sotto forma dei seguenti teoremi, senza effettuare dimostrazioni.

Teorema 1. Se la funzione F(X) è continua sull'intervallo [ un, b], quindi raggiunge i suoi valori minimo e massimo su questo segmento.

Questo teorema afferma (Fig. 1.15) che sul segmento [ un, b] c'è un punto del genere X 1 quello F(X 1)£ F(X) per ogni X da [ un, b] e che c'è un punto X 2 (X 2 О[ un, b]) tale che " XÎ[ un, b] (F(X 2)³ F(X)).

Senso F(X 1) è il più grande per una data funzione su [ un, b], UN F(X 2) – il più piccolo. Indichiamo: F(X 1) = M, F(X 2) =M. Poiché per F(X) vale la disuguaglianza: " XÎ[ un, b] M£ F(X) £ M, allora dal Teorema 1 si ottiene il seguente corollario.

Conseguenza. Se la funzione F(X) è continua su un intervallo, allora è limitata su questo intervallo.

Teorema 2. Se la funzione F(X) è continua sull'intervallo [ un, b] e alle estremità del segmento assume valori di segni diversi, quindi esiste un tale punto interno X 0 segmento [ un, b], in cui la funzione passa a 0, cioè $ X 0 Î ( un, b) (F(X 0) = 0).

Questo teorema afferma che il grafico di una funzione y = f(X), continuo sull'intervallo [ un, b], interseca l'asse Bue almeno una volta se i valori F(UN) E F(B) hanno segni opposti. Quindi, (Fig. 1.16) F(UN) > 0, F(B) < 0 и функция F(X) diventa 0 nei punti X 1 , X 2 , X 3 .

Teorema 3. Lasciamo la funzione F(X) è continua sull'intervallo [ un, b], F(UN) = UN, F(B) = B E UN¹ B. (Fig. 1.17). Quindi per qualsiasi numero C, racchiuso tra i numeri UN E B, esiste un tale punto interiore X 0 segmento [ un, b], Che cosa F(X 0) = C.

Conseguenza. Se la funzione F(X) è continua sull'intervallo [ un, b], M– valore più piccolo F(X), M– il valore massimo della funzione F(X) sul segmento [ un, b], allora la funzione assume (almeno una volta) qualsiasi valore M, concluso tra M E M, e quindi il segmento [ mm] è l'insieme di tutti i valori della funzione F(X) sul segmento [ un, b].

Si noti che se una funzione è continua nell'intervallo ( un, b) o ha sul segmento [ un, b] punti di discontinuità, allora i Teoremi 1, 2, 3 per tale funzione cessano di essere veri.

In conclusione, consideriamo il teorema sull'esistenza di una funzione inversa.

Teorema 4. Permettere F(X) è continua nell'intervallo X, aumenta (o diminuisce) di X e ha un intervallo di valori Y. Quindi per la funzione y = f(X) esiste una funzione inversa X= J(sì), definito nell'intervallo Y, continuo e crescente (o decrescente) di Y con molteplici significati X.

Commento. Lasciamo la funzione X= J(sì) è l'inverso della funzione F(X). Poiché l'argomento è solitamente indicato con X e la funzione through sì, quindi scriviamo la funzione inversa nella forma y=J(X).

Esempio 1. Funzione y = x 2 (Fig. 1.8, a) sul set X= }