Spektrum zweier Rechteckimpulse. Spektrale Zusammensetzung einer Folge von Rechteckimpulsen mit unterschiedlichem Tastverhältnis
Literatur: [L.1], S. 40
Als Beispiel geben wir die Fourier-Reihenentwicklung einer periodischen Folge von Rechteckimpulsen mit Amplitude, Dauer und Wiederholungsperiode, symmetrisch um Null, d. h.
 , (2.10)
, (2.10)
Hier 
Die Erweiterung eines solchen Signals in eine Fourier-Reihe ergibt
 , (2.11)
, (2.11)
Wo ist der Arbeitszyklus?
Um die Notation zu vereinfachen, können Sie die Notation eingeben
 , (2.12)
, (2.12)
Dann wird (2.11) wie folgt geschrieben
 , (2.13)
, (2.13)
In Abb. 2.3 zeigt eine Folge von Rechteckimpulsen. Das Spektrum der Sequenz ist wie jedes andere periodische Signal diskreter (Linien-) Natur.
Die Spektrumhüllkurve (Abb. 2.3, b) ist proportional  . Der Abstand entlang der Frequenzachse zwischen zwei benachbarten Spektrumskomponenten beträgt , und zwischen zwei Nullwerten (die Breite der Spektrumskeule) beträgt . Die Anzahl der harmonischen Komponenten innerhalb einer Keule, einschließlich des Nullwerts rechts in der Abbildung, beträgt , wobei das Vorzeichen das Runden auf die nächste ganze Zahl bedeutet, weniger (wenn das Tastverhältnis eine Bruchzahl ist) oder (wenn das Tastverhältnis eine Bruchzahl ist). ist ein ganzzahliger Wert). Mit zunehmender Periode steigt die Grundfrequenz
. Der Abstand entlang der Frequenzachse zwischen zwei benachbarten Spektrumskomponenten beträgt , und zwischen zwei Nullwerten (die Breite der Spektrumskeule) beträgt . Die Anzahl der harmonischen Komponenten innerhalb einer Keule, einschließlich des Nullwerts rechts in der Abbildung, beträgt , wobei das Vorzeichen das Runden auf die nächste ganze Zahl bedeutet, weniger (wenn das Tastverhältnis eine Bruchzahl ist) oder (wenn das Tastverhältnis eine Bruchzahl ist). ist ein ganzzahliger Wert). Mit zunehmender Periode steigt die Grundfrequenz  abnimmt, rücken die Spektralanteile im Diagramm näher zusammen, auch die Amplituden der Harmonischen nehmen ab. In diesem Fall bleibt die Form der Hülle erhalten.
abnimmt, rücken die Spektralanteile im Diagramm näher zusammen, auch die Amplituden der Harmonischen nehmen ab. In diesem Fall bleibt die Form der Hülle erhalten.




Bei der Lösung praktischer Probleme der Spektralanalyse werden zyklische Frequenzen anstelle von Kreisfrequenzen verwendet  , gemessen in Hertz. Offensichtlich beträgt der Abstand zwischen benachbarten Harmonischen im Diagramm , und die Breite einer Spektrumskeule beträgt . Diese Werte sind im Diagramm in Klammern dargestellt.
, gemessen in Hertz. Offensichtlich beträgt der Abstand zwischen benachbarten Harmonischen im Diagramm , und die Breite einer Spektrumskeule beträgt . Diese Werte sind im Diagramm in Klammern dargestellt.
In der praktischen Funktechnik werden in den meisten Fällen anstelle der Spektraldarstellung (Abb. 2.3, b) Spektraldiagramme der Amplituden- und Phasenspektren verwendet. Das Amplitudenspektrum einer Folge von Rechteckimpulsen ist in Abb. dargestellt. 2.3, c.
Offensichtlich ist die Hüllkurve des Amplitudenspektrums proportional  .
.
Was das Phasenspektrum (Abb. 2.3, d) betrifft, wird angenommen, dass sich die Anfangsphasen der harmonischen Komponenten sprunghaft um den Betrag ändern -π wenn sich das Vorzeichen des Umschlags ändert sinc kπ/q. Die Anfangsphasen der Harmonischen der ersten Keule werden als Null angenommen. Dann werden die Anfangsphasen der Harmonischen der zweiten Keule sein φ = -π , drittes Blütenblatt φ = -2π usw.
Betrachten wir eine andere Fourier-Reihendarstellung des Signals. Dazu verwenden wir die Eulersche Formel
 .
.
Nach dieser Formel lässt sich die k-te Komponente (2.9) der Signalentwicklung in eine Fourier-Reihe wie folgt darstellen
 ;
;  . (2.15)
. (2.15)
Hier sind die Größen und komplex und repräsentieren die komplexen Amplituden der Spektrumkomponenten. Dann die Serie
Fourier (2.8) unter Berücksichtigung von (2.14) wird die folgende Form annehmen
 , (2.16)
, (2.16)
 , (2.17)
, (2.17)
Es ist leicht zu überprüfen, dass die Entwicklung (2.16) anhand der Basisfunktionen durchgeführt wird  , die ebenfalls orthogonal auf dem Intervall sind
, die ebenfalls orthogonal auf dem Intervall sind  , d.h.
, d.h.

Ausdruck (2.16) ist komplexe Form Fourier-Reihe, die sich bis zu negativen Frequenzen erstreckt. Mengen und  , wobei das komplexe Konjugat einer Größe bezeichnet wird komplexe Amplituden Spektrum Weil eine komplexe Größe ist, folgt aus (2.15).
, wobei das komplexe Konjugat einer Größe bezeichnet wird komplexe Amplituden Spektrum Weil eine komplexe Größe ist, folgt aus (2.15).
 Und
Und  .
.
Dann bildet die Gesamtheit das Amplitudenspektrum und die Gesamtheit das Phasenspektrum des Signals.

In Abb. Abbildung 2.4 zeigt ein Spektraldiagramm des Spektrums der oben diskutierten Folge von Rechteckimpulsen, dargestellt durch eine komplexe Fourier-Reihe

Das Spektrum hat ebenfalls Liniencharakter, wird aber im Gegensatz zu den bisher betrachteten Spektren sowohl im Bereich positiver als auch im Bereich negativer Frequenzen bestimmt. Da es sich um eine gerade Funktion des Arguments handelt, ist das Spektraldiagramm symmetrisch um Null.
Basierend auf (2.15) können wir einen Zusammenhang zwischen den Koeffizienten und der Entwicklung (2.3) herstellen. Als
 Und
Und  ,
,
dann erhalten wir als Ergebnis
 . (2.18)
. (2.18)
Mit den Ausdrücken (2.5) und (2.18) können Sie die Werte in praktischen Berechnungen ermitteln.
Lassen Sie uns eine geometrische Interpretation der komplexen Form der Fourier-Reihe geben. Wählen wir die k-te Komponente des Signalspektrums aus. In komplexer Form wird die k-te Komponente durch die Formel beschrieben
wobei und durch Ausdrücke (2.15) bestimmt werden.
In der komplexen Ebene wird jeder der Terme in (2.19) als Längenvektoren dargestellt  , um einen Winkel und relativ zur realen Achse gedreht und mit der Frequenz in entgegengesetzte Richtungen rotierend (Abb. 2.5).
, um einen Winkel und relativ zur realen Achse gedreht und mit der Frequenz in entgegengesetzte Richtungen rotierend (Abb. 2.5).
Offensichtlich ergibt die Summe dieser Vektoren einen Vektor, der auf der realen Achse liegt und dessen Länge beträgt. Aber dieser Vektor entspricht der harmonischen Komponente


Was die Projektionen von Vektoren auf die imaginäre Achse betrifft, so haben diese Projektionen gleiche Längen, aber entgegengesetzte Richtungen und summieren sich zu Null. Dies bedeutet, dass in komplexer Form dargestellte Signale (2.16) tatsächlich reale Signale sind. Mit anderen Worten, die komplexe Form der Fourier-Reihe ist mathematisch eine Abstraktion, die sich sehr gut zur Lösung einer Reihe von Problemen der Spektralanalyse eignet. Daher wird manchmal das durch die trigonometrische Fourier-Reihe definierte Spektrum genannt physikalisches Spektrum, und die komplexe Form der Fourier-Reihe ist mathematisches Spektrum.
Abschließend betrachten wir die Frage der Energie- und Leistungsverteilung im Spektrum eines periodischen Signals. Dazu verwenden wir die Parseval-Gleichheit (1.42). Wenn das Signal zu einer trigonometrischen Fourier-Reihe entwickelt wird, nimmt der Ausdruck (1.42) die Form an
 .
.
Gleichstromenergie
 ,
,
und die Energie der k-ten Harmonischen
 .
.
Dann die Signalenergie
 . (2.20)
. (2.20)
Weil durchschnittliche Signalleistung
 ,
,
dann unter Berücksichtigung von (2.18)
 . (2.21)
. (2.21)
Wenn das Signal zu einer komplexen Fourier-Reihe entwickelt wird, nimmt der Ausdruck (1.42) die Form an
 ,
,
Wo  - Energie der k-ten Harmonischen.
- Energie der k-ten Harmonischen.
In diesem Fall die Signalenergie
 ,
,
und seine durchschnittliche Leistung
 .
.
Aus den obigen Ausdrücken folgt, dass die Energie oder durchschnittliche Leistung der k-ten Spektralkomponente des mathematischen Spektrums halb so groß ist wie die Energie oder Leistung der entsprechenden Spektralkomponente des physikalischen Spektrums. Dies liegt daran, dass das physikalische Spektrum gleichmäßig auf das mathematische Spektrum verteilt ist.
| -τ und /2 |
| τ und /2 |
| T |
| T |
| U 0 |
| S(t) |
Aufgabe Nr. 1, Gruppe RI – 210701
Periodische Folgen von Rechteckimpulsen werden in elektronischen Geräten häufig für verschiedene Anwendungen verwendet. Dabei handelt es sich um den Zusammenhang zwischen der Pulsdauer τ und der Schwingungsperiode T kann stark variieren. Zum Beispiel Vibrationen, die erzeugen Taktgeneratoren, die das „Tempo“ des Computerbetriebs bestimmen, sind durch vergleichbare Werte von τ und gekennzeichnet T, und die im Radar verwendeten Impulse können hunderte Male kürzer als die Periode sein. Attitüde T/τ heißt Tastverhältnis des Impulses, und der Umkehrwert (τ/ T) - Füllfaktor.
Reis. 6. Folge von Rechteckimpulsen (a) und Fourier-Reihenkoeffizienten (b)
Betrachten Sie eine Folge von Rechteckimpulsen mit einer Amplitude A, Dauer τ und nachfolgende mit Periode T(Abb. 6, A). Wählen wir den Beginn der Zeitzählung wie in der Abbildung gezeigt, also so, dass der Impuls symmetrisch zur Nullmarke ist, und berechnen wir die Koeffizienten der Fourier-Reihe (1). Da die Funktion S(T) mit dieser Position der Achsen erweist sich als gerade, alle B N gleich Null sind und für A N wir bekommen:
Die Fourier-Reihe für eine Folge von Rechteckimpulsen hat die Form:
 (6)
(6)
Die mit den Formeln (5) berechneten Werte der Koeffizienten der Fourier-Reihe sind im Spektraldiagramm in Abb. dargestellt. 6, B.
Chancen A N kann mit einer Funktion verknüpft werden  . Tatsächlich sind sie proportional (mit dem Faktor
. Tatsächlich sind sie proportional (mit dem Faktor  ) Funktionswerte
) Funktionswerte  mit Argumenten, die harmonischen Frequenzen entsprechen. Dies lässt sich erkennen, wenn Ausdruck (5) wie folgt umgeschrieben wird:
mit Argumenten, die harmonischen Frequenzen entsprechen. Dies lässt sich erkennen, wenn Ausdruck (5) wie folgt umgeschrieben wird:
 (7)
(7)
Also eine Funktion wie  Ist Umschlag für Koeffizienten Fourier-Entwicklungen Folgen von Rechteckimpulsen (siehe Abb. 6, B). Position der Hüllkurvennullpunkte auf der Frequenzachse F kann aus der Bedingung entnommen werden
Ist Umschlag für Koeffizienten Fourier-Entwicklungen Folgen von Rechteckimpulsen (siehe Abb. 6, B). Position der Hüllkurvennullpunkte auf der Frequenzachse F kann aus der Bedingung entnommen werden  oder
oder  , Wo. Beim ersten Mal geht die Hüllkurve bei der Frequenz auf Null F= 1/τ (oder ω = 2π/τ). Als nächstes werden die Nullen der Hüllkurve wiederholt F= 2/τ, 3/τ usw. Diese Frequenzen können (mit ganzzahligen Arbeitszyklen) mit den Frequenzen beliebiger Spektrumharmonischer zusammenfallen, und diese Frequenzkomponenten aus der Fourier-Reihe verschwinden. Wenn das Tastverhältnis eine ganze Zahl ist, die Periode T genau ein Vielfaches der Pulsdauer. Dann liegen zwischen den beiden Nullstellen der Hüllkurve Spektrumsharmonische in der Höhe vor Q-
1.
, Wo. Beim ersten Mal geht die Hüllkurve bei der Frequenz auf Null F= 1/τ (oder ω = 2π/τ). Als nächstes werden die Nullen der Hüllkurve wiederholt F= 2/τ, 3/τ usw. Diese Frequenzen können (mit ganzzahligen Arbeitszyklen) mit den Frequenzen beliebiger Spektrumharmonischer zusammenfallen, und diese Frequenzkomponenten aus der Fourier-Reihe verschwinden. Wenn das Tastverhältnis eine ganze Zahl ist, die Periode T genau ein Vielfaches der Pulsdauer. Dann liegen zwischen den beiden Nullstellen der Hüllkurve Spektrumsharmonische in der Höhe vor Q-
1.
Tabelle 1 veranschaulicht, wie Pulsparameter in Zeit- und Frequenzdarstellungen zusammenhängen. 2. Mit zunehmender Periode T Die Harmonischen im Spektraldiagramm rücken näher zusammen (das Spektrum wird „dicker“). Eine Änderung nur der Periode ändert jedoch nicht die Form der Amplitudenspektrum-Hüllkurve. Die Entwicklung der Hüllkurve (die Verschiebung ihrer Nullstellen) hängt von der Impulsdauer ab. Hier wird die Entwicklung von Amplitudenspektraldiagrammen für Sequenzen von Rechteckimpulsen gezeigt, deren Impulsdauer und -periode variieren. Die Ordinatenachsen der Spektraldiagramme zeigen die relativen Werte der harmonischen Amplituden:  Sie werden nach den Formeln berechnet:
Sie werden nach den Formeln berechnet:
 (8)
(8)
Tabelle 2. Oszillogramme und Spektrogramme von Folgen von Rechteckimpulsen

2.5. Spektren chaotischer (Rauschen-)Schwingungen
Chaotische Schwingung S(T) - Das zufälliger Prozess. Jede seiner Implementierungen unter konstanten Bedingungen wiederholt sich nicht und ist einzigartig. In der Elektronik sind chaotische Schwingungen damit verbunden Lärm- Schwankungen von Strömen und Spannungen, die sich aufgrund der zufälligen Bewegung von Ladungsträgern zufällig ändern. In diesem Zusammenhang werden chaotische und Lärmschwingungen synonym betrachtet.
Reis. 7. Blockdiagramm zur Messung der mittleren quadratischen Rauschspannung
Lärmschwankung kann in der Frequenzdarstellung beschrieben werden: Sie ist einer bestimmten spektralen Charakteristik zugeordnet und für einen Zufallsprozess kontinuierlich. Die theoretischen Grundlagen der spektralen Zerlegung chaotischer Schwingungen werden in dargestellt. Ohne in eine strenge Theorie einzutauchen, erklären wir die Methodik zur experimentellen Untersuchung statistischer Parameter Rauschspannung S(T) gemäß dem Diagramm in Abb. 8.
R  Ist. 8. Schema zur Messung der spektralen Dichte der Rauschspannungsintensität
Ist. 8. Schema zur Messung der spektralen Dichte der Rauschspannungsintensität
Lassen wir die Rauschspannung weg S(T) durch einen Filter, der Schwingungsenergie in einem schmalen Band freisetzt  in der Nähe der Frequenz F. Wenn die Bedingung erfüllt ist
in der Nähe der Frequenz F. Wenn die Bedingung erfüllt ist  <<
F Die Schwingung am Filterausgang ähnelt einer Sinuskurve mit einer Frequenz F. Allerdings unterliegen Amplitude und Phase dieser Sinuskurve chaotischen Veränderungen. Mit abnehmender Filterbandbreite
<<
F Die Schwingung am Filterausgang ähnelt einer Sinuskurve mit einer Frequenz F. Allerdings unterliegen Amplitude und Phase dieser Sinuskurve chaotischen Veränderungen. Mit abnehmender Filterbandbreite  die Form der Ausgangsschwingung nähert sich zunehmend einer Sinuskurve. Seine Amplitude nimmt ab, aber das Verhältnis der mittleren quadratischen Spannung, die durch den Filter geht (
die Form der Ausgangsschwingung nähert sich zunehmend einer Sinuskurve. Seine Amplitude nimmt ab, aber das Verhältnis der mittleren quadratischen Spannung, die durch den Filter geht (  ), zur Bandbreite
), zur Bandbreite  bleibt endlich und tendiert mit sukzessiver Abnahme des Bandes zu einer bestimmten Grenze W(F):
bleibt endlich und tendiert mit sukzessiver Abnahme des Bandes zu einer bestimmten Grenze W(F):
Grenzwert W(F) werden genannt spektrale Intensitätsdichte Verfahren S(T).
Sie entspricht der durchschnittlichen Intensität der harmonischen Komponenten pro Intervalleinheit der Frequenzachse. Beim Messen W(F) verwenden einen schmalbandigen abstimmbaren Filter, der auf jede beliebige Frequenz innerhalb eines bestimmten Messbereichs abgestimmt werden kann. Die durch den Filter laufende Rauschspannung wird einer quadratischen Erfassung unterzogen und gemittelt (integriert). Das Ergebnis ist ein durchschnittliches Quadrat:  . Weiter entlang des bekannten Filterbandes
. Weiter entlang des bekannten Filterbandes  Berechnung W(F).
Volle Intensität des Prozesses- durchschnittliches Quadrat
Berechnung W(F).
Volle Intensität des Prozesses- durchschnittliches Quadrat  - gefunden durch Integration der Spektralkomponenten des Rauschens über alle Frequenzen:
- gefunden durch Integration der Spektralkomponenten des Rauschens über alle Frequenzen:
 (10)
(10)
Um sich auf die Arbeit vorzubereiten, sollten Sie dieses Handbuch vollständig lesen. Ausführlichere Informationen zum Thema Laborarbeit finden Sie im Kapitel „Frequenzspektren elektrischer Schwingungen, Spektralanalyse“ des Buches.
Eine periodische Folge rechteckiger Videoimpulse ist eine Modulationsfunktion für die Bildung einer periodischen Folge rechteckiger Radioimpulse (PPRP), bei denen es sich um Sondierungssignale zur Erkennung und Messung der Koordinaten sich bewegender Ziele handelt. Mithilfe des Spektrums der Modulationsfunktion (PPVI) ist es daher relativ einfach und schnell möglich, das Spektrum des Sondierungssignals (PPVI) zu bestimmen. Wenn ein Sondierungssignal von einem sich bewegenden Ziel reflektiert wird, ändern sich die Frequenzen des harmonischen Spektrums der Trägerschwingung (Doppler-Effekt). Dadurch ist es möglich, ein von einem sich bewegenden Ziel reflektiertes Nutzsignal vor dem Hintergrund störender (Interferenz-)Schwingungen zu identifizieren, die von stationären Objekten (lokalen Objekten) oder sich langsam bewegenden Objekten (meteorologische Formationen, Vogelschwärme usw.) reflektiert werden. .
PPPVI (Abb. 1.42) ist eine Reihe einzelner rechteckiger Videoimpulse, die in gleichen Zeitintervallen aufeinander folgen. Analytischer Ausdruck des Signals.
wo ist die Pulsamplitude; – Pulsdauer; – Pulswiederholungsperiode; – Pulswiederholungsrate, ; - Auslastungsgrad.
Um die spektrale Zusammensetzung einer periodischen Impulsfolge zu berechnen, wird die Fourier-Reihe verwendet. Mit bekannten Spektren einzelner Impulse, die eine periodische Folge bilden, können wir die Beziehung zwischen der spektralen Dichte der Impulse und den komplexen Amplituden der Reihe nutzen:
Für einen einzelnen rechteckigen Videoimpuls wird die spektrale Dichte durch die Formel beschrieben
Mithilfe der Beziehung zwischen der spektralen Dichte eines einzelnen Impulses und den komplexen Amplituden der Reihe finden wir Folgendes:
wo = 0; ± 1; ± 2; ...
Das Amplituden-Frequenz-Spektrum (Abb. 1.43) wird durch eine Reihe von Komponenten dargestellt:
In diesem Fall entsprechen positive Werte Anfangsphasen von Null und negative Werte entsprechen Anfangsphasen gleich .
Somit ist der analytische Ausdruck für PPPVI gleich
Aus der Analyse der in Abbildung 1.43 dargestellten Diagramme folgt:
· Das PPPVI-Spektrum ist diskret und besteht aus einzelnen Harmonischen mit der Frequenz .
· Der ASF-Umschlag ändert sich je nach Gesetz.
· Der Maximalwert der Hüllkurve bei ist gleich dem Wert der konstanten Komponente.
· Die Anfangsphasen der Harmonischen innerhalb der ungeraden Keulen sind gleich 0, innerhalb der geraden Keulen.
· Die Anzahl der Harmonischen innerhalb jeder Keule ist gleich.
Breite des Signalspektrums bei 90 % der Signalenergie
· Signalbasis, daher ist das Signal einfach.
Wenn Sie die Dauer der Impulse oder deren Wiederholungsfrequenz ändern F(Periode), dann ändern sich die Parameter des Spektrums und sein ASF.
Abbildung 1.43 zeigt ein Beispiel für eine Änderung des Signals und seiner ASF bei Verdoppelung der Pulsdauer.
Periodische Folgen rechteckiger Videoimpulse und ihre ASF-Parameter, T,. Und , T, sind in Abbildung 1.44 dargestellt.
Aus der Analyse der angegebenen Diagramme folgt:
1. Für PPPVI mit Pulsdauer:
· Einschaltdauer Q=4, daher sind in jeder Keule 3 Harmonische konzentriert;
· Frequenz der k-ten Harmonischen;
· Breite des Signalspektrums bei 90 % Energieniveau;
Die konstante Komponente ist gleich
2. Für PPPVI mit Pulsdauer:
· Einschaltdauer q= 2, daher gibt es in jedem Lappen 1 Harmonische;
· Die Frequenz der k-ten Harmonischen bleibt unverändert;
· Die Breite des Signalspektrums bei 90 % seiner Energie verringerte sich um das Zweifache;
· Die konstante Komponente wurde um das Zweifache erhöht.
Daraus können wir schließen, dass mit zunehmender Pulsdauer die ASF entlang der Ordinatenachse „komprimiert“ wird (die Breite des Signalspektrums nimmt ab), während die Amplituden der Spektralkomponenten zunehmen. Die harmonischen Frequenzen ändern sich nicht.
In Abbildung 1.44. Es wird ein Beispiel für eine Änderung des Signals und seiner ASF mit einer Erhöhung der Wiederholungsperiode um das Vierfache (eine Verringerung der Wiederholungsrate um das Vierfache) vorgestellt.
c) die Breite des Signalspektrums hat sich bei 90 % seiner Energie nicht verändert;
d) die konstante Komponente verringerte sich um das Vierfache.
Daraus können wir schließen, dass mit zunehmender Wiederholungsperiode (Abnahme der Wiederholungsfrequenz) eine „Komprimierung“ im ASF entlang der Frequenzachse auftritt (die Amplituden der Harmonischen nehmen mit zunehmender Anzahl innerhalb jeder Keule ab). . Die Breite des Signalspektrums ändert sich nicht. Eine weitere Verringerung der Wiederholfrequenz (Erhöhung der Wiederholperiode) führt (bei ) zu einer Abnahme der Amplituden der Harmonischen auf verschwindend kleine Werte. In diesem Fall wird das Signal zu einem einzigen und dementsprechend wird das Spektrum kontinuierlich.
Die spektrale Darstellung von Zeitfunktionen wird in der Kommunikationstheorie häufig verwendet. Für theoretische und experimentelle Untersuchungen der Eigenschaften elektrischer Schaltkreise und der Übertragung von Nachrichten über Kommunikationskanäle werden verschiedene Arten von Signalen verwendet: harmonische Schwingungen, konstante Spannungspegel, Folgen von Rechteck- und Funkimpulsen usw. Rechensignale in Form von a Einheitsfunktionen spielen eine besonders wichtige Rolle bei theoretischen Untersuchungen elektrischer Schaltkreise und Impulsfunktionen (Dirac-Funktion). Lassen Sie uns die Spektren der häufigsten typischen Signale bestimmen.
11.1 Spektrum einer Folge von Rechteckimpulsen
Es gebe eine periodische Folge von Rechteckimpulsen mit der Periode T, der Impulsdauer t und der Amplitude A. Der analytische Ausdruck der Funktion, die den Impuls auf dem Segment beschreibt, hat die Form
 (11.1)
(11.1)
Ein Diagramm einer periodischen Impulsfolge ist in Abbildung 11.1 dargestellt.

Abbildung 11.1
Diese Funktion ist gerade, da ihr Graph symmetrisch zur Ordinate ist. Dann werden die Fourier-Koeffizienten dieser Funktionen mithilfe der Formeln (KFT2) berechnet, wobei .

Die Zahl stellt den Durchschnittswert der Funktion über einen Zeitraum dar und wird als konstante Komponente bezeichnet. Die Frequenz wird als Grundwelle oder erste Harmonische bezeichnet, und die k Frequenzen werden als höhere Harmonische bezeichnet, wobei k = 2,3,4,...
Konstruieren wir das Amplitudenspektrum der betrachteten Folge von Rechteckimpulsen. Da die Funktion periodisch ist, ist ihr Amplitudenspektrum linear. Bezeichnen wir mit dem Abstand zwischen benachbarten Harmonischen. Offensichtlich ist es gleich. Die Amplitude der k-ten Harmonischen hat nach (11.2) die Form
 (11.3)
(11.3)
Finden wir die Beziehung zwischen der Periode T und der Impulsdauer, bei der die Amplitude der k-ten Harmonischen Null wird.
A 2 ≈32V, A 3 ≈15V, A 4 ≈0, A 5 ≈6,36V, A 6 ≈10,5V, A 7 ≈6,36V, A 8 ≈0, A 9 ≈4,95V, A 10 ≈6,37V.
Das als Ergebnis der Berechnung erhaltene Amplitudenspektrum ist in Abbildung 11.2 dargestellt.

Abbildung 11.2
Ein solches Spektrum wird als Linien- oder diskretes Spektrum bezeichnet.
Die Spektren für q=8 und q=16 wurden auf ähnliche Weise berechnet und aufgezeichnet. Sie sind in den Abbildungen 11.3 bzw. 11.4 dargestellt.

Abbildung 11.3

Abbildung 11.4
Aus der Abbildung ist ersichtlich, dass die Amplitude der ersten Harmonischen umso kleiner ist, je größer das Tastverhältnis der Rechteckimpulse ist, das Spektrum jedoch umso langsamer abnimmt.
11.2 Spektrum eines einzelnen Rechteckimpulses
Betrachten wir Ф (11.1) für den Fall, dass T→∞, also eine periodische Folge von Impulsen, in einen einzelnen Rechteckimpuls der Dauer t u entartet.
Der analytische Ausdruck für diesen Impuls wird wie folgt geschrieben:
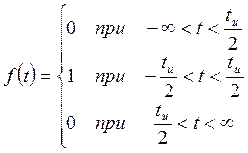
Der Graph dieser Funktion ist in Abbildung 11.5 dargestellt.

Abbildung 11.5
In diesem Fall werden die Frequenz der ersten Harmonischen und der Abstand zwischen den Harmonischen gleich 0, daher wechselt das Spektrum von diskret zu kontinuierlich und besteht aus einer unendlich großen Anzahl von Spektrallinien, die sich in unendlich kleinen Abständen voneinander befinden. Ein solches Spektrum nennt man kontinuierlich. Daraus ergibt sich die wichtigste Regel: Periodische Signale erzeugen diskrete Spektren und nichtperiodische Signale erzeugen kontinuierliche Spektren.
Das Spektrum eines rechteckigen Einzelimpulses kann direkt aus der direkten Fourier-Transformation (10.1) ermittelt werden.
