ВЛАСТИВОСТІ ФУНКЦІЙ, НЕПРЕРИВНИХ НА ВІДРІЗКУ

Розглянемо деякі властивості безперервних функцій на відрізку. Ці властивості наведемо без підтвердження.

функцію y = f(x)називають безперервний на відрізку [a, b], якщо вона безперервна переважають у всіх внутрішніх точках цього відрізка, але в його кінцях, тобто. у точках aі b, безперервна відповідно праворуч і ліворуч.

Теорема 1.Функція безперервна на відрізку [ a, b], хоча в одній точці цього відрізка набуває найбільшого значення і хоча в одній – найменше.

Теорема стверджує, що якщо функція y = f(x)безперервна на відрізку [ a, b], то знайдеться хоча б одна точка x 1 Î [ a, b] така, що значення функції f(x)у цій точці буде найбільшим із усіх її значень на цьому відрізку: f(x 1) ≥ f(x). Аналогічно знайдеться така точка x 2, В якій значення функції буде найменшим зі всіх значень на відрізку: f(x 1) ≤ f(x).

Зрозуміло, що таких точок може бути і кілька, наприклад, на малюнку показано, що функція f(x)приймає найменше значення у двох точках x 2і x 2 ".

Зауваження. Твердження теореми можна стати невірним, якщо розглянути значення функції на інтервалі ( a, b). Справді, якщо розглянути функцію y = xна (0, 2), то вона безперервна на цьому інтервалі, але не досягає в ньому ні найбільшого, ні найменшого значень: вона досягає цих значень на кінцях інтервалу, але кінці не належать нашій області.

Також теорема перестає бути вірною для розривних функцій. Наведіть приклад.

Слідство.Якщо функція f(x)безперервна на [ a, b], вона обмежена цьому відрізку.

Теорема 2.Нехай функція y = f(x)безперервна на відрізку [ a, b] і на кінцях цього відрізка набуває значення різних знаків, тоді всередині відрізка знайдеться принаймні одна точка x = C, В якій функція звертається в нуль: f(C)= 0 де а< C< b

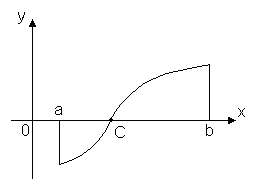
Ця теорема має простий геометричний зміст: якщо точки графіка безперервної функції y = f(x), що відповідають кінцям відрізка [ a, b] лежать по різні боки від осі Ox, то цей графік хоча б в одній точці відрізка перетинає вісь Ox. Розривні функції цією властивістю можуть не мати.

Ця теорема припускає таке узагальнення.

Теорема 3 (теорема про проміжні значення).Нехай функція y = f(x)безперервна на відрізку [ a, b] та f(a) = A, f(b) = B. Тоді для будь-якого числа C, укладеного між Aі B, знайдеться всередині цього відрізку така точка CÎ [ a, b], що f(c) = C.

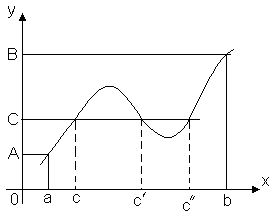
Ця теорема геометрично очевидна. Розглянемо графік функції y = f(x). Нехай f(a) = A, f(b) = B. Тоді будь-яка пряма y = C, де C– будь-яке число, укладене між Aі B, перетне графік функції, принаймні, в одній точці. Абсцис точки перетину і буде тим значенням x = C, за якого f(c) = C.

Таким чином, безперервна функція, переходячи від одного свого значення до іншого, обов'язково проходить через усі проміжні значення. Зокрема:

Слідство.Якщо функція y = f(x)безперервна на деякому інтервалі і набуває найбільшого і найменшого значення, то на цьому інтервалі вона набуває, принаймні, один раз будь-яке значення, укладене між її найменшим і найбільшим значеннями.

ВИРОБНИЧА І ЇЇ ДОДАТКИ. ВИЗНАЧЕННЯ ВИРОБНИЧОЇ

Нехай маємо деяку функцію y=f(x),визначену на деякому проміжку. Для кожного значення аргументу xз цього проміжку функція y=f(x)має певне значення.

Розглянемо два значення аргументу: вихідне x 0 та нове x.

Різниця x-x 0 називається збільшенням аргументу xу точці x 0 і позначається Δx. Таким чином, Δx = x – x 0 (приріст аргументу може бути як позитивним, і негативним). З цієї рівності випливає, що x=x 0 +Δx, тобто. первісне значення змінної набуло деякого збільшення. Тоді, якщо у точці x 0 значення функції було f(x 0 ), то в новій точці xфункція прийматиме значення f(x) = f(x 0 +Δx).

Різниця y – y 0 = f(x) – f(x 0 ) називається збільшенням функції y = f(x)у точці x 0 і позначається символом Δy. Таким чином,

Зазвичай вихідне значення аргументу x 0 вважається фіксованим, а нове значення x- Змінним. Тоді y 0 = f(x 0 ) виявляється постійною, а y = f(x)- Змінною. Прирощення Δyі Δxтакож будуть змінними і формула (1) показує, що Dyє функцією змінної Δx.

Складемо відношення збільшення функції до збільшення аргументу

Знайдемо межу цього відношення при Δx→0. Якщо ця межа існує, то її називають похідною цієї функції f(x)у точці x 0 і позначають f "(x 0). Отже,

Похіднийданої функції y = f(x)у точці x 0 називається межа відношення збільшення функції Δ yдо збільшення аргументу Δ xколи останнє довільним чином прагне до нуля.

Зауважимо, що для однієї і тієї ж функції похідна у різних точках xможе набувати різних значень, тобто. похідну можна розглядати як функцію аргументу x. Ця функція позначається f "(x)

Похідна позначається символами f "(x),y", . Конкретне значення похідної при x = aпозначається f "(a) або y "| x=a.

Операція знаходження похідної від функції f(x)називається диференціюванням цієї функції.

Для безпосереднього знаходження похідної за визначенням можна застосувати таке практичне правило:

приклади.

МЕХАНІЧНИЙ ДУМКА ВИРОБНИЧОЇ

З фізики відомо, що закон рівномірного руху має вигляд s = v·t, де s– шлях, пройдений на момент часу t, v- Швидкість рівномірного руху.

Проте, т.к. більшість рухів, що відбуваються в природі, нерівномірно, то в загальному випадку швидкість, а, отже, і відстань sбуде залежати від часу t, тобто. буде функцією часу.

Отже, нехай матеріальна точка рухається прямою в одному напрямку за законом s = s (t).

Зазначимо деякий момент часу t 0 . До цього моменту точка пройшла шлях s = s (t 0 ). Визначимо швидкість vматеріальної точки на момент часу t 0 .

Для цього розглянемо якийсь інший момент часу t 0 + Δ t. Йому відповідає пройдений шлях s = s (t 0 + Δ t). Тоді за проміжок часу Δ tточка пройшла шлях Δs = s (t 0 + Δ t)–s(t).

Розглянемо ставлення. Воно називається середньою швидкістю у проміжку часу Δ t. Середня швидкість не може точно охарактеризувати швидкість переміщення точки в момент t 0 (т.к. рух нерівномірний). Для того, щоб точніше виразити цю дійсну швидкість за допомогою середньої швидкості, потрібно взяти менший проміжок часу Δ t.

Отже, швидкістю руху в даний момент часу t 0 (миттєвою швидкістю) називається межа середньої швидкості в проміжку від t 0 до t 0 +Δ t, коли Δ t→0:

,

тобто. швидкість нерівномірного рухуце похідна від пройденого шляху за часом.

ГЕОМЕТРИЧНИЙ ДУМКА ВИРОБНИЧОЇ

Введемо спочатку визначення дотичної до кривої у цій точці.

Нехай маємо криву та на ній фіксовану точку М 0(див. малюнок). Розглянемо іншу точку Мцією кривою і проведемо січну M 0 M. Якщо точка Мпочинає переміщатися кривою, а точка М 0залишається нерухомою, то січка змінює своє становище. Якщо при необмеженому наближенні точки Мпо кривій до точки М 0з будь-якої сторони січка прагне зайняти становище певної прямої М 0 Т, то пряма М 0 Тназивається дотичною до кривої в даній точці М 0.

Т.о., дотичноїдо кривої в даній точці М 0називається граничне положення сіючої М 0 М, коли точка Мпрагне вздовж кривої до точки М 0.

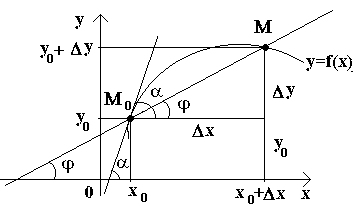
Розглянемо тепер безперервну функцію y=f(x)та відповідну цій функції криву. За деякого значення х 0 функція набуває значення y 0 = f (x 0).Цим значенням x 0 та y 0 на кривій відповідає точка М 0 (x 0; y 0).Дамо аргументу x 0приріст Δ х. Новому значенню аргументу відповідає нарощене значення функції y 0 +Δ y=f(x 0 –Δ x). Отримуємо точку М(x 0+Δ x; y 0+Δ y).Проведемо січну М 0 Мі позначимо через φ кут, утворений січною з позитивним напрямом осі Ox. Складемо відношення та зауважимо, що .

Якщо тепер Δ x→0, то через безперервність функції Δ у→0, і тому точка М, переміщаючись кривою, необмежено наближається до точки М 0. Тоді січуча М 0 Мбуде прагнути зайняти становище дотичної до кривої в точці М 0, а кут φ→α при Δ x→0, де через α позначили кут між дотичним та позитивним напрямком осі Ox. Оскільки функція tg φ безперервно залежить від φ при φ≠π/2 то при φ→α tg φ → tg α і, отже, кутовий коефіцієнт дотичної буде:

тобто. f "(x)= tg α.

Т.о., геометрично у "(x 0)представляє кутовий коефіцієнт щодо графіку цієї функції в точці x 0, тобто. при даному значенні аргументу x, похідна дорівнює тангенсукута, утвореного щодо графіку функції f(x)у відповідній точці М 0 (x; y)з позитивним напрямом осі Ox.

приклад.Знайти кутовий коефіцієнт дотичної до кривої у = х 2 у точці М(-1; 1).

Раніше ми вже бачили, що ( x 2)" = 2х. Але кутовий коефіцієнт щодо кривої є tg α = y"| x = -1 = - 2.

ДИФЕРЕНЦІЙНІСТЬ ФУНКЦІЙ. НЕПРЕРИВНІСТЬ ДИФЕРЕНЦІЙНОЇ ФУНКЦІЇ

Функція y=f(x)називається диференційованоїв деякій точці x 0 якщо вона має в цій точці певну похідну, тобто. якщо межа відношення існує і кінцевий.

Якщо функція диференційована у кожній точці деякого відрізка [ а; b] або інтервалу ( а; b), то кажуть, що вона диференційованана відрізку [ а; b] або відповідно в інтервалі ( а; b).

Справедлива наступна теорема, що встановлює зв'язок між диференційованими та безперервними функціями.

Теорема.Якщо функція y=f(x)диференційована в деякій точці x 0, то вона у цій точці безперервна.

Таким чином, з диференційованості функції випливає її безперервність.

Доведення. Якщо , то

,

де α нескінченно мала величина, тобто. величина, що прагне нуля при Δ x→0. Але тоді

Δ y=f "(x 0) Δ x+αΔ x=> Δ y→0 при Δ x→0, тобто f(x) – f(x 0)→0 при x→x 0 , а це означає, що функція f(x)безперервна в точці x 0 . Що й потрібно було довести.

Таким чином, у точках розриву функція не може мати похідну. Зворотне твердження неправильне: існують безперервні функції, які у деяких точках є диференційованими (тобто. не мають у цих точках похідної).

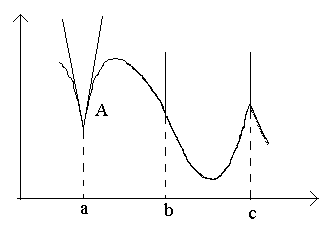
Розглянемо малюнку точки а, b, c.

У точці aпри Δ x→0 відношення не має межі (бо односторонні межі різні при Δ x→0–0 та Δ x→0+0). У точці Aграфіка немає певної дотичної, але є дві різні односторонні дотичні з кутовими коефіцієнтами до 1 і до 2 . Такий тип точок називають кутовими точками.

У точці bпри Δ x→0 відношення є знакопостійною нескінченно великою величиною. Функція має нескінченну похідну. У цій точці графік має вертикальну дотичну. Тип точки - "точка перегину" вертикальної дотичної.

У точці cодносторонні похідні є нескінченно більшими величинами різних знаків. У цій точці графік має дві злиті вертикальні дотичні. Тип - "точка повернення" з вертикальної дотичної - окремий випадок кутової точки.

На рисунках нижче показано, де функція може досягати найменшого та найбільшого значення. На лівому малюнку найменше та найбільше значення зафіксовано у точках локального мінімуму та максимуму функції. На правому малюнку – на кінцях відрізка.

Якщо функція y = f(x) безперервна на відрізку [ a, b] , то вона досягає на цьому відрізку найменшого і найбільшого значень . Це, як говорилося, може статися чи точках екстремуму, або кінцях відрізка. Тому для знаходження найменшого і найбільшого значень функції , безперервний на відрізку [ a, b], потрібно обчислити її значення у всіх критичних точкахі на кінцях відрізка, а потім вибрати з них найменше та найбільше.

Нехай, наприклад, потрібно визначити найбільше значення функції f(x) на відрізку [ a, b]. Для цього слід знайти всі її критичні точки, що лежать на [ a, b] .

Критичною точкою називається точка, в якій функція визначена, а її похіднаабо дорівнює нулю, або немає. Потім слід обчислити значення функції критичних точках. І, нарешті, слід порівняти між собою за величиною значення функції в критичних точках і кінцях відрізка ( f(a) та f(b)). Найбільше з цих чисел і буде найбільшим значенням функції на відрізку [a, b] .

Аналогічно вирішуються завдання на перебування найменших значень функції .

Шукаємо найменше та найбільше значення функції разом

Приклад 1. Знайти найменше та найбільше значення функції на відрізку [-1, 2] .

Рішення. Знаходимо похідну цієї функції. Прирівняємо похідну нулю () та отримаємо дві критичні точки: і . Для знаходження найменшого та найбільшого значень функції на заданому відрізку достатньо обчислити її значення на кінцях відрізка і в точці, оскільки точка не належить відрізку [-1, 2]. Ці значення функції - такі: , , . З цього виходить що найменше значення функції(на графіці нижче позначено червоним), що дорівнює -7, досягається на правому кінці відрізка - у точці , а найбільше(теж червоне на графіці), дорівнює 9, - у критичній точці .

Якщо функція безперервна в деякому проміжку і цей проміжок не є відрізком (а є, наприклад, інтервалом; різниця між інтервалом та відрізком: граничні точки інтервалу не входять до інтервалу, а граничні точки відрізка входять у відрізок), то серед значень функції може і не бути найменшого та найбільшого. Так, наприклад, функція, зображена на малюнку нижче, безперервна на ]-∞, +∞[ і не має найбільшого значення.

Однак для будь-якого проміжку (закритого, відкритого чи нескінченного) справедлива наступна властивість безперервних функцій.

Для самоперевірки при розрахунках можна скористатися онлайн похідних калькулятором .

Приклад 4. Знайти найменше та найбільше значення функції на відрізку [-1, 3] .

Рішення. Знаходимо похідну цієї функції як похідну приватного:

.

Прирівнюємо похідну нулю, що дає одну критичну точку: . Вона належить відрізку [-1, 3]. Для знаходження найменшого та найбільшого значень функції на заданому відрізку знаходимо її значення на кінцях відрізка та в знайденій критичній точці:

Порівнюємо ці значення. Висновок: , рівного -5/13, у точці та найбільшого значення, рівного 1, у точці .

Продовжуємо шукати найменше та найбільше значення функції разом

Існують викладачі, які на тему знаходження найменшого і максимального значень функції не дають студентам на вирішення приклади складніше щойно розглянутих, тобто таких, у яких функція - многочлен чи дріб, чисельник і знаменник якої - многочлены. Але ми не обмежимося такими прикладами, оскільки серед викладачів бувають любителі змусити студентів думати по повній (таблиці похідних). Тому в хід підуть логарифм та тригонометрична функція.

Приклад 8. Знайти найменше та найбільше значення функції на відрізку .

Рішення. Знаходимо похідну цієї функції як похідну твори :

Прирівнюємо похідну нулю, що дає одну критичну точку: . Вона належить відрізку. Для знаходження найменшого та найбільшого значень функції на заданому відрізку знаходимо її значення на кінцях відрізка та в знайденій критичній точці:

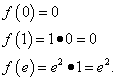
Результат усіх дій: функція досягає найменшого значення, рівного 0, у точці та в точці та найбільшого значення, рівного e², у точці.

Для самоперевірки при розрахунках можна скористатися онлайн похідних калькулятором .

Приклад 9. Знайти найменше та найбільше значення функції на відрізку .

Рішення. Знаходимо похідну цієї функції:

Прирівнюємо похідну нулю:

Єдина критична точка належить відрізку. Для знаходження найменшого та найбільшого значень функції на заданому відрізку знаходимо її значення на кінцях відрізка та в знайденій критичній точці:

Висновок: функція досягає найменшого значення, рівного , у точці та найбільшого значення, рівного , у точці .

У прикладних екстремальних задачах знаходження найменшого (найбільшого) значень функції, як правило, зводиться до знаходження мінімуму (максимуму). Але більший практичний інтерес мають самі мінімуми чи максимуми, а ті значення аргументу, у яких досягаються. При вирішенні прикладних завдань виникає додаткова труднощі - складання функцій, що описують явище, що розглядається, або процес.

приклад 10.Резервуар ємністю 4 має форму паралелепіпеда з квадратною основою і відкритий зверху, потрібно вилудити оловом. Якими мають бути розміри резервуара, щоб на його покриття пішла найменша кількість матеріалу?

Рішення. Нехай x- сторона основи, h- Висота резервуара, S- площа поверхні без кришки, V- Його обсяг. Площа поверхні резервуара виражається формулою, тобто. є функцією двох змінних. Щоб виразити Sяк функцію однієї змінної, скористаємося тим, що , звідки . Підставивши знайдений вираз hу формулу для S:

Досліджуємо цю функцію на екстремум. Вона визначена і диференційована всюди ]0, +∞[ , причому

.

Прирівнюємо похідну нулю () і знаходимо критичну точку. Крім того, при похідна не існує, але це значення не входить в область визначення і тому не може бути точкою екстремуму. Отже, єдина критична точка. Перевіримо її на наявність екстремуму, використовуючи другу достатню ознаку. Знайдемо другу похідну. При другому похідному більше нуля (). Значить, при функція досягає мінімуму . Оскільки цей мінімум - єдиний екстремум цієї функції, і є її найменшим значенням. Отже, сторона основи резервуара повинна дорівнювати 2 м, а його висота .

Для самоперевірки при розрахунках можна скористатися

З практичної точки зору найбільший інтерес представляє використання похідної для знаходження найбільшого та найменшого значення функції. З чим це пов'язано? Максимізація прибутку, мінімізація витрат, визначення оптимального завантаження устаткування... Інакше кажучи, у багатьох сферах життя доводиться вирішувати завдання оптимізації будь-яких параметрів. А це і є завдання на знаходження найбільшого та найменшого значення функції.

Слід зазначити, що найбільше і найменше значення функції зазвичай шукається на деякому інтервалі X , який є всією областю визначення функції або частиною області визначення. Сам інтервал X може бути відрізком, відкритим інтервалом , нескінченним проміжком.

У цій статті ми говоритимемо про знаходження найбільшого та найменшого значень явно заданої функції однієї змінної y=f(x) .

Навігація на сторінці.

Найбільше та найменше значення функції – визначення, ілюстрації.

Стисло зупинимося на основних визначеннях.

Найбільшим значенням функції , що для будь-кого справедлива нерівність.

Найменшим значенням функції y=f(x) на проміжку X називають таке значення , що для будь-кого справедлива нерівність.

Ці визначення інтуїтивно зрозумілі: найбільше (найменше) значення функції - це найбільше (маленьке) значення, що приймається на аналізованому інтервалі при абсцисі.

Стаціонарні точки– це значення аргументу, у яких похідна функції перетворюється на нуль.

Для чого нам стаціонарні точки при знаходженні найбільшого та найменшого значень? Відповідь це питання дає теорема Ферма. З цієї теореми випливає, що якщо функція, що диференціюється, має екстремум (локальний мінімум або локальний максимум) в деякій точці, то ця точка є стаціонарною. Таким чином, функція часто приймає своє найбільше (найменше) значення на проміжку X в одній зі стаціонарних точок цього проміжку.

Також часто найбільше та найменше значення функція може приймати в точках, в яких не існує перша похідна цієї функції, а функція визначена.

Відразу відповімо на одне з найпоширеніших питань на цю тему: "Чи завжди можна визначити найбільше (найменше) значення функції"? Ні не завжди. Іноді межі проміжку X збігаються з межами області визначення функції або інтервал X нескінченний. А деякі функції на нескінченності та на межах області визначення можуть набувати як нескінченно великих так і нескінченно малих значень. У цих випадках нічого не можна сказати про найбільше та найменше значення функції.

Для наочності дамо графічну ілюстрацію. Подивіться малюнки – і багато проясниться.

На відрізку

На першому малюнку функція приймає найбільше (max y) та найменше (min y) значення в стаціонарних точках, що знаходяться всередині відрізка [-6;6].

Розглянемо випадок, зображений другого малюнку. Змінимо відрізок на . У цьому прикладі найменше значення функції досягається в стаціонарній точці, а найбільше - у точці з абсцисою, що відповідає правій межі інтервалу.

На малюнку №3 граничні точки відрізка [-3;2] є абсцисами точок, що відповідають найбільшому та найменшому значенню функції.

На відкритому інтервалі

На четвертому малюнку функція приймає найбільше (max y) і найменше (min y) значення в стаціонарних точках, що знаходяться всередині відкритого інтервалу (-6; 6).

На інтервалі про найбільше значення ніяких висновків зробити не можна.

На нескінченності

У прикладі, представленому на сьомому малюнку, функція приймає найбільше значення (max y) у стаціонарній точці з абсцисою x = 1, а найменше значення (min y) досягається на правій межі інтервалу. На мінус нескінченності значення функції асимптотично наближаються до y=3.

На інтервалі функція не досягає найменшого, ні найбільшого значення. При прагненні до x=2 праворуч значення функції прагнуть мінус нескінченності (пряма x=2 є вертикальною асимптотою), а при прагненні абсциси до плюс нескінченності, значення функції асимптотично наближаються до y=3 . Графічна ілюстрація цього прикладу наведено малюнку №8.

Алгоритм знаходження найбільшого та найменшого значення безперервної функції на відрізку.

Запишемо алгоритм, що дозволяє знаходити найбільше та найменше значення функції на відрізку.

1. Знаходимо область визначення функції та перевіряємо, чи міститься у ній весь відрізок .
2. Знаходимо всі точки, в яких не існує перша похідна і які містяться у відрізку (зазвичай такі точки збігаються у функцій з аргументом під знаком модуля і у статечних функцій з дрібно-раціональним показником). Якщо таких точок немає, переходимо до наступного пункту.
3. Визначаємо всі стаціонарні точки, що потрапляють у відрізок. Для цього, прирівнюємо її до нуля, вирішуємо отримане рівняння і вибираємо відповідне коріння. Якщо стаціонарних точок немає або жодна з них не потрапляє у відрізок, переходимо до наступного пункту.
4. Обчислюємо значення функції у відібраних стаціонарних точках (якщо такі є), у точках, у яких не існує перша похідна (якщо такі є), а також при x=a та x=b .
5. З отриманих значень функції вибираємо найбільше та найменше - вони і будуть шуканими найбільшим та найменшим значеннями функції відповідно.

Розберемо алгоритм при вирішенні прикладу на знаходження найбільшого та найменшого значення функції на відрізку.

приклад.

Знайти найбільше та найменше значення функції

• на відрізку;
• на відрізку [-4;-1].

Рішення.

Областью визначення функції є безліч дійсних чисел, крім нуля, тобто . Обидва відрізки потрапляють у область визначення.

Знаходимо похідну функції по:

Очевидно, похідна функції існує у всіх точках відрізків та [-4;-1] .

Стаціонарні точки визначимо з рівняння. Єдиним дійсним коренем є x=2. Ця стаціонарна точка потрапляє у перший відрізок.

Для першого випадку обчислюємо значення функції на кінцях відрізка і в стаціонарній точці, тобто при x = 1 x = 2 і x = 4 :

Отже, найбільше значення функції досягається при x=1 , а найменше значення - При x = 2 .

Для другого випадку обчислюємо значення функції лише на кінцях відрізка [-4;-1] (оскільки він не містить жодної стаціонарної точки):

Рішення.

Почнемо з області визначення функції. Квадратний тричлен у знаменнику дробу не повинен звертатися до нуля:

Легко перевірити, що всі інтервали з умови завдання належать області визначення функції.

Продиференціюємо функцію:

Очевидно, похідна існує по всій області визначення функції.

Знайдемо стаціонарні точки. Похідна звертається в нуль при . Ця стаціонарна точка потрапляє до інтервалів (-3;1] і (-3;2) .

А тепер можна зіставити отримані у кожному пункті результати із графіком функції. Синіми пунктирними лініями позначені асимптоти.

На цьому можна закінчити із знаходженням найбільшого та найменшого значення функції. Алгоритми, розібрані у цій статті, дозволяють одержати результати при мінімумі дій. Однак буває корисно спочатку визначити проміжки зростання та зменшення функції і тільки після цього робити висновки про найбільше і найменше значення функції на якомусь інтервалі. Це дає більш ясну картину та суворе обґрунтування результатів.

Визначення3 . 3 Нехай - деяка функція, - її область визначення і - деякий (відкритий) інтервал (можливо, з та/або) 7 . Назвемо функцію безперервної на інтерваліякщо безперервна в будь-якій точці, тобто для будь-якого існує (у скороченому записі:

Нехай тепер - (замкнутий) відрізок . Назвемо функцію безперервний на відрізку, якщо безперервна на інтервалі , безперервна справа в точці і безперервна зліва в точці , тобто

приклад3 . 13 Розглянемо функцію (функція Хевісайду) на відрізку , . Тоді безперервна на відрізку (попри те, що у точці вона має розрив першого роду).

Рис.3.15.Графік функції Хевісайду

Аналогічне визначення можна дати і напівінтервалів виду і , включаючи випадки і . Однак можна узагальнити дане визначення на випадок довільного підмножини в такий спосіб. Введемо спочатку поняття індукованоюна бази: нехай - база, всі закінчення якої мають непусті перетину з . Позначимо через і розглянемо безліч усіх. Неважко тоді перевірити, що багато буде базою. Таким чином, для базисів , і , де , і – базиси непроколотих двосторонніх (відповідно лівих, правих) околиць точки (див. їх визначення на початку поточного розділу).

Визначення3 . 4 Назвемо функцію безперервно на знімальному майданчику, якщо

Легко побачити, що тоді при і при це визначення збігається з наведеними вище саме для інтервалу і відрізка.

Нагадаємо, що всі елементарні функції неперервні в усіх точках їх областей визначення і, отже, неперервні на будь-яких інтервалах і відрізках, що лежать в їх областях визначення.

Оскільки неперервність на інтервалі та відрізку визначена поточково, справедлива теорема, яка є прямим наслідком теореми 3.1:

Теорема3 . 5 Нехай і -- функції і -- інтервал або сегмент, що лежить в . Нехай і безперервний протягом . Тоді функції , , безперервний протягом . Якщо додатково на очах у всіх , то функція також постійно ввімкнено .

З цієї теореми, як і з теореми 3.1 – твердження 3.3, випливає таке твердження:

Пропозиція3 . 4 Безліч усі функції, неперервні на інтервалі або сегменті -- це лінійний простір:

Більш складну властивість неперервної функції виражає така теорема.

Теорема3 . 6 (про коріння безперервної функції) Нехай функція неперервна на відрізку , і і -- числа різних знаків. (Будемо для певності вважати, що , а .) Тоді існує хоча б одне таке значення , що (тобто існує хоча б один корінь рівняння ).

Доведення. Розглянемо середину відрізка. Тоді це або, або, або. У першому випадку корінь знайдено: це . У двох інших випадках розглянемо ту частину відрізка, на кінцях якої функція приймає значення різних знаків: в регістр або в регістр. Позначимо виділену половину відрізка через і застосуємо до неї ту саму процедуру: розділимо її на дві половини і , де , і знайдемо . У випадку, якщо знайдено корінь; у випадку, коли ми далі розглядаємо сегмент , у випадку - сегмент і т.д.

3.16 Послідовні ділення відрізка навпіл

Ми отримуємо, що або на якомусь кроці буде знайдено корінь, або буде побудована система вкладених сегментів

у яких кожен наступний відрізок вдвічі менший за попередній. Послідовність неспадна і обмежена зверху (наприклад, числом); тому (за теоремою 2.13) вона має межу. Підпослідовність - незростаючі та обмежені знизу (наприклад, числом ); це означає, що є обмеження. Оскільки довжини відрізків утворюють спадну геометричну прогресію (зі знаменником ), то вони прагнуть до 0, а , тобто . Давайте поставимо це зараз. Тоді

і

оскільки функція неперервна. Проте за побудовою послідовностей і , і , так що за теоремою про граничний перехід у нерівності (теорема 2.7) і, тобто і. Це означає, що , і є коренем рівняння.

приклад3 . 14 Розглянемо функцію на відрізку. Оскільки і є числами різних знаків, функція перетворюється на 0 у певній точці інтервалу. Це означає, що рівняння має корінь.

3.17 Графічне зображення кореня рівняння

Доведена теорема насправді дає нам спосіб знайти корінь, принаймні наближений, із будь-яким ступенем точності, визначеним заздалегідь. Це спосіб поділу відрізка навпіл, описаний у доведенні теореми. З цим та іншими, більш ефективними, методами наближеного знаходження кореня ми познайомимося нижче, після того як вивчимо поняття і властивості похідної.

Зверніть увагу, що теорема не стверджує, що якщо її умови виконуються, то корінь єдиний. Як показано на малюнку нижче, може бути більше одного кореня (на малюнку їх 3).

3.18 Кілька коренів функції, що приймає значення різних знаків на кінцях відрізка

Однак якщо функція монотонно зростає або монотонно спадає на відрізку, на кінцях якого вона приймає значення різних знаків, то корінь єдиний, оскільки строго монотонна функція приймає кожне своє значення рівно в одній точці. , включаючи значення 0.

3.19 Монотонна функція не може мати більше одного кореня

Безпосереднім наслідком теореми про корінь неперервної функції є наступна теорема, яка сама по собі є дуже важливою в математичному аналізі.

Теорема3 . 7 (про проміжне значення неперервної функції) Нехай функція неперервна на відрізку і (для визначеності припустимо, що ). Нехай -- деяке число, що лежить між і . Тоді є такий пункт , що .

3.20 Неперервна функція приймає будь-яке проміжне значення

Доведення. Розглянемо допоміжну функцію , де . Тоді і . Функція, очевидно, неперервна, і за попередньою теоремою існує така точка, що . Але ця рівність означає, що .

Зауважте, що якщо функція не є безперервною, то вона може приймати не всі проміжні значення. Наприклад, функція Хевісайда (див. Приклад 3.13) приймає значення, , але ніде, в тому числі і на інтервалі, не приймає, скажімо, проміжне значення. Справа в тому, що функція Хевісайда має розрив в точці, що лежить точно в інтервалі.

Для подальшого вивчення властивостей неперервних на інтервалі функцій нам знадобиться така тонка властивість системи дійсних чисел (про неї ми вже згадували в розділі 2 у зв’язку з теоремою про границю монотонно зростаючої обмеженої функції): будь-яка множина, обмежена знизу (тобто така, що для всіх і деяких; число називається нижньою граннюмножини ) є точна нижня грань, тобто найбільше з таких чисел, що для всіх . Подібним чином, якщо множина обмежена зверху, то вона обмежена точну верхню грань: це найменша з верхніх граней(Для яких при всіх ).

3.21 Нижня та верхня межі обмеженої множини

Якщо , то існує незростаюча послідовність точок, яка прагне до . Точно так само якщо, то існує невпинна послідовність точок, яка прагне до.

Якщо точка належить множині, то вона є найменшим елементом цієї множини: ; так само якщо , то.

Крім того, для подальшого нам знадобиться наступне

Лемма3 . 1 Нехай -- неперервна функція на відрізку , і безліч тих точок , в яких (або , або ) не порожньо. Тоді в надлишку є найменше значення , таке що при всіх .

3.22 Найменший аргумент, при якому функція приймає задане значення

Доведення. Оскільки це обмежена множина (є частиною відрізка), вона має нижню грань. Тоді існує незростаюча послідовність , , така, що для . При цьому, за визначенням множини. Тому, переходячи до межі, отримуємо, з одного боку,

а з іншого боку, внаслідок безперервності функції ,

Отже, , отже точка належить безлічі і .

У випадку, коли множина визначається нерівністю , маємо для всіх і за теоремою про граничний перехід у нерівності маємо

звідки , Що означає, що і . Так само у разі нерівності перехід до межі в нерівності дає

звідки, і.

Теорема3 . 8 (Про обмеженість безперервної функції) Нехай функція неперервна на відрізку . Тоді обмежується , тобто існує така постійна , що при всіх .

Рис.3.23. Безперервна на відрізку функція обмежена

Доведення. Припустимо зворотне: нехай не обмежена, наприклад, зверху. Тоді всі множини , , , не порожні. По попередній лемі у кожному з цих множин є найменше значення , . Покажемо, що

Справді, . Якщо якась точка з , наприклад , лежить між і , то

тобто - проміжне значення між і. Отже, за теоремою про проміжне значення безперервної функції існує точка , така що , та . Але, всупереч припущенню, що - найменше значення множини. З цього випливає, що для всіх .

Таким же чином, далі доведено, що для всіх , для всіх і т.д. Отже, є зростаюча послідовність, обмежена зверху числом . Тому він існує. З неперервності функції випливає, що існує , але на , тому обмежень немає. Отримане протиріччя доводить, що функція обмежена зверху.

Подібним чином доводиться його обмеженість знизу, з чого випливає твердження теореми.

Очевидно, що неможливо послабити умови теореми: якщо функція не є неперервною, то вона не повинна бути обмеженою на інтервалі (наведемо як приклад функцію

на відрізку. Ця функція не обмежена на інтервалі, оскільки на має точку розриву другого роду, таку, що при . Замінити відрізок в умові теореми інтервалом або півінтервалом також не можна: для прикладу розглянемо ту ж функцію на півінтервалі. Функція є неперервною на цьому півінтервалі, але необмеженою внаслідок того, що при .

Пошук найкращих констант, які можна використовувати для обмеження функції зверху і знизу на даному інтервалі, природно, призводить нас до проблеми знаходження мінімуму і максимуму неперервної функції на цьому інтервалі. Можливість вирішення цієї задачі описує наступна теорема.

Теорема3 . 9 (про досягнення екстремуму неперервною функцією) Нехай функція неперервна на відрізку . Тоді є крапка , така що при всіх (тобто -- мінімальний бал: ), і тут є сенс , така що при всіх (тобто -- максимальний бал: ). Іншими словами, мінімум і максимум 8 значення неперервної функції на відрізку існують і досягаються в деяких точках і цей сегмент.

3.24 Неперервна на відрізку функція досягає максимуму і мінімуму

Доведення. Оскільки згідно з попередньою теоремою функція обмежена вище, то існує точна верхня межа значень функції за -- числом . Таким чином, множини , ,..., ,..., не порожні і за попередньою лемою містять найменші значення: , . Вони не спадають (це твердження доводиться точно так само, як і в попередній теоремі):

і обмежені зверху . Отже, згідно з теоремою про границю монотонної обмеженої послідовності існує межа Оскільки , то й

за теоремою про граничний перехід у нерівності, тобто . Але з усіма, в тому числі. Звідси виходить, що , тобто максимум функції досягається в точці .

Подібним чином доводиться існування точки мінімуму.

У цій теоремі, як і в попередній, неможливо послабити умови: якщо функція неперервна, то вона може не досягти максимального або мінімального значення на відрізку, навіть якщо він обмежений. Для прикладу візьмемо функцію

на відрізку. Ця функція обмежена на інтервалі (очевидно) і , однак він не приймає значення 1 у жодній точці відрізка (зауважте, що , а не 1). Справа в тому, що ця функція має розрив першого роду в точці , так що в межі не дорівнює значенню функції в точці 0. Крім того, неперервна функція, визначена на інтервалі або іншій множині, яка не замкнутий відрізок (на півінтервалі, півосі) також може не приймати екстремальних значень. Як приклад розглянемо функцію на інтервалі . Очевидно, що функція неперервна і що і , однак функція не приймає ні значення 0, ні значення 1 в жодній точці інтервалу . Розглянемо також функцію на півосі. Ця функція неперервна на , зростає, приймає своє мінімальне значення 0 у точці , але не приймає максимального значення в жодній точці (хоча вона обмежена зверху числом і

Визначення. Якщо функція f(x) визначено на проміжку [ a, b], неперервна в кожній точці інтервалу ( a, b), в точці aбезперервний праворуч, у точці bбезперервна зліва, то кажуть, що функція f(x) неперервна на відрізку [a, b].

Іншими словами, функція f(x) неперервна на проміжку [ a, b], якщо виконано три умови:

1) "x 0 Î( a, b): f(x) = f(x 0);

2) f(x) = f(a);

3) f(x) = f(b).

Для неперервних на інтервалі функцій розглянемо деякі властивості, які сформулюємо у вигляді наступних теорем, не проводячи доведення.

Теорема 1. Якщо функція f(x) неперервна на проміжку [ a, b], то він досягає свого мінімального і максимального значень на цьому відрізку.

Ця теорема стверджує (рис. 1.15), що у відрізку [ a, b] є такий пункт x 1 це f(x 1) £ f(x) для будь-якого xвід [ a, b] і в цьому є сенс x 2 (x 2 О[ a, b]) такий як " xÎ[ a, b] (f(x 2)³ f(x)).

Значення f(x 1) є найбільшим для цієї функції на [ a, b], а f(x 2) – найменший. Позначимо: f(x 1) = M, f(x 2) =m. Оскільки для f(x) виконується нерівність: " xÎ[ a, b] m£ f(x) £ M, Отримуємо наступне слідство з теореми 1.

Слідство. Якщо функція f(x) безперервна на відрізку, то вона обмежена на цьому відрізку.

Теорема 2. Якщо функція f(x) неперервна на проміжку [ а,б] і на кінцях відрізка приймає значення різних знаків, то є така внутрішня точка x 0 сегмент [ a, b], у якій функція звертається до 0, тобто. $ x 0 Î ( a, b) (f(x 0) = 0).

Ця теорема стверджує, що графік функції y = f(x), неперервна на проміжку [ a, b], перетинає вісь Oxхоча б один раз, якщо значення f(a) та f(b) мають протилежні знаки. Отже, (рис. 1.16) f(a) > 0, f(b) < 0 и функция f(x) звертається до 0 у точках x 1 , x 2 , x 3 .

Теорема 3. Нехай функція f(x) неперервна на проміжку [ a, b], f(a) = A, f(b) = Bі A¹ B. (Рис. 1.17). Тоді для будь-якого числа C, укладеного між числами Aі B, знайдеться така внутрішня точка x 0 сегмент [ a, b], що f(x 0) = C.

Слідство. Якщо функція f(x) неперервна на проміжку [ a, b], m– найменше значення f(x), M– найбільше значення функції f(x) на відрізку [ a, b], тоді функція приймає (принаймні один раз) будь-яке значення m, укладений між mі M, а тому відрізок [ m, M] — множина всіх значень функції f(x) на відрізку [ a, b].

Зауважте, що якщо функція неперервна на інтервалі ( a, b) або має на відрізку [ a, b] точки розриву, то теореми 1, 2, 3 для такої функції перестають бути істинними.

На закінчення розглянемо теорему про існування оберненої функції.

Теорема 4. Нехай f(x) безперервна на проміжку X, збільшується (або зменшується) на Xі має діапазон значень Y. Тоді для функції y = f(x) існує обернена функція x= j(y), визначеному на інтервалі Y, безперервний і зростаючий (або спадаючий) на Yз безліччю значень X.

Зауваження. Нехай функція x= j(y) є оберненою функцією f(x). Оскільки аргумент зазвичай позначається x, а функцію через y, то запишемо обернену функцію у вигляді y =j(x).

Приклад 1. Функція y = x 2 (рис. 1.8, а) на множині X= }