MGA KATANGIAN NG MGA TUNGKULIN NA PATULOY SA ISANG PANAYAM

Isaalang-alang natin ang ilang mga katangian ng mga function na tuloy-tuloy sa isang pagitan. Ipinakita namin ang mga katangiang ito nang walang patunay.

Function y = f(x) tinawag tuloy-tuloy sa segment [a, b], kung ito ay tuloy-tuloy sa lahat ng panloob na punto ng segment na ito, at sa mga dulo nito, i.e. sa mga punto a At b, ay tuloy-tuloy sa kanan at kaliwa, ayon sa pagkakabanggit.

Teorama 1. Isang function na tuloy-tuloy sa pagitan [ a, b], hindi bababa sa isang punto ng segment na ito ay tumatagal ng pinakamalaking halaga at hindi bababa sa isang punto ang pinakamaliit.

Ang theorem ay nagsasaad na kung ang isang function y = f(x) ay tuloy-tuloy sa pagitan [ a, b], pagkatapos ay mayroong kahit isang punto x 1 Î [ a, b] na ang halaga ng function f(x) sa puntong ito ay magiging pinakamalaki sa lahat ng mga halaga nito sa segment na ito: f(x 1) ≥ f(x). Katulad nito, may ganoong punto x 2, kung saan ang value ng function ang magiging pinakamaliit sa lahat ng value sa segment: f(x 1) ≤ f(x).

Ito ay malinaw na maaaring mayroong ilang mga tulad na mga punto, halimbawa, ang figure ay nagpapakita na ang function f(x) kumukuha ng pinakamaliit na halaga sa dalawang punto x 2 At x 2 ".

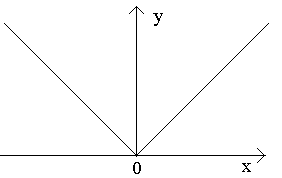
Magkomento. Ang pahayag ng theorem ay maaaring maging mali kung isasaalang-alang natin ang halaga ng function sa pagitan ( a, b). Sa katunayan, kung isasaalang-alang natin ang pag-andar y = x sa (0, 2), pagkatapos ito ay tuloy-tuloy sa agwat na ito, ngunit hindi maabot ang alinman sa pinakamalaki o pinakamaliit na halaga dito: naabot nito ang mga halagang ito sa mga dulo ng agwat, ngunit ang mga dulo ay hindi nabibilang sa aming domain.

Gayundin, ang teorama ay tumigil na maging totoo para sa mga di-tuloy na pag-andar. Magbigay ng halimbawa.

Bunga. Kung ang function f(x) ay tuloy-tuloy sa [ a, b], kung gayon ito ay limitado sa segment na ito.

Teorama 2. Hayaan ang function y = f(x) ay tuloy-tuloy sa pagitan [ a, b] at sa mga dulo ng segment na ito ay kumukuha ng mga halaga ng iba't ibang mga palatandaan, pagkatapos ay mayroong hindi bababa sa isang punto sa loob ng segment x = C, kung saan ang function ay napupunta sa zero: f(C)= 0, kung saan a< C< b

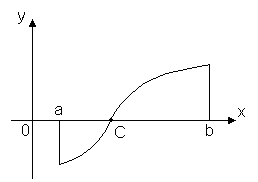
Ang theorem na ito ay may isang simpleng geometric na kahulugan: kung ang mga punto ng graph ng isang tuluy-tuloy na function y = f(x), naaayon sa mga dulo ng segment [ a, b] nakahiga sa magkabilang panig ng axis baka, pagkatapos ay i-intersect ng graph na ito ang axis kahit man lang isang punto ng segment baka. Maaaring walang ganitong katangian ang mga hindi tuluy-tuloy na function.

Ang teorama na ito ay umamin sa sumusunod na paglalahat.

Theorem 3 (intermediate value theorem). Hayaan ang function y = f(x) ay tuloy-tuloy sa pagitan [ a, b] At f(a) = A, f(b) = B. Pagkatapos ay para sa anumang numero C, nagtapos sa pagitan ng A At B, may ganoong punto sa loob ng segment na ito CÎ [ a, b], Ano f(c) = C.

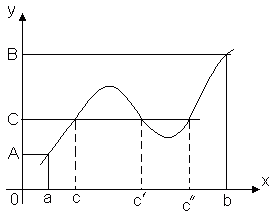
Ang teorama na ito ay geometrically obvious. Isaalang-alang ang graph ng function y = f(x). Hayaan f(a) = A, f(b) = B. Pagkatapos ng anumang tuwid na linya y = C, Saan C– anumang numero sa pagitan A At B, ay mag-intersect sa graph ng function kahit man lang sa isang punto. Ang abscissa ng intersection point ay ang halagang iyon x = C, Kung saan f(c) = C.

Kaya, ang isang tuluy-tuloy na pag-andar, na lumilipat mula sa isang halaga patungo sa isa pa, ay kinakailangang dumaan sa lahat ng mga intermediate na halaga. Sa partikular:

Bunga. Kung ang function y = f(x) ay tuluy-tuloy sa isang tiyak na pagitan at kumukuha ng pinakamalaki at pinakamaliit na halaga, pagkatapos ay sa pagitan na ito ay tumatagal ng kahit isang beses ang anumang halaga na nasa pagitan ng pinakamaliit at pinakamalaking halaga nito.

DERIVATIVE AT MGA APLIKASYON NITO. KAHULUGAN NG DERIVATIVE

Magkaroon tayo ng ilang function y=f(x), tinukoy sa ilang pagitan. Para sa bawat halaga ng argumento x mula sa pagitan na ito ang function y=f(x) may tiyak na kahulugan.

Isaalang-alang ang dalawang halaga ng argumento: inisyal x 0 at bago x.

Pagkakaiba x–x 0 ang tinatawag sa pamamagitan ng pagdaragdag ng argumento x sa punto x 0 at ipinapahiwatig Δx. kaya, Δx = x – x 0 (ang pagtaas ng argumento ay maaaring maging positibo o negatibo). Mula sa pagkakapantay-pantay na ito ay sinusundan iyon x=x 0 +Δx, ibig sabihin. ang paunang halaga ng variable ay nakatanggap ng ilang pagtaas. Pagkatapos, kung sa punto x 0 ang halaga ng function noon f(x 0 ), pagkatapos ay sa isang bagong punto x ang function ay kukuha ng halaga f(x) = f(x 0 +Δx).

Pagkakaiba y–y 0 = f(x) – f(x 0 ) tinawag pagtaas ng function y = f(x) sa punto x 0 at ipinahiwatig ng simbolo Δy. kaya,

Karaniwan ang paunang halaga ng argumento x 0 ay itinuturing na naayos, at ang bagong halaga x– variable. Pagkatapos y 0 = f(x 0 ) lumalabas na pare-pareho, at y = f(x)– variable. Mga dagdag Δy At Δx magiging mga variable din at ang formula (1) ay nagpapakita na Dy ay isang function ng isang variable Δx.

Gawin natin ang ratio ng increment ng function sa increment ng argument

Hanapin natin ang limitasyon ng ratio na ito sa Δx→0. Kung umiiral ang limitasyong ito, kung gayon ito ay tinatawag na derivative ng function na ito f(x) sa punto x 0 at tukuyin f "(x 0). Kaya,

Derivative function na ito y = f(x) sa punto x Ang 0 ay tinatawag na limitasyon ng ratio ng pagtaas ng function na Δ y sa argumentong pagtaas Δ x, kapag ang huli ay arbitraryong nagiging zero.

Tandaan na para sa parehong function ang derivative sa iba't ibang mga punto x maaaring tumagal sa iba't ibang mga halaga, i.e. ang derivative ay maaaring ituring bilang isang function ng argumento x. Ang function na ito ay itinalaga f "(x)

Ang derivative ay tinutukoy ng mga simbolo f "(x), y", . Ang tiyak na halaga ng derivative sa x = a ipinapahiwatig ng f "(a) o y "| x=a.

Ang operasyon ng paghahanap ng derivative ng isang function f(x) ay tinatawag na pagkita ng kaibhan ng function na ito.

Upang direktang mahanap ang derivative ayon sa kahulugan, maaari mong gamitin ang sumusunod: pamantayan:

Mga halimbawa.

MECHANICAL SENSE OF DERIVATIVE

Ito ay kilala mula sa pisika na ang batas ng unipormeng paggalaw ay may anyo s = v t, Saan s– ang landas ay naglakbay patungo sa sandali ng panahon t, v- bilis ng pare-parehong paggalaw.

Gayunpaman, dahil Karamihan sa mga paggalaw na nagaganap sa kalikasan ay hindi pantay, pagkatapos ay sa pangkalahatan ang bilis, at, dahil dito, ang distansya. s ay depende sa oras t, ibig sabihin. magiging function ng oras.

Kaya, hayaan ang isang materyal na punto na lumipat sa isang tuwid na linya sa isang direksyon ayon sa batas s=s(t).

Markahan natin ang isang tiyak na punto ng oras t 0 . Sa puntong ito ang punto ay lumipas na sa landas s=s(t 0 ). Tukuyin natin ang bilis v materyal na punto sa isang sandali sa oras t 0 .

Upang gawin ito, isaalang-alang natin ang ilang iba pang punto sa oras t 0 + Δ t. Ito ay tumutugma sa nilakbay na landas s =s(t 0 + Δ t). Pagkatapos sa isang yugto ng panahon Δ t ang punto ay naglakbay sa landas na Δs =s(t 0 + Δ t)–s(t).

Isaalang-alang natin ang saloobin. Ito ay tinatawag na average na bilis sa pagitan ng oras Δ t. Ang average na bilis ay hindi maaaring tumpak na makilala ang bilis ng paggalaw ng isang punto sa sandaling ito t 0 (dahil hindi pantay ang paggalaw). Upang mas tumpak na maipahayag ang totoong bilis na ito gamit ang average na bilis, kailangan mong kumuha ng mas maikling panahon Δ t.

Kaya, ang bilis ng paggalaw sa isang naibigay na sandali sa oras t 0 (madaliang bilis) ay ang limitasyon ng average na bilis sa pagitan mula sa t 0 hanggang t 0 +Δ t, kapag Δ t→0:

,

mga. hindi pantay na bilis ito ang derivative ng distansyang nilakbay patungkol sa oras.

HEOMETRICAL MEANING NG DERIVATIVE

Ipakilala muna natin ang kahulugan ng isang tangent sa isang kurba sa isang naibigay na punto.

Magkaroon tayo ng isang kurba at isang nakapirming punto dito M 0(tingnan ang figure) Isaalang-alang ang isa pang punto M curve na ito at gumuhit ng secant M 0 M. Kung ang punto M nagsisimulang gumalaw kasama ang kurba, at ang punto M 0 nananatiling hindi gumagalaw, pagkatapos ay nagbabago ang secant ng posisyon nito. Kung, na may walang limitasyong pagtatantya ng punto M kasama ang isang kurba sa isang punto M 0 sa anumang panig ang secant ay may posibilidad na sumakop sa posisyon ng isang tiyak na tuwid na linya M 0 T, pagkatapos ay diretso M 0 T tinatawag ang padaplis sa kurba sa isang naibigay na punto M 0.

yun., padaplis sa kurba sa isang naibigay na punto M 0 tinatawag na limitasyon na posisyon ng secant M 0 M kapag point M tends along the curve to a point M 0.

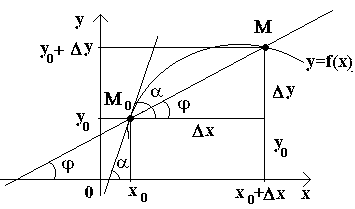
Isaalang-alang natin ngayon ang tuluy-tuloy na pag-andar y=f(x) at ang curve na naaayon sa function na ito. Sa ilang halaga X 0 function ay tumatagal ng halaga y 0 =f(x 0). Ang mga halagang ito x 0 at y 0 sa curve ay tumutugma sa isang punto M 0 (x 0 ; y 0). Ibigay natin ang argumento x 0 pagtaas Δ X. Ang bagong value ng argument ay tumutugma sa incremented value ng function y 0 +Δ y=f(x 0 –Δ x). Nakukuha namin ang punto M(x 0+Δ x; y 0+Δ y). Gumuhit tayo ng secant M 0 M at tukuyin sa pamamagitan ng φ ang anggulo na nabuo ng isang secant na may positibong direksyon ng axis baka. Gumawa tayo ng isang relasyon at pansinin na .

Kung ngayon Δ x→0, pagkatapos ay dahil sa pagpapatuloy ng function na Δ sa→0, at samakatuwid ang punto M, gumagalaw sa isang kurba, lumalapit sa puntong walang limitasyon M 0. Tapos yung secant M 0 M ay may posibilidad na kunin ang posisyon ng isang padaplis sa kurba sa punto M 0, at ang anggulo φ→α sa Δ x→0, kung saan ang α ay tumutukoy sa anggulo sa pagitan ng tangent at ng positibong direksyon ng axis baka. Dahil ang function na tan φ ay patuloy na nakasalalay sa φ para sa φ≠π/2, kung gayon para sa φ→α tan φ → tan α at, samakatuwid, ang slope ng tangent ay magiging:

mga. f "(x)= tg α .

Kaya, geometrically y "(x 0) kumakatawan sa slope ng tangent sa graph ng function na ito sa punto x 0, ibig sabihin. para sa isang ibinigay na halaga ng argumento x, ang derivative ay katumbas ng tangent ng anggulo na nabuo ng tangent sa graph ng function f(x) sa angkop na punto M 0 (x; y) na may positibong direksyon ng axis baka.

Halimbawa. Hanapin ang slope ng tangent sa curve y = x 2 sa punto M(-1; 1).

Nakita na natin kanina na ( x 2)" = 2X. Ngunit ang angular coefficient ng tangent sa curve ay tan α = y"| x=-1 = – 2.

PAGKAKAIBA NG MGA FUNCTION. PAGPAPATULOY NG NAIIBA NA FUNCTION

Function y=f(x) tinawag naiba-iba sa isang punto x 0 kung mayroon itong tiyak na derivative sa puntong ito, i.e. kung ang limitasyon ng relasyon ay umiiral at may hangganan.

Kung ang isang function ay naiba sa bawat punto ng isang partikular na segment [ A; b] o pagitan ( A; b), pagkatapos ay sinasabi nila na siya naiba-iba sa segment [ A; b] o, ayon sa pagkakabanggit, sa pagitan ( A; b).

Ang sumusunod na theorem ay wasto, na nagtatatag ng koneksyon sa pagitan ng naiba at tuluy-tuloy na mga pag-andar.

Teorama. Kung ang function y=f(x) naiba sa isang punto x 0, pagkatapos ito ay tuloy-tuloy sa puntong ito.

Kaya, mula sa pagkakaiba-iba ng isang function, ang pagpapatuloy nito ay sumusunod.

Patunay. Kung , Iyon

,

kung saan ang α ay isang infinitesimal na dami, i.e. isang dami na may posibilidad na zero bilang Δ x→0. Ngunit pagkatapos

Δ y=f "(x 0) Δ x+αΔ x=> Δ y→0 sa Δ x→0, ibig sabihin. f(x) – f(x 0)→0 sa x→x 0 , na nangangahulugan na ang function f(x) tuloy-tuloy sa isang punto x 0 . Q.E.D.

Kaya, hindi maaaring magkaroon ng derivative ang function sa mga discontinuity point. Ang kabaligtaran ay hindi totoo: may mga tuluy-tuloy na pag-andar na hindi naiiba sa ilang mga punto (iyon ay, walang derivative sa mga puntong ito).

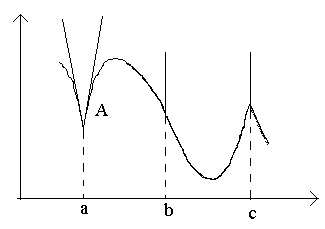
Isaalang-alang ang mga punto sa figure a, b, c.

Sa punto a sa Δ x→0 ang ratio ay walang limitasyon (dahil ang mga one-sided na limitasyon ay iba para sa Δ x→0–0 at Δ x→0+0). Sa punto A graph walang tinukoy na tangent, ngunit mayroong dalawang magkaibang one-way na tangent na may mga slope Upang 1 at Upang 2. Ang ganitong uri ng punto ay tinatawag na corner point.

Sa punto b sa Δ x Ang →0 ratio ay isang pare-parehong tanda na walang katapusang malaking dami. Ang function ay may walang katapusang derivative. Sa puntong ito ang graph ay may patayong padaplis. Uri ng punto - "inflection point" ng isang patayong padaplis.

Sa punto c Ang mga one-sided derivatives ay walang katapusang malalaking dami ng iba't ibang mga palatandaan. Sa puntong ito ang graph ay may dalawang pinagsamang vertical tangent. Uri – “return point” na may vertical tangent – ​​isang espesyal na case ng isang corner point.

Ipinapakita ng mga figure sa ibaba kung saan maaaring maabot ng function ang pinakamaliit at pinakamalaking halaga nito. Sa kaliwang figure, ang pinakamaliit at pinakamalaking halaga ay naayos sa mga punto ng lokal na minimum at maximum ng function. Sa kanang larawan - sa mga dulo ng segment.

Kung ang function y = f(x) ay tuloy-tuloy sa pagitan [ a, b] , pagkatapos ay umabot ito sa segment na ito hindi bababa sa At pinakamataas na halaga . Ito, tulad ng nabanggit na, ay maaaring mangyari alinman sa matinding puntos, o sa mga dulo ng segment. Samakatuwid, upang mahanap hindi bababa sa At ang pinakamalaking halaga ng function , tuloy-tuloy sa pagitan [ a, b] , kailangan mong kalkulahin ang mga halaga nito sa lahat kritikal na puntos at sa mga dulo ng segment, at pagkatapos ay piliin ang pinakamaliit at pinakamalaki mula sa kanila.

Hayaan, halimbawa, gusto mong matukoy ang pinakamalaking halaga ng function f(x) sa segment [ a, b] . Upang gawin ito, kailangan mong hanapin ang lahat ng mga kritikal na punto nito na nakalagay sa [ a, b] .

Kritikal na punto tinatawag ang punto kung saan tinukoy ang function, at siya derivative katumbas ng zero o wala. Pagkatapos ay dapat mong kalkulahin ang mga halaga ng pag-andar sa mga kritikal na punto. At sa wakas, dapat ihambing ng isa ang mga halaga ng pag-andar sa mga kritikal na punto at sa mga dulo ng segment ( f(a) At f(b)). Ang pinakamalaki sa mga bilang na ito ay magiging ang pinakamalaking halaga ng function sa segment [a, b] .

Mga problema sa paghahanap pinakamaliit na halaga ng function .

Hinahanap namin ang pinakamaliit at pinakamalaking halaga ng function nang magkasama

Halimbawa 1. Hanapin ang pinakamaliit at pinakamalaking halaga ng isang function sa segment [-1, 2] .

Solusyon. Hanapin ang derivative ng function na ito. I-equate natin ang derivative sa zero () at makakuha ng dalawang kritikal na puntos: at . Upang mahanap ang pinakamaliit at pinakamalaking halaga ng isang function sa isang partikular na segment, sapat na upang kalkulahin ang mga halaga nito sa mga dulo ng segment at sa punto, dahil ang punto ay hindi kabilang sa segment [-1, 2]. Ang mga halaga ng function na ito ay: , , . Sinusundan nito iyon pinakamaliit na halaga ng function(ipinahiwatig sa pula sa graph sa ibaba), katumbas ng -7, ay nakakamit sa kanang dulo ng segment - sa punto , at pinakadakila(pula din sa graph), katumbas ng 9, - sa kritikal na punto.

Kung ang isang function ay tuluy-tuloy sa isang tiyak na agwat at ang agwat na ito ay hindi isang segment (ngunit, halimbawa, isang agwat; ang pagkakaiba sa pagitan ng isang agwat at isang segment: ang mga hangganan ng mga punto ng agwat ay hindi kasama sa agwat, ngunit ang Ang mga hangganan ng mga punto ng segment ay kasama sa segment), pagkatapos ay kabilang sa mga halaga ng pag-andar ay maaaring walang pinakamaliit at pinakamalaki. Kaya, halimbawa, ang function na ipinapakita sa figure sa ibaba ay tuloy-tuloy sa ]-∞, +∞[ at walang pinakamalaking halaga.

Gayunpaman, para sa anumang agwat (sarado, bukas o walang katapusan), ang sumusunod na katangian ng tuluy-tuloy na pag-andar ay totoo.

Para sa self-checking sa panahon ng mga kalkulasyon, maaari mong gamitin online na derivative calculator .

Halimbawa 4. Hanapin ang pinakamaliit at pinakamalaking halaga ng isang function sa segment [-1, 3] .

Solusyon. Nakita namin ang derivative ng function na ito bilang derivative ng quotient:

.

Tinutumbas namin ang derivative sa zero, na nagbibigay sa amin ng isang kritikal na punto: . Ito ay kabilang sa segment [-1, 3] . Upang mahanap ang pinakamaliit at pinakamalaking halaga ng isang function sa isang partikular na segment, makikita namin ang mga halaga nito sa mga dulo ng segment at sa natagpuang kritikal na punto:

Ihambing natin ang mga halagang ito. Konklusyon: katumbas ng -5/13, sa punto at pinakamataas na halaga katumbas ng 1 sa punto .

Patuloy kaming naghahanap ng pinakamaliit at pinakamalaking halaga ng pag-andar nang magkasama

May mga guro na, sa paksa ng paghahanap ng pinakamaliit at pinakamalaking halaga ng isang function, ay hindi nagbibigay sa mga mag-aaral ng mga halimbawa upang malutas na mas kumplikado kaysa sa mga napag-usapan, iyon ay, ang mga kung saan ang function ay isang polynomial o isang fraction, ang numerator at denominator nito ay mga polynomial. Ngunit hindi namin lilimitahan ang ating sarili sa gayong mga halimbawa, dahil sa mga guro ay may mga gustong pilitin ang mga mag-aaral na mag-isip nang buo (ang talahanayan ng mga derivatives). Samakatuwid, gagamitin ang logarithm at trigonometric function.

Halimbawa 8. Hanapin ang pinakamaliit at pinakamalaking halaga ng isang function sa segment .

Solusyon. Nakikita namin ang derivative ng function na ito bilang derivative ng produkto :

Tinutumbas namin ang derivative sa zero, na nagbibigay ng isang kritikal na punto: . Ito ay kabilang sa segment. Upang mahanap ang pinakamaliit at pinakamalaking halaga ng isang function sa isang partikular na segment, makikita namin ang mga halaga nito sa mga dulo ng segment at sa natagpuang kritikal na punto:

Resulta ng lahat ng aksyon: ang function ay umabot sa pinakamababang halaga nito, katumbas ng 0, sa punto at sa punto at pinakamataas na halaga, katumbas e², sa punto.

Para sa self-checking sa panahon ng mga kalkulasyon, maaari mong gamitin online na derivative calculator .

Halimbawa 9. Hanapin ang pinakamaliit at pinakamalaking halaga ng isang function sa segment .

Solusyon. Hanapin ang derivative ng function na ito:

Tinutumbas namin ang derivative sa zero:

Ang tanging kritikal na punto ay kabilang sa segment. Upang mahanap ang pinakamaliit at pinakamalaking halaga ng isang function sa isang partikular na segment, makikita namin ang mga halaga nito sa mga dulo ng segment at sa natagpuang kritikal na punto:

Konklusyon: ang function ay umabot sa pinakamababang halaga nito, katumbas ng , sa punto at pinakamataas na halaga, pantay , sa punto .

Sa mga inilapat na matinding problema, ang paghahanap ng pinakamaliit (maximum) na mga halaga ng isang function, bilang panuntunan, ay bumababa sa paghahanap ng pinakamababa (maximum). Ngunit hindi ang mga minimum o maximum mismo ang mas praktikal na interes, ngunit ang mga halaga ng argumento kung saan nakamit ang mga ito. Kapag nilulutas ang mga inilapat na problema, isang karagdagang kahirapan ang lumitaw - ang pagbuo ng mga function na naglalarawan sa kababalaghan o proseso na isinasaalang-alang.

Halimbawa 10. Ang isang tangke na may kapasidad na 4, na may hugis ng parallelepiped na may parisukat na base at bukas sa itaas, ay dapat na tinned. Anong sukat ang dapat na tangke upang ang hindi bababa sa dami ng materyal ay ginagamit upang takpan ito?

Solusyon. Hayaan x- gilid ng base, h- taas ng tangke, S- ang ibabaw nito na walang takip, V- ang dami nito. Ang ibabaw na lugar ng tangke ay ipinahayag ng formula, i.e. ay isang function ng dalawang variable. Upang ipahayag S bilang isang function ng isang variable, ginagamit namin ang katotohanan na , mula sa kung saan . Pagpapalit sa nahanap na expression h sa pormula para sa S:

Suriin natin ang function na ito hanggang sa sukdulan nito. Ito ay tinukoy at naiba-iba sa lahat ng dako sa ]0, +∞[ , at

.

Tinutumbas namin ang derivative sa zero () at hanapin ang kritikal na punto. Bilang karagdagan, kapag ang derivative ay hindi umiiral, ngunit ang halagang ito ay hindi kasama sa domain ng kahulugan at samakatuwid ay hindi maaaring maging isang extremum point. Kaya, ito lamang ang kritikal na punto. Suriin natin ito para sa pagkakaroon ng extremum gamit ang pangalawang sapat na tanda. Hanapin natin ang pangalawang derivative. Kapag ang pangalawang derivative ay mas malaki sa zero (). Nangangahulugan ito na kapag ang function ay umabot sa isang minimum . Simula noon Ang minimum ay ang tanging extremum ng function na ito, ito ang pinakamaliit na halaga nito. Kaya, ang gilid ng base ng tangke ay dapat na 2 m, at ang taas nito ay dapat na .

Para sa self-checking sa panahon ng mga kalkulasyon, maaari mong gamitin

Mula sa praktikal na pananaw, ang pinakamalaking interes ay ang paggamit ng derivative upang mahanap ang pinakamalaki at pinakamaliit na halaga ng isang function. Ano ang konektado dito? Pag-maximize ng kita, pagliit ng mga gastos, pagtukoy ng pinakamainam na pagkarga ng kagamitan... Sa madaling salita, sa maraming lugar ng buhay kailangan nating lutasin ang mga problema sa pag-optimize ng ilang mga parameter. At ito ang mga gawain ng paghahanap ng pinakamalaki at pinakamaliit na halaga ng isang function.

Dapat tandaan na ang pinakamalaki at pinakamaliit na halaga ng isang function ay karaniwang hinahanap sa isang tiyak na pagitan X, na alinman sa buong domain ng function o bahagi ng domain ng kahulugan. Ang interval X mismo ay maaaring isang segment, isang bukas na agwat , isang walang katapusang pagitan.

Sa artikulong ito ay pag-uusapan natin ang tungkol sa paghahanap ng pinakamalaki at pinakamaliit na halaga ng isang tahasang tinukoy na function ng isang variable y=f(x) .

Pag-navigate sa pahina.

Ang pinakamalaki at pinakamaliit na halaga ng isang function - mga kahulugan, mga guhit.

Tingnan natin sa madaling sabi ang mga pangunahing kahulugan.

Ang pinakamalaking halaga ng function na para sa sinuman totoo ang hindi pagkakapantay-pantay.

Ang pinakamaliit na halaga ng function y=f(x) sa pagitan ng X ay tinatawag na ganoong halaga na para sa sinuman totoo ang hindi pagkakapantay-pantay.

Ang mga kahulugang ito ay madaling maunawaan: ang pinakamalaking (pinakamaliit) na halaga ng isang function ay ang pinakamalaking (pinakamaliit) na tinatanggap na halaga sa pagitan na isinasaalang-alang sa abscissa.

Mga nakatigil na puntos– ito ang mga halaga ng argumento kung saan ang derivative ng function ay nagiging zero.

Bakit kailangan natin ng mga nakatigil na puntos kapag hinahanap ang pinakamalaki at pinakamaliit na halaga? Ang sagot sa tanong na ito ay ibinigay ng Fermat's theorem. Mula sa theorem na ito ay sumusunod na kung ang isang differentiable function ay may extremum (lokal na minimum o lokal na maximum) sa isang punto, kung gayon ang puntong ito ay nakatigil. Kaya, madalas na kinukuha ng function ang pinakamalaking (pinakamaliit) na halaga nito sa pagitan ng X sa isa sa mga nakatigil na punto mula sa agwat na ito.

Gayundin, ang isang function ay kadalasang maaaring tumagal sa pinakamalaki at pinakamaliit na halaga nito sa mga punto kung saan ang unang derivative ng function na ito ay hindi umiiral, at ang function mismo ay tinukoy.

Agad nating sagutin ang isa sa mga pinakakaraniwang tanong sa paksang ito: "Palaging posible bang matukoy ang pinakamalaking (pinakamaliit) na halaga ng isang function"? Hindi hindi palagi. Minsan ang mga hangganan ng interval X ay nag-tutugma sa mga hangganan ng domain ng kahulugan ng function, o ang interval X ay walang katapusan. At ang ilang mga pag-andar sa infinity at sa mga hangganan ng domain ng kahulugan ay maaaring tumagal sa parehong walang katapusan na malaki at walang katapusang maliit na halaga. Sa mga kasong ito, walang masasabi tungkol sa pinakamalaki at pinakamaliit na halaga ng function.

Para sa kalinawan, magbibigay kami ng isang graphic na paglalarawan. Tingnan ang mga larawan at marami ang magiging mas malinaw.

Sa segment

Sa unang figure, ang function ay tumatagal ng pinakamalaking (max y) at pinakamaliit (min y) na mga halaga sa mga nakatigil na punto na matatagpuan sa loob ng segment [-6;6].

Isaalang-alang ang kaso na inilalarawan sa pangalawang figure. Baguhin natin ang segment sa . Sa halimbawang ito, ang pinakamaliit na halaga ng function ay nakakamit sa isang nakatigil na punto, at ang pinakamalaking sa punto na may abscissa na tumutugma sa kanang hangganan ng pagitan.

Sa Figure 3, ang mga boundary point ng segment [-3;2] ay ang abscissas ng mga puntos na tumutugma sa pinakamalaki at pinakamaliit na halaga ng function.

Sa isang bukas na pagitan

Sa ika-apat na figure, ang function ay tumatagal ng pinakamalaking (max y) at pinakamaliit (min y) na mga halaga sa mga nakatigil na punto na matatagpuan sa loob ng bukas na pagitan (-6;6).

Sa agwat , walang mga konklusyon ang maaaring makuha tungkol sa pinakamalaking halaga.

Sa infinity

Sa halimbawang ipinakita sa ikapitong figure, ang function ay tumatagal ng pinakamalaking halaga (max y) sa isang nakatigil na punto na may abscissa x=1, at ang pinakamaliit na halaga (min y) ay nakakamit sa kanang hangganan ng pagitan. Sa minus infinity, ang mga halaga ng function ay asymptotically lumalapit sa y=3.

Sa paglipas ng pagitan, ang function ay hindi umabot sa pinakamaliit o pinakamalaking halaga. Habang lumalapit ang x=2 mula sa kanan, ang mga value ng function ay may posibilidad na minus infinity (ang linyang x=2 ay isang vertical asymptote), at habang ang abscissa ay may posibilidad na plus infinity, ang mga value ng function ay asymptotically lumalapit sa y=3. Ang isang graphic na paglalarawan ng halimbawang ito ay ipinapakita sa Figure 8.

Algorithm para sa paghahanap ng pinakamalaki at pinakamaliit na halaga ng tuluy-tuloy na function sa isang segment.

Sumulat tayo ng isang algorithm na nagbibigay-daan sa amin upang mahanap ang pinakamalaki at pinakamaliit na halaga ng isang function sa isang segment.

1. Hinahanap namin ang domain ng kahulugan ng function at suriin kung naglalaman ito ng buong segment.
2. Nahanap namin ang lahat ng mga punto kung saan ang unang derivative ay hindi umiiral at kung saan ay nakapaloob sa segment (kadalasan ang mga naturang punto ay matatagpuan sa mga function na may argumento sa ilalim ng modulus sign at sa mga power function na may fractional-rational exponent). Kung walang ganoong mga punto, pagkatapos ay magpatuloy sa susunod na punto.
3. Tinutukoy namin ang lahat ng mga nakatigil na punto na nasa loob ng segment. Upang gawin ito, itinutumbas namin ito sa zero, lutasin ang nagresultang equation at pumili ng angkop na mga ugat. Kung walang mga nakatigil na punto o wala sa mga ito ang nahuhulog sa segment, pagkatapos ay magpatuloy sa susunod na punto.
4. Kinakalkula namin ang mga halaga ng function sa mga napiling nakatigil na mga punto (kung mayroon man), sa mga punto kung saan ang unang derivative ay hindi umiiral (kung mayroon man), pati na rin sa x=a at x=b.
5. Mula sa nakuha na mga halaga ng pag-andar, pipiliin namin ang pinakamalaki at pinakamaliit - sila ang kinakailangang pinakamalaki at pinakamaliit na halaga ng pag-andar, ayon sa pagkakabanggit.

Suriin natin ang algorithm para sa paglutas ng isang halimbawa upang mahanap ang pinakamalaki at pinakamaliit na halaga ng isang function sa isang segment.

Halimbawa.

Hanapin ang pinakamalaki at pinakamaliit na halaga ng isang function

• sa segment;
• sa segment [-4;-1] .

Solusyon.

Ang domain ng kahulugan ng isang function ay ang buong hanay ng mga tunay na numero, maliban sa zero, iyon ay. Ang parehong mga segment ay nasa loob ng domain ng kahulugan.

Hanapin ang derivative ng function na may kinalaman sa:

Malinaw, ang derivative ng function ay umiiral sa lahat ng mga punto ng mga segment at [-4;-1].

Tinutukoy namin ang mga nakatigil na puntos mula sa equation. Ang tanging tunay na ugat ay x=2. Ang nakatigil na puntong ito ay nahuhulog sa unang bahagi.

Para sa unang kaso, kinakalkula namin ang mga halaga ng function sa mga dulo ng segment at sa nakatigil na punto, iyon ay, para sa x=1, x=2 at x=4:

Samakatuwid, ang pinakamalaking halaga ng function ay nakamit sa x=1, at ang pinakamaliit na halaga – sa x=2.

Para sa pangalawang kaso, kinakalkula namin ang mga halaga ng function lamang sa mga dulo ng segment [-4;-1] (dahil hindi ito naglalaman ng isang nakatigil na punto):

Solusyon.

Magsimula tayo sa domain ng function. Ang square trinomial sa denominator ng fraction ay hindi dapat maglaho:

Madaling suriin na ang lahat ng mga pagitan mula sa pahayag ng problema ay nabibilang sa domain ng kahulugan ng function.

Ibahin natin ang function:

Malinaw, ang derivative ay umiiral sa buong domain ng kahulugan ng function.

Maghanap tayo ng mga nakatigil na puntos. Ang derivative ay napupunta sa zero sa . Ang nakatigil na puntong ito ay nasa loob ng mga pagitan (-3;1] at (-3;2).

Ngayon ay maaari mong ihambing ang mga resulta na nakuha sa bawat punto sa graph ng function. Ang mga asul na tuldok na linya ay nagpapahiwatig ng mga asymptotes.

Sa puntong ito maaari nating tapusin ang paghahanap ng pinakamalaki at pinakamaliit na halaga ng function. Ang mga algorithm na tinalakay sa artikulong ito ay nagbibigay-daan sa iyo na makakuha ng mga resulta na may pinakamababang pagkilos. Gayunpaman, maaari itong maging kapaki-pakinabang upang matukoy muna ang mga pagitan ng pagtaas at pagbaba ng function at pagkatapos lamang na gumawa ng mga konklusyon tungkol sa pinakamalaki at pinakamaliit na halaga ng function sa anumang agwat. Nagbibigay ito ng mas malinaw na larawan at mahigpit na katwiran para sa mga resulta.

Kahulugan3 . 3 Hayaan ang ilang function, ang domain ng kahulugan nito, at ilang (bukas) na pagitan (maaaring may at/o ) 7 . Tawagan natin ang function tuloy-tuloy sa pagitan, kung tuluy-tuloy sa anumang punto, iyon ay, para sa anumang mayroon (sa pinaikling anyo:

Hayaan ngayon na maging isang (sarado) na segment sa . Tawagan natin ang function tuloy-tuloy sa segment, kung tuloy-tuloy sa pagitan, tuloy-tuloy sa kanan sa punto at tuloy-tuloy sa kaliwa sa punto, ibig sabihin

Halimbawa3 . 13 Isaalang-alang ang function (Heaviside function) sa segment , . Pagkatapos ito ay tuloy-tuloy sa segment (sa kabila ng katotohanan na sa puntong ito ay may discontinuity ng unang uri).

Fig. 3.15 Graph ng function ng Heaviside

Ang isang katulad na kahulugan ay maaaring ibigay para sa kalahating pagitan ng form at , kabilang ang mga kaso at . Gayunpaman, maaari nating gawing pangkalahatan ang kahulugang ito sa kaso ng isang arbitrary na subset tulad ng sumusunod. Ipakilala muna natin ang konsepto sapilitan sa mga base: hayaang maging isang base na ang lahat ng mga dulo ay may walang laman na intersection na may . Ipahiwatig natin sa pamamagitan ng at isaalang-alang ang set ng lahat. Ito ay pagkatapos ay madaling suriin na ang set magiging basehan. Kaya, para sa mga base , at , kung saan , at ang mga base ng hindi nabutas na dalawang panig (kaliwa, kanan, ayon sa pagkakabanggit) na mga kapitbahayan ng isang punto (tingnan ang kanilang kahulugan sa simula ng kasalukuyang kabanata).

Kahulugan3 . 4 Tawagan natin ang function tuloy-tuloy sa set, Kung

Madaling makita na sa at sa kahulugang ito ay tumutugma sa mga ibinigay sa itaas partikular para sa pagitan at segment.

Alalahanin na ang lahat ng elementarya ay tuluy-tuloy sa lahat ng mga punto ng kanilang mga domain ng kahulugan at, samakatuwid, tuluy-tuloy sa anumang mga pagitan at mga segment na nasa kanilang mga domain ng kahulugan.

Dahil ang continuity sa isang interval at segment ay tinukoy sa pointwise, ang theorem hold, na isang agarang resulta ng Theorem 3.1:

Teorama3 . 5 Hayaan At -- mga function at -- pagitan o segment na nakalagay . Hayaan At tuloy-tuloy para sa . Pagkatapos ang mga pag-andar , , tuloy-tuloy para sa . Kung sa karagdagan sa harap ng lahat , pagkatapos ay ang function ay tuloy-tuloy din sa .

Ang sumusunod na pahayag ay sumusunod mula sa theorem na ito, tulad ng mula sa Theorem 3.1 - Proposisyon 3.3:

Alok3 . 4 Isang grupo ng lahat ng function ay tuloy-tuloy sa isang interval o segment -- ito ay isang linear na espasyo:

Ang isang mas kumplikadong pag-aari ng isang tuluy-tuloy na pag-andar ay ipinahayag ng sumusunod na teorama.

Teorama3 . 6 (tungkol sa ugat ng tuluy-tuloy na pag-andar) Hayaan ang function tuloy-tuloy sa segment , at At -- bilang ng iba't ibang palatandaan. (Para sa katiyakan, ipagpalagay natin iyon , A .) Pagkatapos ay mayroong kahit isang ganoong halaga , Ano (iyon ay, mayroong kahit isang ugat mga equation ).

Patunay. Tingnan natin ang gitna ng segment. Pagkatapos ito ay alinman, o, o. Sa unang kaso, ang ugat ay matatagpuan: ito ay . Sa natitirang dalawang kaso, isaalang-alang ang bahaging iyon ng segment sa mga dulo kung saan ang function ay kumukuha ng mga halaga ng iba't ibang mga palatandaan: sa kaso o sa kaso . Tinutukoy namin ang napiling kalahati ng segment sa pamamagitan ng at inilapat ang parehong pamamaraan dito: hatiin ito sa dalawang kalahati at , kung saan , at hanapin . Kung sakaling matagpuan ang ugat; kung sakaling isaalang-alang pa natin ang segment , kung sakaling - segment atbp.

Fig. 3.16. Magkakasunod na dibisyon ng isang segment sa kalahati

Nakuha namin na alinman sa ilang hakbang ay mahahanap ang ugat, o isang sistema ng mga nested na segment ay bubuo

kung saan ang bawat kasunod na segment ay kalahati ng haba ng nauna. Ang pagkakasunod-sunod ay hindi bumababa at may hangganan mula sa itaas (halimbawa, sa pamamagitan ng numero); samakatuwid (sa pamamagitan ng Theorem 2.13), ito ay may limitasyon. Kasunod - hindi tumataas at may hangganan sa ibaba (halimbawa, ayon sa numero ); ibig sabihin may limitasyon. Dahil ang mga haba ng mga segment ay bumubuo ng isang bumababang geometric na pag-unlad (na may denominator ), sila ay may posibilidad na 0, at , yan ay . Ilagay natin ngayon. Pagkatapos

At

dahil tuluy-tuloy ang function. Gayunpaman, sa pamamagitan ng pagbuo ng mga pagkakasunud-sunod at , at , upang, sa pamamagitan ng theorem sa pagpasa sa limitasyon sa hindi pagkakapantay-pantay (Theorem 2.7), at , iyon ay, at . Nangangahulugan ito na , at ang ugat ng equation.

Halimbawa3 . 14 Isaalang-alang ang function sa segment. Dahil at mga numero ng iba't ibang mga palatandaan, ang function ay nagiging 0 sa ilang mga punto sa pagitan. Nangangahulugan ito na ang equation ay may ugat.

Fig. 3.17 Graphical na representasyon ng ugat ng equation

Ang napatunayang theorem ay talagang nagbibigay sa atin ng isang paraan upang mahanap ang ugat, kahit man lang tinatayang, na may anumang antas ng katumpakan na tinukoy nang maaga. Ito ang paraan ng paghahati ng isang segment sa kalahati, na inilarawan sa patunay ng theorem. Makikilala natin ito at ang iba pang mas epektibong pamamaraan ng humigit-kumulang na paghahanap ng ugat nang mas detalyado sa ibaba, pagkatapos nating pag-aralan ang konsepto at katangian ng isang derivative.

Tandaan na ang teorama ay hindi nagsasaad na kung ang mga kondisyon nito ay natutugunan, kung gayon ang ugat ay natatangi. Tulad ng ipinapakita ng sumusunod na figure, maaaring mayroong higit sa isang ugat (mayroong 3 sa figure).

Fig. 3.18. Maraming mga ugat ng isang function na kumukuha ng mga halaga ng iba't ibang mga palatandaan sa mga dulo ng segment

Gayunpaman, kung ang isang function ay monotonically tumaas o monotonically bumababa sa isang segment, sa mga dulo kung saan ito ay tumatagal ng mga halaga ng iba't ibang mga palatandaan, kung gayon ang ugat ay natatangi, dahil ang isang mahigpit na monotone function ay tumatagal ng bawat isa sa mga halaga nito sa eksaktong isang punto , kasama ang halagang 0.

Fig. 3.19 Ang isang monotonic function ay hindi maaaring magkaroon ng higit sa isang ugat

Ang isang agarang kahihinatnan ng theorem sa ugat ng isang tuluy-tuloy na function ay ang sumusunod na theorem, na sa kanyang sarili ay napakahalaga sa mathematical analysis.

Teorama3 . 7 (tungkol sa intermediate na halaga ng isang tuluy-tuloy na function) Hayaan ang function tuloy-tuloy sa segment At (para sa katiyakan ay ipagpalagay natin na ). Hayaan -- ilang numero na nasa pagitan At . Pagkatapos ay mayroong ganoong punto , Ano .

Fig. 3.20. Ang patuloy na pag-andar ay tumatagal ng anumang intermediate na halaga

Patunay. Isaalang-alang ang function ng helper , Saan . Pagkatapos At . Ang function ay malinaw na tuloy-tuloy, at sa pamamagitan ng nakaraang teorama mayroong isang punto tulad na . Ngunit ang pagkakapantay-pantay na ito ay nangangahulugan na .

Tandaan na kung ang function ay hindi tuloy-tuloy, maaaring hindi ito tumagal ng lahat ng mga intermediate na halaga. Halimbawa, ang function ng Heaviside (tingnan ang Halimbawa 3.13) ay kumukuha ng mga halaga, , ngunit wala kahit saan, kasama ang pagitan, ay tumatagal, halimbawa, isang intermediate na halaga. Ang katotohanan ay ang function ng Heaviside ay may discontinuity sa isang puntong eksaktong nasa pagitan.

Upang higit pang pag-aralan ang mga katangian ng mga function na tuluy-tuloy sa isang agwat, kakailanganin natin ang sumusunod na banayad na pag-aari ng sistema ng mga tunay na numero (nabanggit na natin ito sa Kabanata 2 na may kaugnayan sa teorama sa limitasyon ng isang monotonically na pagtaas ng bounded function): para sa anumang set na may hangganan sa ibaba (iyon ay, para sa lahat at ilan; ang numero ay tinatawag babang dulo set) na magagamit eksaktong ilalim na gilid, iyon ay, ang pinakamalaki sa mga bilang na para sa lahat . Katulad nito, kung ang isang set ay nakatali sa itaas, kung gayon mayroon ito eksaktong upper bound: ito ang pinakamaliit sa mga nangungunang mukha(para sa lahat).

Fig. 3.21 Lower at upper bounds ng isang bounded set

Kung , kung gayon mayroong hindi tumataas na pagkakasunud-sunod ng mga puntos na may posibilidad na . Sa parehong paraan, kung , pagkatapos ay mayroong isang hindi bumababa na pagkakasunud-sunod ng mga puntos na may posibilidad na .

Kung ang isang punto ay kabilang sa set, kung gayon ito ang pinakamaliit na elemento ng set na ito: ; katulad kung , Yung .

Bilang karagdagan, para sa karagdagang kakailanganin natin ang sumusunod

Lemma3 . 1 Hayaan -- tuloy-tuloy na paggana sa isang segment , at marami ang mga puntong iyon , kung saan (o , o ) ay walang laman. Pagkatapos sa kasaganaan may pinakamaliit na halaga , ganyan sa harap ng lahat .

Fig. 3.22. Ang pinakamaliit na argumento kung saan kinukuha ng function ang tinukoy na halaga

Patunay. Dahil ito ay isang bounded set (ito ay bahagi ng isang segment), mayroon itong infimum. Pagkatapos ay mayroong isang hindi tumataas na pagkakasunud-sunod , , tulad na para sa . Bukod dito, sa pamamagitan ng kahulugan ng isang set. Samakatuwid, ang pagpasa sa limitasyon, nakukuha natin, sa isang banda,

at sa kabilang banda, dahil sa pagpapatuloy ng pag-andar,

Ang ibig sabihin nito ay , kaya ang punto ay kabilang sa set at .

Sa kaso kapag ang set ay tinukoy ng hindi pagkakapantay-pantay, mayroon tayo para sa lahat at sa pamamagitan ng theorem sa pagpasa sa limitasyon sa hindi pagkakapantay-pantay na nakuha natin

mula saan , na ang ibig sabihin ay at . Katulad nito, sa kaso ng hindi pagkakapantay-pantay, ang pagpasa sa limitasyon sa hindi pagkakapantay-pantay ay nagbibigay

mula saan, at.

Teorama3 . 8 (tungkol sa hangganan ng isang tuluy-tuloy na pag-andar) Hayaan ang function tuloy-tuloy sa segment . Pagkatapos limitado sa , ibig sabihin, mayroong ganoong pare-pareho , Ano sa harap ng lahat .

Fig. 3.23 Ang isang function na tuloy-tuloy sa isang segment ay may hangganan

Patunay. Ipagpalagay natin ang kabaligtaran: huwag itong limitahan, halimbawa, mula sa itaas. Kung gayon ang lahat ng set , , , ay hindi walang laman. Sa pamamagitan ng nakaraang lemma, ang bawat isa sa mga set na ito ay may pinakamaliit na halaga , . Ipakita natin yan

Talaga, . Kung ang anumang punto mula sa , halimbawa, ay nasa pagitan ng at , pagkatapos

iyon ay, isang intermediate na halaga sa pagitan ng at . Nangangahulugan ito, sa pamamagitan ng teorama sa intermediate na halaga ng isang tuluy-tuloy na pag-andar, mayroong isang puntong ganoon , At . Ngunit, salungat sa palagay na - ang pinakamaliit na halaga ng set. Ito ay sumusunod na para sa lahat.

Sa parehong paraan, higit na napatunayan na para sa lahat , para sa lahat , atbp. Kaya, ay isang pagtaas ng pagkakasunod-sunod na nililimitahan ng numero sa itaas. Samakatuwid ito ay umiiral. Mula sa pagpapatuloy ng pag-andar ay sumusunod na mayroong , Ngunit sa , kaya walang limitasyon. Ang resultang kontradiksyon ay nagpapatunay na ang function ay nakatali sa itaas.

Ito ay pinatunayan sa isang katulad na paraan na ito ay nakatali mula sa ibaba, na nagpapahiwatig ng pahayag ng teorama.

Malinaw, imposibleng pahinain ang mga kondisyon ng theorem: kung ang isang function ay hindi tuloy-tuloy, kung gayon hindi ito kailangang itali sa isang pagitan (ibinibigay namin bilang isang halimbawa ang function

sa segment. Ang function na ito ay hindi nakatali sa pagitan, dahil ang at ay may discontinuity point ng pangalawang uri, tulad na sa . Imposible ring palitan ang isang segment sa kondisyon ng theorem na may pagitan o kalahating pagitan: bilang isang halimbawa, isaalang-alang ang parehong function sa isang kalahating pagitan. Ang function ay tuloy-tuloy sa kalahating pagitan na ito, ngunit walang hangganan, dahil sa katotohanan na sa .

Ang paghahanap ng pinakamahusay na mga constant na maaaring magamit upang limitahan ang isang function mula sa itaas at ibaba sa isang naibigay na pagitan ay natural na humahantong sa amin sa problema ng paghahanap ng minimum at maximum ng isang tuluy-tuloy na function sa pagitan na ito. Ang posibilidad ng paglutas ng problemang ito ay inilarawan ng sumusunod na teorama.

Teorama3 . 9 (tungkol sa pag-abot sa isang extremum sa pamamagitan ng tuluy-tuloy na pag-andar) Hayaan ang function tuloy-tuloy sa segment . Tapos may punto , ganyan sa harap ng lahat (yan ay -- pinakamababang punto: ), at may punto , ganyan sa harap ng lahat (yan ay -- pinakamataas na punto: ). Sa madaling salita, ang minimum at maximum 8 Ang mga halaga ng isang tuluy-tuloy na function sa isang segment ay umiiral at nakakamit sa ilang mga punto At ang segment na ito.

Fig. 3.24 Ang isang function na tuloy-tuloy sa isang segment ay umabot sa maximum at minimum

Patunay. Dahil, ayon sa nakaraang teorama, ang function ay nakatali sa itaas, pagkatapos ay mayroong isang eksaktong upper bound para sa mga halaga ng function sa pamamagitan ng -- numero . Kaya, ang mga set , ,..., ,..., ay hindi walang laman, at sa nakaraang lemma naglalaman sila ng pinakamaliit na halaga : , . Ang mga ito ay hindi bumababa (ang pahayag na ito ay napatunayan sa eksaktong parehong paraan tulad ng sa nakaraang teorama):

at nililimitahan mula sa itaas ng . Samakatuwid, ayon sa theorem sa limitasyon ng isang monotone bounded sequence, mayroong limitasyon Since , pagkatapos

sa pamamagitan ng theorem sa pagpasa sa limitasyon sa hindi pagkakapantay-pantay, iyon ay, . Ngunit sa lahat, kasama na. Mula dito lumalabas na , iyon ay, ang maximum ng function ay nakakamit sa punto .

Ang pagkakaroon ng pinakamababang punto ay napatunayan sa katulad na paraan.

Sa teorama na ito, tulad ng sa naunang isa, imposibleng pahinain ang mga kondisyon: kung ang pag-andar ay hindi tuloy-tuloy, kung gayon maaaring hindi nito maabot ang maximum o minimum na halaga nito sa segment, kahit na ito ay limitado. Halimbawa, kunin natin ang function

sa segment. Ang function na ito ay nakatali sa pagitan (malinaw naman) at , gayunpaman, hindi nito kinukuha ang halaga 1 sa anumang punto ng segment (tandaan na , hindi 1). Ang katotohanan ay ang function na ito ay may discontinuity ng unang uri sa point , kaya na sa limitasyon ay hindi katumbas ng halaga ng function sa point 0. Dagdag pa, isang tuluy-tuloy na function na tinukoy sa isang interval o iba pang set na hindi ang isang saradong segment (sa isang kalahating pagitan, kalahating axis) ay maaari ding hindi kumuha ng matinding halaga. Bilang halimbawa, isaalang-alang ang isang function sa pagitan . Malinaw na ang function ay tuloy-tuloy at iyon at , gayunpaman, ang function ay hindi kumukuha ng value 0 o value 1 sa anumang punto sa pagitan . Isaalang-alang din natin ang pag-andar sa axle shaft. Ang function na ito ay tuloy-tuloy sa , tumataas, kumukuha ng pinakamababang halaga nito na 0 sa punto , ngunit hindi kumukuha ng maximum na halaga sa anumang punto (bagaman ito ay limitado mula sa itaas ng numero at

Kahulugan. Kung ang function f(x) ay tinukoy sa pagitan [ a, b], ay tuloy-tuloy sa bawat punto ng pagitan ( a, b), sa punto a tuloy-tuloy sa kanan, sa punto b ay tuloy-tuloy sa kaliwa, pagkatapos ay sinasabi namin na ang function f(x) tuloy-tuloy sa segment [a, b].

Sa madaling salita, ang function f(x) ay tuloy-tuloy sa pagitan [ a, b], kung ang tatlong kundisyon ay natutugunan:

1) "x 0 Î( a, b): f(x) = f(x 0);

2) f(x) = f(a);

3) f(x) = f(b).

Para sa mga function na tuluy-tuloy sa isang agwat, isinasaalang-alang namin ang ilang mga katangian, na aming binabalangkas sa anyo ng mga sumusunod na theorems, nang hindi nagsasagawa ng mga patunay.

Teorama 1. Kung ang function f(x) ay tuloy-tuloy sa pagitan [ a, b], pagkatapos ay maabot nito ang pinakamababa at pinakamataas na halaga nito sa segment na ito.

Ang teorama na ito ay nagsasaad (Larawan 1.15) na sa segment [ a, b] may ganyang punto x 1 iyon f(x 1) £ f(x) para sa alinman x mula sa [ a, b] at mayroong isang punto x 2 (x 2 О[ a, b]) ganyan" xÎ[ a, b] (f(x 2)³ f(x)).

Ibig sabihin f(x 1) ay ang pinakamalaking para sa isang naibigay na function sa [ a, b], A f(x 2) - ang pinakamaliit. Tukuyin natin: f(x 1) = M, f(x 2) =m. Dahil para sa f(x) ang hindi pagkakapantay-pantay ay mayroong: " xÎ[ a, b] m£ f(x) £ M, pagkatapos ay makuha natin ang sumusunod na corollary mula sa Theorem 1.

Bunga. Kung ang function f(x) ay tuloy-tuloy sa isang pagitan, pagkatapos ito ay nakatali sa pagitan na ito.

Teorama 2. Kung ang function f(x) ay tuloy-tuloy sa pagitan [ a,b] at sa mga dulo ng segment ay kumukuha ng mga halaga ng iba't ibang mga palatandaan, pagkatapos ay mayroong isang panloob na punto x 0 segment [ a, b], kung saan ang function ay nagiging 0, i.e. $ x 0 Î ( a, b) (f(x 0) = 0).

Ang theorem na ito ay nagsasaad na ang graph ng isang function y = f(x), tuloy-tuloy sa pagitan [ a, b], bumabagtas sa axis baka kahit isang beses kung ang mga halaga f(a) At f(b) may magkasalungat na mga palatandaan. Kaya, (Larawan 1.16) f(a) > 0, f(b) < 0 и функция f(x) nagiging 0 sa mga puntos x 1 , x 2 , x 3 .

Teorama 3. Hayaan ang function f(x) ay tuloy-tuloy sa pagitan [ a, b], f(a) = A, f(b) = B At A¹ B. (Larawan 1.17). Pagkatapos ay para sa anumang numero C, nakapaloob sa pagitan ng mga numero A At B, may ganoong interior point x 0 segment [ a, b], Ano f(x 0) = C.

Bunga. Kung ang function f(x) ay tuloy-tuloy sa pagitan [ a, b], m– pinakamaliit na halaga f(x), M– ang pinakamalaking halaga ng function f(x) sa segment [ a, b], pagkatapos ang function ay tumatagal (kahit isang beses) ng anumang halaga m, nagtapos sa pagitan ng m At M, at samakatuwid ang segment [ m, M] ay ang set ng lahat ng value ng function f(x) sa segment [ a, b].

Tandaan na kung ang isang function ay tuloy-tuloy sa pagitan ( a, b) o mayroon sa segment [ a, b] discontinuity points, pagkatapos ay Theorems 1, 2, 3 para sa naturang function ay hindi na totoo.

Sa konklusyon, isaalang-alang ang theorem sa pagkakaroon ng isang inverse function.

Teorama 4. Hayaan f(x) ay tuloy-tuloy sa pagitan X, tumataas (o bumababa) ng X at may hanay ng mga halaga Y. Pagkatapos ay para sa pag-andar y = f(x) mayroong isang kabaligtaran na pag-andar x= j(y), tinukoy sa pagitan Y, tuloy-tuloy at tumataas (o bumababa) ng Y na may maraming kahulugan X.

Magkomento. Hayaan ang function x= j(y) ay ang kabaligtaran ng function f(x). Dahil ang argumento ay karaniwang tinutukoy ng x, at ang function sa pamamagitan ng y, pagkatapos ay isusulat namin ang inverse function sa form y =j(x).

Halimbawa 1. Function y = x 2 (Larawan 1.8, a) sa set X= }