ფუნქციების თვისებები, რომლებიც უწყვეტია ინტერვიუზე

განვიხილოთ ფუნქციების ზოგიერთი თვისება უწყვეტი ინტერვალზე. ჩვენ წარმოგიდგენთ ამ თვისებებს მტკიცებულების გარეშე.

ფუნქცია y = f(x)დაურეკა უწყვეტი სეგმენტზე [ა, ბ], თუ იგი უწყვეტია ამ სეგმენტის ყველა შიდა წერტილში და მის ბოლოებზე, ე.ი. წერტილებში ადა ბ, უწყვეტია მარჯვნივ და მარცხნივ, შესაბამისად.

თეორემა 1.უწყვეტი ფუნქცია ინტერვალზე [ ა, ბ], ამ სეგმენტის ერთ წერტილში მაინც იღებს ყველაზე დიდ მნიშვნელობას და ერთ წერტილში მაინც უმცირესს.

თეორემა ამბობს, რომ თუ ფუნქცია y = f(x)არის უწყვეტი ინტერვალზე [ ა, ბ], მაშინ არის მინიმუმ ერთი წერტილი x 1 Î [ ა, ბ] ისეთი, რომ ფუნქციის მნიშვნელობა f(x)ამ ეტაპზე ყველაზე დიდი იქნება ამ სეგმენტზე მისი მნიშვნელობებიდან: f(x 1) ≥ f(x). ანალოგიურად, არსებობს ასეთი წერტილი x 2, რომელშიც ფუნქციის მნიშვნელობა იქნება სეგმენტის ყველა მნიშვნელობიდან ყველაზე პატარა: f(x 1) ≤ f(x).

ნათელია, რომ შეიძლება იყოს რამდენიმე ასეთი წერტილი, მაგალითად, ფიგურა აჩვენებს, რომ ფუნქცია f(x)იღებს უმცირეს მნიშვნელობას ორ წერტილში x 2და x 2 ".

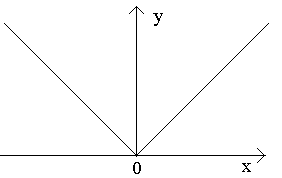
კომენტარი. თეორემის განცხადება შეიძლება არასწორი გახდეს, თუ გავითვალისწინებთ ფუნქციის მნიშვნელობას ინტერვალზე ( ა, ბ). მართლაც, თუ გავითვალისწინებთ ფუნქციას y = x(0, 2), შემდეგ ის უწყვეტია ამ ინტერვალზე, მაგრამ არ აღწევს მასში არც უდიდეს და არც უმცირეს მნიშვნელობებს: ის აღწევს ამ მნიშვნელობებს ინტერვალის ბოლოებში, მაგრამ ბოლოები არ ეკუთვნის. ჩვენს დომენზე.

ასევე, თეორემა წყვეტს ჭეშმარიტებას უწყვეტი ფუნქციებისთვის. მიეცი მაგალითი.

შედეგი.თუ ფუნქცია f(x)უწყვეტია [ ა, ბ], მაშინ ის შეზღუდულია ამ სეგმენტზე.

თეორემა 2.დაუშვით ფუნქცია y = f(x)არის უწყვეტი ინტერვალზე [ ა, ბ] და ამ სეგმენტის ბოლოებში იღებს სხვადასხვა ნიშნის მნიშვნელობებს, მაშინ სეგმენტის შიგნით არის მინიმუმ ერთი წერტილი x = C, რომელშიც ფუნქცია მიდის ნულზე: f(C)= 0, სადაც a< C< b

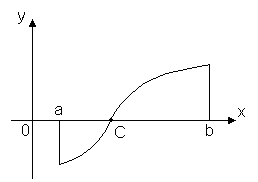
ამ თეორემას აქვს მარტივი გეომეტრიული მნიშვნელობა: თუ უწყვეტი ფუნქციის გრაფიკის წერტილები y = f(x)სეგმენტის ბოლოების შესაბამისი [ ა, ბ] დაწექი ღერძის მოპირდაპირე მხარეს ოქსი, მაშინ ეს გრაფიკი კვეთს ღერძს სეგმენტის მინიმუმ ერთ წერტილში ოქსი. უწყვეტ ფუნქციებს შეიძლება არ ჰქონდეს ეს თვისება.

ეს თეორემა აღიარებს შემდეგ განზოგადებას.

თეორემა 3 (შუალედური ღირებულების თეორემა).დაუშვით ფუნქცია y = f(x)არის უწყვეტი ინტერვალზე [ ა, ბ] და f(a) = A, f(b) = B. შემდეგ ნებისმიერი ნომრისთვის Cშორის დადებული ადა ბამ სეგმენტის შიგნით არის ასეთი წერტილი CÎ [ ა, ბ], Რა f(c) = C.

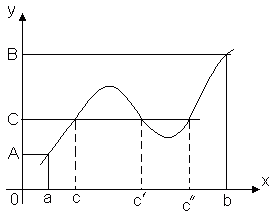
ეს თეორემა გეომეტრიულად აშკარაა. განვიხილოთ ფუნქციის გრაფიკი y = f(x). დაე f(a) = A, f(b) = B. შემდეგ ნებისმიერი სწორი ხაზი y = C, სად C- ნებისმიერი რიცხვი შორის ადა ბ, ერთ წერტილში მაინც გადაკვეთს ფუნქციის გრაფიკს. გადაკვეთის წერტილის აბსცისა იქნება ეს მნიშვნელობა x = C, რომელიც f(c) = C.

ამრიგად, უწყვეტი ფუნქცია, რომელიც გადადის ერთი მნიშვნელობიდან მეორეზე, აუცილებლად გადის ყველა შუალედურ მნიშვნელობას. Კერძოდ:

შედეგი.თუ ფუნქცია y = f(x)არის უწყვეტი გარკვეული ინტერვალით და იღებს უდიდეს და უმცირეს მნიშვნელობებს, შემდეგ ამ ინტერვალზე ერთხელ მაინც იღებს ნებისმიერ მნიშვნელობას, რომელიც შეიცავს მის უმცირეს და უდიდეს მნიშვნელობებს შორის.

წარმოებული და მისი აპლიკაციები. წარმოებულის განმარტება

მოდით, გარკვეული ფუნქცია გვქონდეს y=f(x),განსაზღვრულია გარკვეული ინტერვალით. თითოეული არგუმენტის მნიშვნელობისთვის xამ ინტერვალიდან ფუნქცია y=f(x)აქვს გარკვეული მნიშვნელობა.

განვიხილოთ ორი არგუმენტის მნიშვნელობა: საწყისი x 0 და ახალი x.

განსხვავება x–x 0 ეწოდება x არგუმენტის გაზრდითწერტილში x 0 და აღინიშნება Δx. ამრიგად, Δx = x – x 0 (არგუმენტის ზრდა შეიძლება იყოს დადებითი ან უარყოფითი). ამ თანასწორობიდან გამომდინარეობს, რომ x=x 0 +Δx, ე.ი. ცვლადის საწყისმა მნიშვნელობამ მიიღო გარკვეული ზრდა. მაშინ, თუ წერტილში x 0 ფუნქციის მნიშვნელობა იყო f(x 0 ), შემდეგ ახალ წერტილში xფუნქცია მიიღებს მნიშვნელობას f(x) = f(x 0 +Δx).

განსხვავება წ–წ 0 = f(x) – f(x 0 ) დაურეკა ფუნქციის ზრდა y = f(x)წერტილში x 0 და მითითებულია სიმბოლოთი Δy. ამრიგად,

როგორც წესი, არგუმენტის საწყისი მნიშვნელობა x 0 ითვლება ფიქსირებულად, ხოლო ახალი მნიშვნელობა x- ცვლადი. მერე წ 0 = f(x 0 ) მუდმივი აღმოჩნდება და y = f(x)- ცვლადი. მატება Δyდა Δxასევე იქნება ცვლადები და ფორმულა (1) აჩვენებს, რომ Dyარის ცვლადის ფუნქცია Δx.

შევქმნათ ფუნქციის ზრდის შეფარდება არგუმენტის ზრდასთან

მოდით ვიპოვოთ ამ თანაფარდობის ზღვარი ზე Δx→0. თუ ეს ზღვარი არსებობს, მაშინ მას ამ ფუნქციის წარმოებული ეწოდება f(x)წერტილში x 0 და აღვნიშნავთ ვ "(x 0). Ისე,

წარმოებულიამ ფუნქციას y = f(x)წერტილში x 0 ეწოდება Δ ფუნქციის ზრდის კოეფიციენტის ზღვარს წარგუმენტის ზრდა Δ x, როდესაც ეს უკანასკნელი თვითნებურად იხრება ნულისკენ.

გაითვალისწინეთ, რომ ერთი და იგივე ფუნქციისთვის წარმოებული სხვადასხვა წერტილში xშეუძლია მიიღოს სხვადასხვა ღირებულებები, ე.ი. წარმოებული შეიძლება ჩაითვალოს არგუმენტის ფუნქციად x. ეს ფუნქცია დანიშნულია ვ "(x)

წარმოებული აღინიშნება სიმბოლოებით ვ "(x), y", . წარმოებულის სპეციფიკური მნიშვნელობა ზე x = aაღინიშნება ვ "(ა) ან წ "| x=a.

ფუნქციის წარმოებულის პოვნის ოპერაცია f(x)ეწოდება ამ ფუნქციის დიფერენციაცია.

წარმოებულის განმარტებით პირდაპირ მოსაძებნად, შეგიძლიათ გამოიყენოთ შემდეგი: ემპირიული წესი:

მაგალითები.

წარმოებულის მექანიკური გრძნობა

ფიზიკიდან ცნობილია, რომ ერთგვაროვანი მოძრაობის კანონს აქვს ფორმა s = v t, სად ს– გზამ გაიარა დროის მომენტამდე ტ, ვ- ერთიანი მოძრაობის სიჩქარე.

თუმცა იმის გამო ბუნებაში მოძრაობების უმეტესობა არათანაბარია, შემდეგ ზოგადად სიჩქარე და, შესაბამისად, მანძილი სდროზე იქნება დამოკიდებული ტ, ე.ი. დროის ფუნქცია იქნება.

ასე რომ, მატერიალური წერტილი კანონის მიხედვით ერთი მიმართულებით მოძრაობდეს სწორი ხაზით s=s(t).

მოდით აღვნიშნოთ დროის გარკვეული მომენტი ტ 0 . ამ დროს პუნქტმა გზა გაიარა s=s(t 0 ). მოდით განვსაზღვროთ სიჩქარე ვმატერიალური წერტილი დროის მომენტში ტ 0 .

ამისათვის მოდით განვიხილოთ დროის სხვა მომენტი ტ 0 + Δ ტ. იგი შეესაბამება გავლილ გზას s =s(t 0 + Δ ტ). შემდეგ გარკვეული პერიოდის განმავლობაში Δ ტწერტილმა გაიარა Δs გზა =s(t 0 + Δ უ)–s(t).

განვიხილოთ დამოკიდებულება. მას ეწოდება საშუალო სიჩქარე Δ დროის ინტერვალში ტ. საშუალო სიჩქარე არ შეუძლია ზუსტად დაახასიათოს სიჩქარე, რომლითაც მოძრაობს წერტილი მომენტში ტ 0 (რადგან მოძრაობა არათანაბარია). იმისათვის, რომ უფრო ზუსტად გამოვხატოთ ეს ჭეშმარიტი სიჩქარე საშუალო სიჩქარის გამოყენებით, საჭიროა უფრო მოკლე დროში Δ ტ.

ასე რომ, მოძრაობის სიჩქარე დროის მოცემულ მომენტში ტ 0 (მყისიერი სიჩქარე) არის საშუალო სიჩქარის ზღვარი დან ტ 0-მდე ტ 0 +Δ ტ, როდესაც Δ ტ→0:

,

იმათ. არათანაბარი სიჩქარეეს არის გავლილი მანძილის წარმოებული დროის მიმართ.

წარმოებულის გეომეტრიული მნიშვნელობა

ჯერ შემოვიღოთ მრუდის ტანგენტის განმარტება მოცემულ წერტილში.

მოდით გვქონდეს მრუდი და ფიქსირებული წერტილი მასზე M 0(იხილეთ სურათი). მეს მრუდი და დახაზეთ სეკანტი M 0 M. თუ წერტილი მიწყებს მოძრაობას მრუდის გასწვრივ და წერტილი M 0რჩება უმოძრაოდ, შემდეგ სეკანტი იცვლის თავის პოზიციას. თუ წერტილის შეუზღუდავი მიახლოებით მმრუდის გასწვრივ წერტილამდე M 0ნებისმიერ მხარეს სეკანტი მიდრეკილია დაიკავოს გარკვეული სწორი ხაზის პოზიცია M 0 T, შემდეგ პირდაპირ M 0 Tმოუწოდა მრუდის ტანგენტს მოცემულ წერტილში M 0.

რომ., ტანგენსიმრუდამდე მოცემულ წერტილში M 0სეკანტის ზღვრულ პოზიციას უწოდებენ M 0 Mროდესაც წერტილი მმიდრეკილია მრუდის გასწვრივ წერტილამდე M 0.

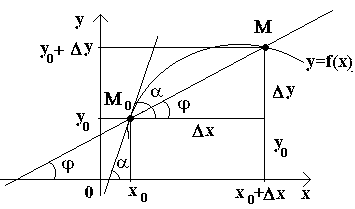
ახლა განვიხილოთ უწყვეტი ფუნქცია y=f(x)და ამ ფუნქციის შესაბამისი მრუდი. რაღაც ღირებულებით X 0 ფუნქცია იღებს მნიშვნელობას y 0 =f(x 0).ეს ღირებულებები x 0 და წმრუდეზე 0 შეესაბამება წერტილს M 0 (x 0 ; y 0).მოვიყვანოთ არგუმენტი x 0ნამატი Δ X. არგუმენტის ახალი მნიშვნელობა შეესაბამება ფუნქციის გაზრდილ მნიშვნელობას წ 0 +Δ y=f(x 0 –Δ x). ჩვენ ვიგებთ აზრს M(x 0+Δ x; y 0+Δ y).დავხატოთ სეკანტი M 0 Mდა ფ-ით აღვნიშნოთ ღერძის დადებითი მიმართულების სეკანტის მიერ წარმოქმნილი კუთხე ოქსი. შევქმნათ ურთიერთობა და შევამჩნიოთ, რომ .

თუ ახლა Δ x→0, მაშინ Δ ფუნქციის უწყვეტობის გამო ზე→0 და, შესაბამისად, წერტილი მ, რომელიც მოძრაობს მრუდის გასწვრივ, უახლოვდება წერტილს შეუზღუდავად M 0. შემდეგ სეკანტი M 0 Mმიდრეკილია დაიკავოს მრუდის ტანგენტის პოზიცია წერტილში M 0და კუთხე φ→α Δ-ზე x→0, სადაც α აღნიშნავს კუთხეს ღერძის ტანგენტსა და დადებით მიმართულებას შორის ოქსი. ვინაიდან tan φ ფუნქცია განუწყვეტლივ დამოკიდებულია φ-ზე φ≠π/2, შემდეგ φ→α tan φ → tan α და, შესაბამისად, ტანგენტის დახრილობა იქნება:

იმათ. f" (x)= tg α .

ამრიგად, გეომეტრიულად y" (x 0)წარმოადგენს ამ ფუნქციის გრაფიკის ტანგენტის დახრილობას წერტილში x 0, ე.ი. მოცემული არგუმენტის მნიშვნელობისთვის x, წარმოებული უდრის ფუნქციის გრაფიკზე ტანგენტის მიერ წარმოქმნილი კუთხის ტანგენტს f(x)შესაბამის წერტილში M 0 (x; y)დადებითი ღერძის მიმართულებით ოქსი.

მაგალითი.იპოვეთ მრუდის ტანგენსის დახრილობა y = x 2 წერტილში მ(-1; 1).

ჩვენ უკვე ვნახეთ, რომ ( x 2)" = 2X. მაგრამ მრუდის ტანგენსის კუთხური კოეფიციენტი არის tan α = წ"| x=-1 = – 2.

ფუნქციების განსხვავებულობა. დიფერენციალური ფუნქციის უწყვეტობა

ფუნქცია y=f(x)დაურეკა დიფერენცირებადირაღაც მომენტში x 0 თუ მას აქვს გარკვეული წარმოებული ამ ეტაპზე, ე.ი. თუ ურთიერთობის ზღვარი არსებობს და სასრულია.

თუ ფუნქცია დიფერენცირებადია გარკვეული სეგმენტის თითოეულ წერტილში [ ა; ბ] ან ინტერვალი ( ა; ბ), შემდეგ ამბობენ, რომ ის დიფერენცირებადისეგმენტზე [ ა; ბ] ან, შესაბამისად, ინტერვალში ( ა; ბ).

მოქმედებს შემდეგი თეორემა, რომელიც ადგენს კავშირს დიფერენცირებად და უწყვეტ ფუნქციებს შორის.

თეორემა.თუ ფუნქცია y=f(x)რაღაც მომენტში დიფერენცირებადი x 0, მაშინ ის ამ ეტაპზე უწყვეტია.

ამრიგად, ფუნქციის დიფერენციალურობიდან გამომდინარეობს მისი უწყვეტობა.

მტკიცებულება. თუ , ეს

,

სადაც α არის უსასრულო სიდიდე, ე.ი. სიდიდე, რომელიც მიდრეკილია ნულისკენ, როგორც Δ x→0. Მაგრამ შემდეგ

Δ წ=ვ "(x 0) Δ x+αΔ x=> Δ წ→0 Δ-ზე x→0, ე.ი. f(x) – f(x 0)→0 საათზე x→x 0, რაც ნიშნავს, რომ ფუნქცია f(x)უწყვეტი წერტილში x 0 . ქ.ე.დ.

ამრიგად, ფუნქციას არ შეიძლება ჰქონდეს წარმოებული უწყვეტობის წერტილებში. საპირისპირო არ არის მართალი: არის უწყვეტი ფუნქციები, რომლებიც არ არის დიფერენცირებადი ზოგიერთ წერტილში (ანუ არ აქვთ წარმოებული ამ წერტილებში).

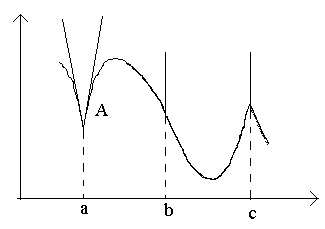
განვიხილოთ ფიგურაში მოცემული პუნქტები ა, ბ, გ.

წერტილში აΔ x→0 შეფარდებას არ აქვს ლიმიტი (რადგან ცალმხრივი ლიმიტები განსხვავებულია Δ-სთვის x→0–0 და Δ x→0+0). წერტილში აგრაფიკი არ არის განსაზღვრული ტანგენსი, მაგრამ არსებობს ორი განსხვავებული ცალმხრივი ტანგენსი დახრილობით რომ 1 და რომ 2. ამ ტიპის წერტილს კუთხის წერტილი ეწოდება.

წერტილში ბΔ x→0 თანაფარდობა არის მუდმივი ნიშანი უსასრულოდ დიდი რაოდენობით. ფუნქციას აქვს უსასრულო წარმოებული. ამ დროს გრაფიკს აქვს ვერტიკალური ტანგენსი. წერტილის ტიპი – ვერტიკალური ტანგენსის „შებრუნების წერტილი“.

წერტილში გცალმხრივი წარმოებულები არის სხვადასხვა ნიშნის უსასრულოდ დიდი რაოდენობა. ამ დროს გრაფიკს აქვს ორი შერწყმული ვერტიკალური ტანგენსი. ტიპი - "დაბრუნების წერტილი" ვერტიკალური ტანგენტით - კუთხის წერტილის განსაკუთრებული შემთხვევა.

ქვემოთ მოყვანილი ფიგურები გვიჩვენებს, თუ სად შეიძლება მიაღწიოს ფუნქციას უმცირეს და უდიდეს მნიშვნელობას. მარცხენა ფიგურაში უმცირესი და უდიდესი მნიშვნელობები ფიქსირდება ფუნქციის ლოკალური მინიმალური და მაქსიმუმის წერტილებზე. მარჯვენა სურათზე - სეგმენტის ბოლოებში.

თუ ფუნქცია წ = ვ(x) არის უწყვეტი ინტერვალზე [ ა, ბ] , შემდეგ ის აღწევს ამ სეგმენტზე სულ მცირე და უმაღლესი ღირებულებები . ეს, როგორც უკვე აღვნიშნეთ, შეიძლება მოხდეს ნებისმიერში ექსტრემალური წერტილები, ან სეგმენტის ბოლოებში. ამიტომ, რომ იპოვოთ სულ მცირე და ფუნქციის უდიდესი მნიშვნელობები , უწყვეტი ინტერვალზე [ ა, ბ] , თქვენ უნდა გამოთვალოთ მისი მნიშვნელობები ყველაში კრიტიკული წერტილებიდა სეგმენტის ბოლოებში და შემდეგ აირჩიე მათგან ყველაზე პატარა და უდიდესი.

მოდით, მაგალითად, გსურთ განსაზღვროთ ფუნქციის უდიდესი მნიშვნელობა ვ(x) სეგმენტზე [ ა, ბ] . ამისათვის თქვენ უნდა იპოვოთ მისი ყველა კრიტიკული წერტილი, რომელიც მდებარეობს [ ა, ბ] .

Კრიტიკული წერტილი ე.წ. წერტილი, სადაც ფუნქცია განსაზღვრულია, და ის წარმოებულიან ნულის ტოლია ან არ არსებობს. შემდეგ თქვენ უნდა გამოთვალოთ ფუნქციის მნიშვნელობები კრიტიკულ წერტილებში. და ბოლოს, უნდა შევადაროთ ფუნქციის მნიშვნელობა კრიტიკულ წერტილებში და სეგმენტის ბოლოებში ( ვ(ა) და ვ(ბ)). ამ რიცხვებიდან ყველაზე დიდი იქნება ფუნქციის უდიდესი მნიშვნელობა სეგმენტზე [ა, ბ] .

პოვნის პრობლემები ფუნქციის უმცირესი მნიშვნელობები .

ჩვენ ერთად ვეძებთ ფუნქციის უმცირეს და უდიდეს მნიშვნელობებს

მაგალითი 1. იპოვეთ ფუნქციის უმცირესი და უდიდესი მნიშვნელობები სეგმენტზე [-1, 2] .

გამოსავალი. იპოვეთ ამ ფუნქციის წარმოებული. წარმოებული გავუტოლოთ ნულს () და მივიღოთ ორი კრიტიკული წერტილი: და . მოცემულ სეგმენტზე ფუნქციის უმცირესი და უდიდესი მნიშვნელობების საპოვნელად საკმარისია მისი მნიშვნელობების გამოთვლა სეგმენტის ბოლოებში და წერტილში, რადგან წერტილი არ ეკუთვნის სეგმენტს [-1, 2]. ეს ფუნქციის მნიშვნელობებია: , , . Აქედან გამომდინარეობს, რომ ფუნქციის უმცირესი მნიშვნელობა(ქვემოთ გრაფიკზე მითითებული წითლად), ტოლია -7, მიიღწევა სეგმენტის მარჯვენა ბოლოს - წერტილში, და უდიდესი(გრაფიკაზე ასევე წითელი), უდრის 9, - კრიტიკულ წერტილში.

თუ ფუნქცია უწყვეტია გარკვეულ ინტერვალში და ეს ინტერვალი არ არის სეგმენტი (მაგრამ არის, მაგალითად, ინტერვალი; განსხვავება ინტერვალსა და სეგმენტს შორის: ინტერვალის სასაზღვრო წერტილები არ შედის ინტერვალში, მაგრამ სეგმენტის სასაზღვრო წერტილები შედის სეგმენტში), მაშინ ფუნქციის მნიშვნელობებს შორის შეიძლება არ იყოს ყველაზე პატარა და უდიდესი. მაგალითად, ქვემოთ მოცემულ ფიგურაში ნაჩვენები ფუნქცია უწყვეტია ]-∞, +∞[-ზე და არ აქვს უდიდესი მნიშვნელობა.

თუმცა, ნებისმიერი ინტერვალისთვის (დახურული, ღია ან უსასრულო), უწყვეტი ფუნქციების შემდეგი თვისება მართალია.

გამოთვლების დროს თვითშემოწმებისთვის შეგიძლიათ გამოიყენოთ ონლაინ წარმოებული კალკულატორი .

მაგალითი 4. იპოვეთ ფუნქციის უმცირესი და უდიდესი მნიშვნელობები სეგმენტზე [-1, 3] .

გამოსავალი. ჩვენ ვპოულობთ ამ ფუნქციის წარმოებულს, როგორც კოეფიციენტის წარმოებულს:

.

წარმოებულს ვატოლებთ ნულს, რაც გვაძლევს ერთ კრიტიკულ წერტილს: . ეკუთვნის სეგმენტს [-1, 3]. მოცემულ სეგმენტზე ფუნქციის უმცირესი და უდიდესი მნიშვნელობების საპოვნელად, ჩვენ ვპოულობთ მის მნიშვნელობებს სეგმენტის ბოლოებში და ნაპოვნი კრიტიკულ წერტილში:

მოდით შევადაროთ ეს ღირებულებები. დასკვნა: -5/13-ის ტოლია, წერტილში და უმაღლესი ღირებულებაუდრის 1 წერტილში.

ჩვენ ერთად ვაგრძელებთ ფუნქციის უმცირესი და უდიდესი მნიშვნელობების ძიებას

არიან მასწავლებლები, რომლებიც ფუნქციის უმცირესი და უდიდესი მნიშვნელობების პოვნის თემაზე არ აძლევენ მოსწავლეებს გადასაჭრელ მაგალითებს, რომლებიც უფრო რთულია, ვიდრე ახლახან განვიხილეთ, ანუ ისეთები, სადაც ფუნქცია არის მრავალწევრი ან წილადი, რომლის მრიცხველი და მნიშვნელი მრავალწევრია. მაგრამ ჩვენ არ შემოვიფარგლებით ასეთი მაგალითებით, რადგან მასწავლებლებს შორის არიან ისეთებიც, რომლებსაც სურთ აიძულონ მოსწავლეები სრულად იფიქრონ (წარმოებულთა ცხრილი). ამიტომ გამოყენებული იქნება ლოგარითმი და ტრიგონომეტრიული ფუნქცია.

მაგალითი 8. იპოვეთ ფუნქციის უმცირესი და უდიდესი მნიშვნელობები სეგმენტზე .

გამოსავალი. ამ ფუნქციის წარმოებულს ვპოულობთ როგორც პროდუქტის წარმოებული :

წარმოებულს ვატოლებთ ნულს, რომელიც იძლევა ერთ კრიტიკულ წერტილს: . ის მიეკუთვნება სეგმენტს. მოცემულ სეგმენტზე ფუნქციის უმცირესი და უდიდესი მნიშვნელობების საპოვნელად, ჩვენ ვპოულობთ მის მნიშვნელობებს სეგმენტის ბოლოებში და ნაპოვნი კრიტიკულ წერტილში:

ყველა მოქმედების შედეგი: ფუნქცია აღწევს მინიმალურ მნიშვნელობას 0-ის ტოლი, წერტილში და წერტილში და უმაღლესი ღირებულება, თანაბარი ე², წერტილში.

გამოთვლების დროს თვითშემოწმებისთვის შეგიძლიათ გამოიყენოთ ონლაინ წარმოებული კალკულატორი .

მაგალითი 9. იპოვეთ ფუნქციის უმცირესი და უდიდესი მნიშვნელობები სეგმენტზე .

გამოსავალი. იპოვეთ ამ ფუნქციის წარმოებული:

წარმოებულს ვატოლებთ ნულს:

ერთადერთი კრიტიკული წერტილი ეკუთვნის სეგმენტს. მოცემულ სეგმენტზე ფუნქციის უმცირესი და უდიდესი მნიშვნელობების საპოვნელად, ჩვენ ვპოულობთ მის მნიშვნელობებს სეგმენტის ბოლოებში და ნაპოვნი კრიტიკულ წერტილში:

დასკვნა: ფუნქცია აღწევს მინიმალურ მნიშვნელობას, ტოლია , წერტილში და უმაღლესი ღირებულება, თანაბარი , წერტილში .

გამოყენებული ექსტრემალური პრობლემების დროს, ფუნქციის უმცირესი (მაქსიმალური) მნიშვნელობების პოვნა, როგორც წესი, მიდის მინიმუმის (მაქსიმუმის) პოვნამდე. მაგრამ უფრო დიდი პრაქტიკული ინტერესი არ არის თავად მინიმუმები ან მაქსიმუმები, არამედ არგუმენტის ის მნიშვნელობები, რომლითაც ისინი მიიღწევა. გამოყენებული პრობლემების გადაჭრისას წარმოიქმნება დამატებითი სირთულე - ფუნქციების შედგენა, რომელიც აღწერს განსახილველ ფენომენს ან პროცესს.

მაგალითი 10. 4 ცალი ტევადობის ავზი, რომელსაც აქვს კვადრატული ფუძის მქონე პარალელეპიპედის ფორმა და ზემოდან ღია, უნდა იყოს დაკონსერვებული. რა ზომის უნდა იყოს ავზი ისე, რომ მის დასაფარად ყველაზე ნაკლები მასალა იყოს გამოყენებული?

გამოსავალი. დაე x- ბაზის მხარე, თ- ავზის სიმაღლე, ს- მისი ზედაპირის ფართობი საფარის გარეშე, ვ- მისი მოცულობა. ავზის ზედაპირის ფართობი გამოიხატება ფორმულით, ე.ი. არის ორი ცვლადის ფუნქცია. გამოხატოს სერთი ცვლადის ფუნქციად ვიყენებთ იმ ფაქტს, რომ , საიდან . ნაპოვნი გამონათქვამის ჩანაცვლება თფორმულაში შევიდა ს:

განვიხილოთ ეს ფუნქცია უკიდურესად. ის ყველგან არის განსაზღვრული და დიფერენცირებადი ]0, +∞[ და

.

წარმოებულს ვატოლებთ ნულს () და ვპოულობთ კრიტიკულ წერტილს. გარდა ამისა, როდესაც წარმოებული არ არსებობს, მაგრამ ეს მნიშვნელობა არ შედის განმარტების დომენში და, შესაბამისად, არ შეიძლება იყოს ექსტრემალური წერტილი. ასე რომ, ეს არის ერთადერთი კრიტიკული წერტილი. მოდით შევამოწმოთ ის ექსტრემის არსებობაზე მეორე საკმარისი ნიშნის გამოყენებით. ვიპოვოთ მეორე წარმოებული. როდესაც მეორე წარმოებული მეტია ნულზე (). ეს ნიშნავს, რომ როდესაც ფუნქცია მიაღწევს მინიმუმს . მას შემდეგ მინიმალური არის ამ ფუნქციის ერთადერთი უკიდურესი, ეს არის მისი ყველაზე მცირე მნიშვნელობა. ასე რომ, ავზის ფუძის მხარე უნდა იყოს 2 მ, ხოლო მისი სიმაღლე უნდა იყოს .

გამოთვლების დროს თვითშემოწმებისთვის შეგიძლიათ გამოიყენოთ

პრაქტიკული თვალსაზრისით, ყველაზე დიდი ინტერესი არის წარმოებულის გამოყენება ფუნქციის უდიდესი და უმცირესი მნიშვნელობების მოსაძებნად. რასთან არის ეს დაკავშირებული? მოგების მაქსიმიზაცია, ხარჯების მინიმიზაცია, აღჭურვილობის ოპტიმალური დატვირთვის დადგენა... სხვა სიტყვებით რომ ვთქვათ, ცხოვრების ბევრ სფეროში გვიწევს ზოგიერთი პარამეტრის ოპტიმიზაციის პრობლემების გადაჭრა. და ეს არის ფუნქციის უდიდესი და უმცირესი მნიშვნელობების პოვნის ამოცანები.

უნდა აღინიშნოს, რომ ფუნქციის უდიდეს და უმცირეს მნიშვნელობებს, როგორც წესი, ეძებენ გარკვეულ X ინტერვალზე, რომელიც არის ფუნქციის მთელი დომენი ან განმარტების დომენის ნაწილი. თავად X ინტერვალი შეიძლება იყოს სეგმენტი, ღია ინტერვალი , უსასრულო ინტერვალი.

ამ სტატიაში ვისაუბრებთ ერთი ცვლადის y=f(x) მკაფიოდ განსაზღვრული ფუნქციის უდიდესი და უმცირესი მნიშვნელობების პოვნაზე.

გვერდის ნავიგაცია.

ფუნქციის უდიდესი და უმცირესი მნიშვნელობა - განმარტებები, ილუსტრაციები.

მოკლედ გადავხედოთ ძირითად განმარტებებს.

ფუნქციის უდიდესი მნიშვნელობა რომ ვინმესთვის უთანასწორობა მართალია.

ფუნქციის უმცირესი მნიშვნელობა y=f(x) X ინტერვალზე ასეთ მნიშვნელობას უწოდებენ რომ ვინმესთვის უთანასწორობა მართალია.

ეს განმარტებები ინტუიციურია: ფუნქციის უდიდესი (უმცირესი) მნიშვნელობა არის ყველაზე დიდი (უმცირესი) მიღებული მნიშვნელობა აბსცისაზე განსახილველ ინტერვალზე.

სტაციონარული წერტილები- ეს არის არგუმენტის მნიშვნელობები, რომლის დროსაც ფუნქციის წარმოებული ხდება ნული.

რატომ გვჭირდება სტაციონარული წერტილები უდიდესი და უმცირესი მნიშვნელობების პოვნისას? ამ კითხვაზე პასუხს იძლევა ფერმას თეორემა. ამ თეორემიდან გამომდინარეობს, რომ თუ დიფერენცირებად ფუნქციას აქვს ექსტრემუმი (ადგილობრივი მინიმუმი ან ადგილობრივი მაქსიმუმი) რაღაც მომენტში, მაშინ ეს წერტილი სტაციონარულია. ამრიგად, ფუნქცია ხშირად იღებს თავის უდიდეს (უმცირეს) მნიშვნელობას X ინტერვალზე ამ ინტერვალიდან ერთ-ერთ სტაციონარულ წერტილში.

ასევე, ფუნქციას ხშირად შეუძლია მიიღოს თავისი უდიდესი და მინიმალური მნიშვნელობები იმ წერტილებში, რომლებშიც ამ ფუნქციის პირველი წარმოებული არ არსებობს და თავად ფუნქციაა განსაზღვრული.

მოდით დაუყოვნებლივ ვუპასუხოთ ერთ-ერთ ყველაზე გავრცელებულ კითხვას ამ თემაზე: „ყოველთვის შესაძლებელია თუ არა ფუნქციის უდიდესი (უმცირესი) მნიშვნელობის დადგენა“? არა ყოველთვის არა. ზოგჯერ X ინტერვალის საზღვრები ემთხვევა ფუნქციის განსაზღვრის დომენის საზღვრებს, ან X ინტერვალი უსასრულოა. და ზოგიერთმა ფუნქციამ უსასრულობაში და განსაზღვრების დომენის საზღვრებში შეიძლება მიიღოს როგორც უსასრულოდ დიდი, ასევე უსასრულოდ მცირე მნიშვნელობები. ამ შემთხვევაში, ფუნქციის უდიდეს და უმცირეს მნიშვნელობაზე ვერაფერს ვიტყვით.

სიცხადისთვის, ჩვენ მივცემთ გრაფიკულ ილუსტრაციას. შეხედეთ სურათებს და ბევრი რამ გაირკვევა.

სეგმენტზე

პირველ ფიგურაში ფუნქცია იღებს უდიდეს (max y) და უმცირეს (min y) მნიშვნელობებს სეგმენტის შიგნით მდებარე სტაციონარულ წერტილებში [-6;6].

განვიხილოთ მეორე ფიგურაში ასახული შემთხვევა. მოდით შევცვალოთ სეგმენტი . ამ მაგალითში ფუნქციის უმცირესი მნიშვნელობა მიიღწევა სტაციონარულ წერტილში, ხოლო უდიდესი აბსცისის წერტილში, რომელიც შეესაბამება ინტერვალის მარჯვენა საზღვარს.

მე-3 სურათზე [-3;2] სეგმენტის სასაზღვრო წერტილები არის ფუნქციის უდიდესი და უმცირესი მნიშვნელობის შესაბამისი წერტილების აბსციები.

ღია ინტერვალზე

მეოთხე ფიგურაში ფუნქცია იღებს უდიდეს (max y) და უმცირეს (min y) მნიშვნელობებს ღია ინტერვალის შიგნით მდებარე სტაციონარულ წერტილებში (-6;6).

ინტერვალზე არ შეიძლება დასკვნის გაკეთება ყველაზე დიდი მნიშვნელობის შესახებ.

უსასრულობაში

მეშვიდე ფიგურაში წარმოდგენილ მაგალითში ფუნქცია იღებს უდიდეს მნიშვნელობას (max y) აბსცისის x=1 სტაციონარული წერტილით, ხოლო უმცირესი მნიშვნელობა (min y) მიიღწევა ინტერვალის მარჯვენა საზღვარზე. მინუს უსასრულობაში, ფუნქციის მნიშვნელობები ასიმპტომურად უახლოვდება y=3.

ინტერვალის მანძილზე ფუნქცია არ აღწევს არც უმცირეს და არც უდიდეს მნიშვნელობას. როდესაც x=2 მარჯვნიდან უახლოვდება, ფუნქციის მნიშვნელობები მიდრეკილია მინუს უსასრულობამდე (ხაზი x=2 არის ვერტიკალური ასიმპტოტი), და რადგან აბსცისა მიდრეკილია პლუს უსასრულობისკენ, ფუნქციის მნიშვნელობები ასიმპტომურად უახლოვდება y=3. ამ მაგალითის გრაფიკული ილუსტრაცია ნაჩვენებია 8-ში.

სეგმენტზე უწყვეტი ფუნქციის უდიდესი და უმცირესი მნიშვნელობების პოვნის ალგორითმი.

მოდით დავწეროთ ალგორითმი, რომელიც საშუალებას გვაძლევს ვიპოვოთ ფუნქციის უდიდესი და უმცირესი მნიშვნელობები სეგმენტზე.

1. ჩვენ ვპოულობთ ფუნქციის განსაზღვრის დომენს და ვამოწმებთ შეიცავს თუ არა ის მთელ სეგმენტს.
2. ჩვენ ვპოულობთ ყველა წერტილს, რომლებშიც პირველი წარმოებული არ არსებობს და რომლებიც შეიცავს სეგმენტს (ჩვეულებრივ, ასეთი წერტილები გვხვდება ფუნქციებში არგუმენტით მოდულის ნიშნით და სიმძლავრის ფუნქციებში წილად-რაციონალური მაჩვენებლით). თუ ასეთი პუნქტები არ არის, გადადით შემდეგ პუნქტზე.
3. ჩვენ ვადგენთ ყველა სტაციონალურ წერტილს, რომელიც შედის სეგმენტში. ამისათვის ვატოლებთ მას ნულს, ვხსნით მიღებულ განტოლებას და ვირჩევთ შესაფერის ფესვებს. თუ არ არის სტაციონარული წერტილები ან არცერთი მათგანი არ მოხვდება სეგმენტში, გადადით შემდეგ წერტილზე.
4. ჩვენ ვიანგარიშებთ ფუნქციის მნიშვნელობებს შერჩეულ სტაციონალურ წერტილებზე (ასეთის არსებობის შემთხვევაში), იმ წერტილებზე, რომლებშიც პირველი წარმოებული არ არსებობს (ასეთის არსებობის შემთხვევაში), ასევე x=a და x=b.
5. ფუნქციის მიღებული მნიშვნელობებიდან ვირჩევთ უდიდეს და უმცირესს - ისინი იქნება ფუნქციის საჭირო უდიდესი და უმცირესი მნიშვნელობები, შესაბამისად.

მოდით გავაანალიზოთ მაგალითის ამოხსნის ალგორითმი, რათა ვიპოვოთ ფუნქციის უდიდესი და უმცირესი მნიშვნელობები სეგმენტზე.

მაგალითი.

იპოვეთ ფუნქციის უდიდესი და უმცირესი მნიშვნელობა

• სეგმენტზე;
• სეგმენტზე [-4;-1].

გამოსავალი.

ფუნქციის განსაზღვრის დომენი არის რეალური რიცხვების მთელი ნაკრები, გარდა ნულისა, ანუ. ორივე სეგმენტი შედის განმარტების დომენში.

იპოვეთ ფუნქციის წარმოებული:

ცხადია, ფუნქციის წარმოებული არსებობს სეგმენტების ყველა წერტილში და [-4;-1].

განტოლებიდან განვსაზღვრავთ უძრავ წერტილებს. ერთადერთი რეალური ფესვი არის x=2. ეს სტაციონარული წერტილი ხვდება პირველ სეგმენტში.

პირველ შემთხვევაში, ჩვენ ვიანგარიშებთ ფუნქციის მნიშვნელობებს სეგმენტის ბოლოებში და სტაციონარულ წერტილში, ანუ x=1, x=2 და x=4:

აქედან გამომდინარე, ფუნქციის უდიდესი მნიშვნელობა მიიღწევა x=1-ზე და ყველაზე მცირე მნიშვნელობაზე – x=2-ზე.

მეორე შემთხვევაში, ჩვენ ვიანგარიშებთ ფუნქციის მნიშვნელობებს მხოლოდ სეგმენტის ბოლოებში [-4;-1] (რადგან ის არ შეიცავს ერთ სტაციონალურ წერტილს):

გამოსავალი.

დავიწყოთ ფუნქციის დომენით. წილადის მნიშვნელში კვადრატული ტრინომი არ უნდა გაქრეს:

ადვილია იმის შემოწმება, რომ პრობლემის განცხადებიდან ყველა ინტერვალი ეკუთვნის ფუნქციის განსაზღვრის სფეროს.

მოდით განვასხვავოთ ფუნქცია:

ცხადია, წარმოებული არსებობს ფუნქციის განსაზღვრის მთელ დომენში.

მოდი ვიპოვოთ სტაციონარული წერტილები. წარმოებული მიდის ნულზე ზე. ეს სტაციონარული წერტილი ხვდება (-3;1] და (-3;2) ინტერვალებში.

ახლა თქვენ შეგიძლიათ შეადაროთ თითოეულ წერტილში მიღებული შედეგები ფუნქციის გრაფიკს. ლურჯი წერტილოვანი ხაზები მიუთითებს ასიმპტოტებზე.

ამ ეტაპზე ჩვენ შეგვიძლია დავასრულოთ ფუნქციის უდიდესი და უმცირესი მნიშვნელობების პოვნა. ამ სტატიაში განხილული ალგორითმები საშუალებას გაძლევთ მიიღოთ შედეგები მინიმალური მოქმედებებით. თუმცა, შეიძლება სასარგებლო იყოს ჯერ განსაზღვროთ ფუნქციის გაზრდისა და შემცირების ინტერვალები და მხოლოდ ამის შემდეგ გამოვიტანოთ დასკვნები ფუნქციის უდიდესი და უმცირესი მნიშვნელობების შესახებ ნებისმიერ ინტერვალზე. ეს იძლევა უფრო მკაფიო სურათს და შედეგების მკაცრ დასაბუთებას.

განმარტება3 . 3 მოდით იყოს რაიმე ფუნქცია, მისი განმარტების დომენი და რაღაც (ღია) ინტერვალი (შესაძლოა და/ან) 7 . დავუძახოთ ფუნქცია უწყვეტი ინტერვალზე, თუ უწყვეტი ნებისმიერ წერტილში, ანუ ნებისმიერი არსებობს (შემოკლებით:

მოდით ახლა იყოს (დახურული) სეგმენტი . დავუძახოთ ფუნქცია უწყვეტი სეგმენტზე, თუ უწყვეტი ინტერვალზე, უწყვეტი მარჯვნივ წერტილში და უწყვეტი მარცხნივ წერტილში, ე.ი

მაგალითი3 . 13 განიხილეთ ფუნქცია (Heaviside ფუნქცია) სეგმენტზე , . შემდეგ ის უწყვეტია სეგმენტზე (მიუხედავად იმისა, რომ ამ წერტილში მას აქვს პირველი სახის შეწყვეტა).

ნახ. 3.15 ჰევისაიდის ფუნქციის გრაფიკი

მსგავსი განმარტება შეიძლება მიენიჭოს ფორმის ნახევარ ინტერვალებს და , მათ შორის შემთხვევებს და . თუმცა, ჩვენ შეგვიძლია განვაზოგადოთ ეს განმარტება თვითნებური ქვესიმრავლის შემთხვევაში შემდეგნაირად. ჯერ წარმოვიდგინოთ კონცეფცია გამოწვეულიფუძემდე: მოდით იყოს ფუძე, რომლის ყველა დაბოლოებას აქვს არა ცარიელი კვეთები . მოდით აღვნიშნოთ და განვიხილოთ ყველა სიმრავლე. ამის შემდეგ ადვილია კომპლექტის შემოწმება იქნება საფუძველი. ამრიგად, , და , სადაც , და არის წერტილის არაპუნქციური ორმხრივი (მარცხნივ, მარჯვნივ, შესაბამისად) უბნების ფუძეები (იხილეთ მათი განმარტება მიმდინარე თავის დასაწყისში).

განმარტება3 . 4 დავუძახოთ ფუნქცია უწყვეტი გადასაღებ მოედანზე, თუ

ადვილი მისახვედრია, რომ მაშინ და ამ განსაზღვრებაში ემთხვევა ზემოთ მოცემულს სპეციალურად ინტერვალისა და სეგმენტისთვის.

შეგახსენებთ, რომ ყველა ელემენტარული ფუნქცია უწყვეტია მათი განსაზღვრის სფეროების ყველა წერტილში და, შესაბამისად, უწყვეტია ნებისმიერ ინტერვალებსა და სეგმენტებზე, რომლებიც დევს მათ განსაზღვრების დომენებში.

ვინაიდან უწყვეტობა ინტერვალზე და სეგმენტზე არის განსაზღვრული წერტილით, თეორემა მოქმედებს, რაც თეორემა 3.1-ის უშუალო შედეგია:

თეორემა3 . 5 დაე და -- ფუნქციები და -- ინტერვალი ან სეგმენტი დევს . დაე და უწყვეტი ამისთვის . შემდეგ ფუნქციები , , უწყვეტი ამისთვის . თუ დამატებით ყველას თვალწინ , შემდეგ ფუნქცია ასევე უწყვეტია .

შემდეგი განცხადება გამომდინარეობს ამ თეორემიდან, ისევე როგორც თეორემიდან 3.1 - წინადადება 3.3:

შეთავაზება3 . 4 Რამოდენიმე ყველა ფუნქცია უწყვეტია ინტერვალზე ან სეგმენტზე -- ეს არის წრფივი სივრცე:

უწყვეტი ფუნქციის უფრო რთული თვისება გამოიხატება შემდეგი თეორემით.

თეორემა3 . 6 (უწყვეტი ფუნქციის ფესვის შესახებ) დაუშვით ფუნქცია უწყვეტი სეგმენტზე , და და -- სხვადასხვა ნიშნების რაოდენობა. (დაზუსტებისთვის, ჩვენ ვივარაუდებთ, რომ , ა .) მაშინ არის მინიმუმ ერთი ასეთი მნიშვნელობა , Რა (ანუ არის ერთი ფესვი მაინც განტოლებები ).

მტკიცებულება. მოდით შევხედოთ სეგმენტის შუაში. მაშინ ეს ან, ან, ან. პირველ შემთხვევაში აღმოჩენილია ფესვი: ეს არის . დანარჩენ ორ შემთხვევაში განიხილეთ სეგმენტის ის ნაწილი, რომლის ბოლოებზეც ფუნქცია იღებს სხვადასხვა ნიშნის მნიშვნელობებს: შემთხვევაში ან შემთხვევაში. სეგმენტის არჩეულ ნახევარს აღვნიშნავთ და იგივე პროცედურას მივმართავთ: გავყოთ ორ ნაწილად და , სადაც , და ვიპოვოთ. ფესვის აღმოჩენის შემთხვევაში; იმ შემთხვევაში, თუ ჩვენ შემდგომ განვიხილავთ სეგმენტს , შემთხვევაში - სეგმენტი და ა.შ.

ნახ. 3.16 სეგმენტის ზედიზედ გაყოფა შუაზე

ჩვენ ვიღებთ, რომ ან რომელიმე ეტაპზე აღმოჩნდება ფესვი, ან აშენდება წყობილი სეგმენტების სისტემა

რომელშიც ყოველი მომდევნო სეგმენტი წინას ნახევრად გრძელია. თანმიმდევრობა არ არის კლებადი და შემოსაზღვრულია ზემოდან (მაგალითად, რიცხვით); ამიტომ (თეორემა 2.13) მას აქვს ზღვარი. ქვემიმდევრობა - არამზარდი და ქვემოდან შემოსაზღვრული (მაგალითად, რიცხვით); ეს ნიშნავს, რომ არსებობს ზღვარი. ვინაიდან სეგმენტების სიგრძეები ქმნიან კლებად გეომეტრიულ პროგრესიას (მნიშვნელით), ისინი მიდრეკილნი არიან 0-მდე და ეს არის . მოდი ახლა დავაყენოთ. მერე

და

ვინაიდან ფუნქცია უწყვეტია. თუმცა, და , და , მიმდევრობების აგებით ისე, რომ უტოლობაში ზღვარზე გადასვლის თეორემით (თეორემა 2.7), და, ანუ და. ეს ნიშნავს, რომ და არის განტოლების ფესვი.

მაგალითი3 . 14 განიხილეთ ფუნქცია სეგმენტზე. ვინაიდან და არის სხვადასხვა ნიშნის რიცხვი, ფუნქცია 0-ზე გადადის ინტერვალის რაღაც მომენტში. ეს ნიშნავს, რომ განტოლებას აქვს ფესვი.

ნახ. 3.17 განტოლების ფესვის გრაფიკული გამოსახულება

დადასტურებული თეორემა რეალურად გვაძლევს საშუალებას ვიპოვოთ ფესვი, ყოველ შემთხვევაში, მიახლოებითი, წინასწარ განსაზღვრული სიზუსტის ნებისმიერი ხარისხით. ეს არის სეგმენტის ნახევრად გაყოფის მეთოდი, რომელიც აღწერილია თეორემის მტკიცებულებაში. ფესვის დაახლოებით პოვნის ამ და სხვა, უფრო ეფექტურ მეთოდებს უფრო დეტალურად გავეცნობით ქვემოთ, მას შემდეგ რაც შევისწავლით წარმოებულის ცნებას და თვისებებს.

გაითვალისწინეთ, რომ თეორემა არ ამბობს, რომ თუ მისი პირობები დაკმაყოფილებულია, მაშინ ფესვი უნიკალურია. როგორც ქვემოთ მოყვანილი სურათიდან ჩანს, შეიძლება იყოს ერთზე მეტი ფესვი (სურათზე არის 3).

ნახ. 3.18 ფუნქციის რამდენიმე ფესვი, რომელიც იღებს სხვადასხვა ნიშნის მნიშვნელობებს სეგმენტის ბოლოებში

ამასთან, თუ ფუნქცია მონოტონურად იზრდება ან მონოტონურად მცირდება სეგმენტზე, რომლის ბოლოებში იგი იღებს სხვადასხვა ნიშნის მნიშვნელობებს, მაშინ ფესვი უნიკალურია, რადგან მკაცრად ერთფეროვანი ფუნქცია იღებს მის თითოეულ მნიშვნელობას ზუსტად ერთ წერტილში. , მნიშვნელობის 0 ჩათვლით.

ნახ. 3.19 ერთფეროვან ფუნქციას არ შეიძლება ჰქონდეს ერთზე მეტი ფესვი

უწყვეტი ფუნქციის ფესვზე თეორემის უშუალო შედეგია შემდეგი თეორემა, რომელიც თავისთავად ძალიან მნიშვნელოვანია მათემატიკური ანალიზისას.

თეორემა3 . 7 (უწყვეტი ფუნქციის შუალედური მნიშვნელობის შესახებ) დაუშვით ფუნქცია უწყვეტი სეგმენტზე და (დაზუსტებისთვის ჩვენ ვივარაუდებთ, რომ ). დაე -- რაღაც რიცხვი დევს შორის და . მაშინ არის ასეთი წერტილი , Რა .

ნახ. 3.20 უწყვეტი ფუნქცია იღებს ნებისმიერ შუალედურ მნიშვნელობას

მტკიცებულება. განვიხილოთ დამხმარე ფუნქცია , სად . მერე და . ფუნქცია აშკარად უწყვეტია და წინა თეორემით არის ისეთი წერტილი, რომ . მაგრამ ეს თანასწორობა ნიშნავს იმას.

გაითვალისწინეთ, რომ თუ ფუნქცია არ არის უწყვეტი, მაშინ მან შეიძლება არ მიიღოს ყველა შუალედური მნიშვნელობა. მაგალითად, Heaviside ფუნქცია (იხ. მაგალითი 3.13) იღებს მნიშვნელობებს, მაგრამ არსად, მათ შორის ინტერვალში, არ იღებს, ვთქვათ, შუალედურ მნიშვნელობას. ფაქტია, რომ Heaviside ფუნქციას აქვს შეწყვეტა ზუსტად ინტერვალში მდებარე წერტილში.

ინტერვალზე უწყვეტი ფუნქციების თვისებების შემდგომი შესასწავლად დაგვჭირდება ნამდვილ რიცხვთა სისტემის შემდეგი დახვეწილი თვისება (ეს უკვე აღვნიშნეთ მე-2 თავში მონოტონურად მზარდი შეზღუდული ფუნქციის ლიმიტის თეორემასთან დაკავშირებით): ქვემოთ შემოსაზღვრული ნებისმიერი სიმრავლე (ანუ ისეთი, რომ ყველასთვის და ზოგიერთი რიცხვისთვის იწოდება ქვედა კიდეკომპლექტები) ხელმისაწვდომია ზუსტი ქვედა ზღვარი, ანუ ყველაზე დიდი რიცხვებიდან ისეთი რომ ყველასთვის . ანალოგიურად, თუ ნაკრები ზემოთ არის შემოსაზღვრული, მაშინ მას აქვს ზუსტი ზედა ზღვარი: ეს არის ყველაზე პატარა ზედა სახეები(რისთვისაც ყველასთვის).

ნახ. 3.21 შემოსაზღვრული ნაკრების ქვედა და ზედა საზღვრები

თუ , მაშინ არის წერტილების არ მზარდი თანმიმდევრობა, რომელიც მიდრეკილია . ანალოგიურად, თუ , მაშინ არის წერტილების შეუმცირებელი თანმიმდევრობა, რომელიც მიდრეკილია .

თუ წერტილი ეკუთვნის სიმრავლეს, მაშინ ეს არის ამ სიმრავლის უმცირესი ელემენტი: ; ანალოგიურად, თუ , რომ .

გარდა ამისა, შემდგომისთვის დაგვჭირდება შემდეგი

ლემა3 . 1 დაე -- უწყვეტი ფუნქცია სეგმენტზე და ბევრი იმ წერტილებს , რომელშიც (ან , ან ) არ არის ცარიელი. მერე უხვად არის უმცირესი ღირებულება , ისეთივე როგორც ყველას თვალწინ .

ნახ. 3.22 ყველაზე პატარა არგუმენტი, რომლის დროსაც ფუნქცია იღებს მითითებულ მნიშვნელობას

მტკიცებულება. ვინაიდან ეს არის შემოსაზღვრული ნაკრები (ის სეგმენტის ნაწილია), მას აქვს ინფიმუმი. მაშინ არსებობს არამზარდი თანმიმდევრობა , , ისეთი რომ . უფრო მეტიც, კომპლექტის განმარტებით. ამიტომ, ზღვარზე გადასვლისას, ჩვენ ვიღებთ, ერთი მხრივ,

და მეორეს მხრივ, ფუნქციის უწყვეტობის გამო,

ეს ნიშნავს , რომ წერტილი ეკუთვნის სიმრავლეს და .

იმ შემთხვევაში, როდესაც სიმრავლე განისაზღვრება უტოლობით, გვაქვს ყველასთვის და უტოლობაში ზღვრამდე გადასვლის თეორემა გვაქვს.

საიდან , რაც იმას ნიშნავს რომ და . ანალოგიურად, უთანასწორობის შემთხვევაში, უტოლობაში ზღვარზე გადასვლა იძლევა

საიდან და .

თეორემა3 . 8 (უწყვეტი ფუნქციის შეზღუდვის შესახებ) დაუშვით ფუნქცია უწყვეტი სეგმენტზე . მერე შეზღუდული , ანუ არის ასეთი მუდმივი , Რა ყველას თვალწინ .

ნახ. 3.23 სეგმენტზე უწყვეტი ფუნქცია შემოსაზღვრულია

მტკიცებულება. დავუშვათ საპირისპირო: არ იყოს შეზღუდული, მაგალითად, ზემოდან. მაშინ ყველა კომპლექტი , , , არ არის ცარიელი. წინა ლემის მიხედვით, თითოეულ ამ კომპლექტს აქვს ყველაზე მცირე მნიშვნელობა, . ეს ვაჩვენოთ

მართლა, . თუ რომელიმე წერტილი, მაგალითად, არის და შორის, მაშინ

ანუ შუალედური მნიშვნელობა და . ეს ნიშნავს, რომ უწყვეტი ფუნქციის შუალედური მნიშვნელობის შესახებ თეორემა არის ისეთი წერტილი, რომ , და . მაგრამ, იმის საპირისპიროდ, რომ - სიმრავლის უმცირესი მნიშვნელობა. აქედან გამომდინარეობს, რომ ყველასთვის.

ანალოგიურად, შემდგომში დამტკიცებულია, რომ ყველასთვის, ყველასთვის და ა.შ. ასე რომ, მზარდი თანმიმდევრობა შემოსაზღვრულია ზემოთ რიცხვით. ამიტომ ის არსებობს. ფუნქციის უწყვეტობიდან გამომდინარეობს, რომ არსებობს , მაგრამ ზე, ასე რომ არ არის ლიმიტი. შედეგად მიღებული წინააღმდეგობა ადასტურებს, რომ ფუნქცია შემოსაზღვრულია ზემოთ.

ანალოგიურად დასტურდება, რომ იგი შემოსაზღვრულია ქვემოდან, რაც გულისხმობს თეორემის დებულებას.

ცხადია, შეუძლებელია თეორემის პირობების შესუსტება: თუ ფუნქცია არ არის უწყვეტი, მაშინ ის არ უნდა იყოს შემოსაზღვრული ინტერვალზე (მაგალითად ვაძლევთ ფუნქციას

სეგმენტზე. ეს ფუნქცია არ არის შემოსაზღვრული ინტერვალით, რადგან at აქვს მეორე სახის შეწყვეტის წერტილი, ისეთი, რომ ზე. ასევე შეუძლებელია თეორემის მდგომარეობაში სეგმენტის ჩანაცვლება ინტერვალით ან ნახევარინტერვალით: მაგალითად, განიხილეთ იგივე ფუნქცია ნახევარ ინტერვალზე. ფუნქცია უწყვეტია ამ ნახევარ ინტერვალზე, მაგრამ შეუზღუდავია, იმის გამო, რომ .

საუკეთესო მუდმივების პოვნა, რომლებიც შეიძლება გამოყენებულ იქნას ფუნქციის ზემოდან და ქვემოდან მოცემულ ინტერვალზე შესაზღუდად, ბუნებრივად მიგვიყვანს ამ ინტერვალზე უწყვეტი ფუნქციის მინიმალური და მაქსიმუმის პოვნის პრობლემამდე. ამ პრობლემის გადაჭრის შესაძლებლობა აღწერილია შემდეგი თეორემით.

თეორემა3 . 9 (უკიდურობის მიღწევის შესახებ უწყვეტი ფუნქციით) დაუშვით ფუნქცია უწყვეტი სეგმენტზე . მაშინ არის წერტილი , ისეთივე როგორც ყველას თვალწინ (ანუ -- მინიმალური ქულა: ), და არის წერტილი , ისეთივე როგორც ყველას თვალწინ (ანუ -- მაქსიმალური ქულა: ). სხვა სიტყვებით რომ ვთქვათ, მინიმალური და მაქსიმალური 8 სეგმენტზე უწყვეტი ფუნქციის მნიშვნელობები არსებობს და მიიღწევა ზოგიერთ წერტილში და ამ სეგმენტს.

ნახ. 3.24 სეგმენტზე უწყვეტი ფუნქცია აღწევს მაქსიმუმს და მინიმუმს

მტკიცებულება. ვინაიდან, წინა თეორემის მიხედვით, ფუნქცია შემოსაზღვრულია ზემოდან, მაშინ ფუნქციის მნიშვნელობებისთვის არის ზუსტი ზედა ზღვარი -- რიცხვით. . ამრიგად, სიმრავლეები ,..., ,..., არ არის ცარიელი და წინა ლემის მიხედვით ისინი შეიცავს უმცირეს მნიშვნელობებს: , . ისინი არ მცირდება (ეს განცხადება დადასტურებულია ზუსტად ისევე, როგორც წინა თეორემაში):

და შემოიფარგლება ზემოდან . მაშასადამე, მონოტონური შემოსაზღვრული მიმდევრობის ზღვრის შესახებ თეორემით არსებობს ზღვარი Since , მაშინ

უთანასწორობაში ზღვარზე გადასვლის თეორემით, ანუ . მაგრამ ყველასთან, მათ შორის. აქედან გამოდის, რომ, ანუ ფუნქციის მაქსიმუმი მიიღწევა წერტილში.

მინიმალური ქულის არსებობა ანალოგიურად დასტურდება.

ამ თეორემაში, ისევე როგორც წინაში, შეუძლებელია პირობების შესუსტება: თუ ფუნქცია არ არის უწყვეტი, მაშინ მან შეიძლება ვერ მიაღწიოს თავის მაქსიმალურ ან მინიმალურ მნიშვნელობას სეგმენტზე, თუნდაც ის შეზღუდული იყოს. მაგალითად, ავიღოთ ფუნქცია

სეგმენტზე. ეს ფუნქცია შემოსაზღვრულია ინტერვალზე (ცხადია) და , თუმცა, ის არ იღებს მნიშვნელობას 1 სეგმენტის არცერთ წერტილში (გაითვალისწინეთ, რომ და არა 1). ფაქტია, რომ ამ ფუნქციას აქვს პირველი ტიპის უწყვეტობა წერტილში , ასე რომ ლიმიტი არ არის 0 წერტილში ფუნქციის მნიშვნელობის ტოლი. გარდა ამისა, უწყვეტი ფუნქცია განსაზღვრულია ინტერვალზე ან სხვა სიმრავლეზე, რომელიც არ არის დახურულ სეგმენტს (ნახევარ ინტერვალზე, ნახევრად ღერძზე) ასევე არ შეუძლია მიიღოს უკიდურესი მნიშვნელობები. მაგალითად, განიხილეთ ფუნქცია ინტერვალზე. აშკარაა, რომ ფუნქცია უწყვეტია და, თუმცა, ფუნქცია არ იღებს არც მნიშვნელობას 0 და არც მნიშვნელობას 1 ინტერვალის ნებისმიერ წერტილში. განვიხილოთ ფუნქციაც ღერძის ლილვზე. ეს ფუნქცია უწყვეტია, იზრდება, იღებს მის მინიმალურ მნიშვნელობას 0 წერტილში, მაგრამ არ იღებს მაქსიმალურ მნიშვნელობას ნებისმიერ წერტილში (თუმცა ზემოდან შემოიფარგლება რიცხვით და

განმარტება. თუ ფუნქცია ვ(x) განისაზღვრება ინტერვალზე [ ა, ბ], არის უწყვეტი ინტერვალის თითოეულ წერტილში ( ა, ბ), წერტილში აუწყვეტი მარჯვნივ, წერტილში ბარის უწყვეტი მარცხნივ, მაშინ ვამბობთ, რომ ფუნქცია ვ(x) უწყვეტი სეგმენტზე [ა, ბ].

სხვა სიტყვებით რომ ვთქვათ, ფუნქცია ვ(x) არის უწყვეტი ინტერვალზე [ ა, ბ], თუ დაკმაყოფილებულია სამი პირობა:

1) "x 0 Î( ა, ბ): ვ(x) = ვ(x 0);

2) ვ(x) = ვ(ა);

3) ვ(x) = ვ(ბ).

ფუნქციებისთვის, რომლებიც უწყვეტია ინტერვალზე, განვიხილავთ ზოგიერთ თვისებას, რომელსაც ვაყალიბებთ შემდეგი თეორემების სახით, მტკიცებულებების განხორციელების გარეშე.

თეორემა 1. თუ ფუნქცია ვ(x) არის უწყვეტი ინტერვალზე [ ა, ბ], შემდეგ ის აღწევს თავის მინიმალურ და მაქსიმალურ მნიშვნელობებს ამ სეგმენტზე.

ეს თეორემა აცხადებს (ნახ. 1.15), რომ სეგმენტზე [ ა, ბ] არის ასეთი წერტილი x 1 რომ ვ(x 1) £ ვ(x) ნებისმიერისთვის xდან [ ა, ბ] და რომ არსებობს წერტილი x 2 (x 2 О[ ა, ბ]) ისეთივე როგორც " xÎ[ ა, ბ] (ვ(x 2)³ ვ(x)).

მნიშვნელობა ვ(x 1) არის უდიდესი მოცემული ფუნქციისთვის [ ა, ბ], ა ვ(x 2) – ყველაზე პატარა. აღვნიშნოთ: ვ(x 1) = მ, ვ(x 2) =მ. ვინაიდან ამისთვის ვ(x) უტოლობა მოქმედებს: " xÎ[ ა, ბ] მ£ ვ(x) £ მ, შემდეგ მივიღებთ შემდეგ დასკვნას თეორემა 1-დან.

შედეგი. თუ ფუნქცია ვ(x) არის უწყვეტი ინტერვალზე, შემდეგ ის შემოიფარგლება ამ ინტერვალზე.

თეორემა 2. თუ ფუნქცია ვ(x) არის უწყვეტი ინტერვალზე [ ა, ბ] და იღებს სხვადასხვა ნიშნის მნიშვნელობებს სეგმენტის ბოლოებში, მაშინ არის ასეთი შიდა წერტილი x 0 სეგმენტი [ ა, ბ], რომელშიც ფუნქცია გადადის 0-ზე, ე.ი. $ x 0 Î ( ა, ბ) (ვ(x 0) = 0).

ეს თეორემა ამბობს, რომ ფუნქციის გრაფიკი y = ვ(x), უწყვეტი ინტერვალზე [ ა, ბ], კვეთს ღერძს ოქსიერთხელ მაინც თუ ღირებულებები ვ(ა) და ვ(ბ) აქვს საპირისპირო ნიშნები. ასე რომ, (ნახ. 1.16) ვ(ა) > 0, ვ(ბ) < 0 и функция ვ(x) წერტილებში ხდება 0 x 1 , x 2 , x 3 .

თეორემა 3. დაუშვით ფუნქცია ვ(x) არის უწყვეტი ინტერვალზე [ ა, ბ], ვ(ა) = ა, ვ(ბ) = ბდა ა¹ ბ. (სურ. 1.17). შემდეგ ნებისმიერი ნომრისთვის C, ჩასმულია ნომრებს შორის ადა ბ, არის ასეთი შინაგანი წერტილი x 0 სეგმენტი [ ა, ბ], Რა ვ(x 0) = C.

შედეგი. თუ ფუნქცია ვ(x) არის უწყვეტი ინტერვალზე [ ა, ბ], მ- უმცირესი ღირებულება ვ(x), მ- ფუნქციის უდიდესი მნიშვნელობა ვ(x) სეგმენტზე [ ა, ბ], მაშინ ფუნქცია იღებს (ერთხელ მაინც) ნებისმიერ მნიშვნელობას მშორის დადებული მდა მდა, შესაბამისად, სეგმენტი [ მ, მ] არის ყველა ფუნქციის მნიშვნელობების ნაკრები ვ(x) სეგმენტზე [ ა, ბ].

გაითვალისწინეთ, რომ თუ ფუნქცია უწყვეტია ინტერვალზე ( ა, ბ) ან აქვს სეგმენტზე [ ა, ბ] შეწყვეტის წერტილები, შემდეგ თეორემები 1, 2, 3 ასეთი ფუნქციისთვის წყვეტს ჭეშმარიტებას.

დასასრულს, განიხილეთ თეორემა შებრუნებული ფუნქციის არსებობის შესახებ.

თეორემა 4. დაე ვ(x) არის უწყვეტი ინტერვალზე X, იზრდება (ან მცირდება) მიერ Xდა აქვს მნიშვნელობების სპექტრი ი. შემდეგ ფუნქციისთვის y = ვ(x) არის შებრუნებული ფუნქცია x= ჯ(წ), განსაზღვრულია ინტერვალზე ი, უწყვეტი და მზარდი (ან კლებადი) მიერ იმრავალი მნიშვნელობით X.

კომენტარი. დაუშვით ფუნქცია x= ჯ(წ) არის ფუნქციის შებრუნებული ვ(x). ვინაიდან არგუმენტი ჩვეულებრივ აღინიშნება x, და ფუნქცია მეშვეობით წ, შემდეგ ვწერთ შებრუნებულ ფუნქციას ფორმაში y =ჯ(x).

მაგალითი 1. ფუნქცია y = x 2 (სურ. 1.8, ა) ნაკრებზე X= }