ორი მართკუთხა პულსის სპექტრი. მართკუთხა იმპულსების მიმდევრობის სპექტრული შემადგენლობა სხვადასხვა სამუშაო ციკლზე
ლიტერატურა: [L.1], გვ. 40
მაგალითად, ჩვენ ვაძლევთ ფურიეს სერიის გაფართოებას მართკუთხა იმპულსების პერიოდული მიმდევრობით ამპლიტუდით, ხანგრძლივობით და გამეორების პერიოდით, სიმეტრიული ნულის მიმართ, ე.ი.
 , (2.10)
, (2.10)
Აქ 
ასეთი სიგნალის გაფართოება ფურიეს სერიაში იძლევა
 , (2.11)
, (2.11)
სად არის სამუშაო ციკლი.
აღნიშვნის გასამარტივებლად, შეგიძლიათ შეიყვანოთ ნოტაცია
 , (2.12)
, (2.12)
შემდეგ (2.11) ჩაიწერება შემდეგნაირად
 , (2.13)
, (2.13)
ნახ. 2.3 გვიჩვენებს მართკუთხა იმპულსების თანმიმდევრობას. მიმდევრობის სპექტრი, ისევე როგორც ნებისმიერი სხვა პერიოდული სიგნალი, დისკრეტული (ხაზოვანი) ხასიათისაა.
სპექტრის გარსი (ნახ. 2.3, ბ) პროპორციულია  . სიხშირის ღერძის გასწვრივ მანძილი სპექტრის ორ მიმდებარე კომპონენტს შორის არის , ხოლო ორ ნულოვან მნიშვნელობას შორის (სპექტრის წილის სიგანე) არის . ჰარმონიული კომპონენტების რაოდენობა ერთ წილში, ფიგურაში მარჯვნივ ნულოვანი მნიშვნელობის ჩათვლით, არის , სადაც ნიშანი ნიშნავს დამრგვალებას უახლოეს მთელ რიცხვზე, ნაკლები (თუ სამუშაო ციკლი არის წილადი რიცხვი) ან (თუ მოვალეობის ციკლი არის მთელი მნიშვნელობა). როგორც პერიოდი იზრდება, ფუნდამენტური სიხშირე
. სიხშირის ღერძის გასწვრივ მანძილი სპექტრის ორ მიმდებარე კომპონენტს შორის არის , ხოლო ორ ნულოვან მნიშვნელობას შორის (სპექტრის წილის სიგანე) არის . ჰარმონიული კომპონენტების რაოდენობა ერთ წილში, ფიგურაში მარჯვნივ ნულოვანი მნიშვნელობის ჩათვლით, არის , სადაც ნიშანი ნიშნავს დამრგვალებას უახლოეს მთელ რიცხვზე, ნაკლები (თუ სამუშაო ციკლი არის წილადი რიცხვი) ან (თუ მოვალეობის ციკლი არის მთელი მნიშვნელობა). როგორც პერიოდი იზრდება, ფუნდამენტური სიხშირე  მცირდება, დიაგრამაში სპექტრული კომპონენტები უახლოვდება ერთმანეთს, მცირდება ჰარმონიის ამპლიტუდებიც. ამ შემთხვევაში კონვერტის ფორმა შენარჩუნებულია.
მცირდება, დიაგრამაში სპექტრული კომპონენტები უახლოვდება ერთმანეთს, მცირდება ჰარმონიის ამპლიტუდებიც. ამ შემთხვევაში კონვერტის ფორმა შენარჩუნებულია.




სპექტრალური ანალიზის პრაქტიკული ამოცანების გადაჭრისას კუთხური სიხშირეების ნაცვლად გამოიყენება ციკლური სიხშირეები.  , იზომება ჰერცში. ცხადია, დიაგრამაზე მიმდებარე ჰარმონიებს შორის მანძილი იქნება , ხოლო ერთი სპექტრის წილის სიგანე იქნება . ეს მნიშვნელობები მოცემულია დიაგრამაში ფრჩხილებში.
, იზომება ჰერცში. ცხადია, დიაგრამაზე მიმდებარე ჰარმონიებს შორის მანძილი იქნება , ხოლო ერთი სპექტრის წილის სიგანე იქნება . ეს მნიშვნელობები მოცემულია დიაგრამაში ფრჩხილებში.
პრაქტიკულ რადიოინჟინერიაში, უმეტეს შემთხვევაში, სპექტრული წარმოდგენის ნაცვლად (ნახ. 2.3, ბ) გამოიყენება ამპლიტუდის და ფაზის სპექტრის სპექტრული დიაგრამები. მართკუთხა იმპულსების თანმიმდევრობის ამპლიტუდის სპექტრი ნაჩვენებია ნახ. 2.3, გ.
ცხადია, ამპლიტუდის სპექტრის გარსი პროპორციულია  .
.
რაც შეეხება ფაზურ სპექტრს (ნახ. 2.3, დ), ითვლება, რომ ჰარმონიული კომპონენტების საწყისი ფაზები მკვეთრად იცვლება ოდენობით. -π როდესაც კონვერტის ნიშანი იცვლება sinc kπ/q. პირველი წილის ჰარმონიის საწყისი ფაზები ითვლება ნულამდე. შემდეგ იქნება მეორე წილის ჰარმონიის საწყისი ფაზები φ = -π , მესამე ფურცელი φ = -2πდა ა.შ.
განვიხილოთ სიგნალის კიდევ ერთი ფურიეს სერიის წარმოდგენა. ამისათვის ჩვენ ვიყენებთ ეილერის ფორმულას
 .
.
ამ ფორმულის შესაბამისად, ფურიეს სერიაში სიგნალის გაფართოების kth კომპონენტი (2.9) შეიძლება წარმოდგენილი იყოს შემდეგნაირად.
 ;
;  . (2.15)
. (2.15)
აქ რაოდენობები და არის რთული და წარმოადგენს სპექტრის კომპონენტების რთულ ამპლიტუდას. მერე სერია
ფურიე (2.8) (2.14) გათვალისწინებით მიიღებს შემდეგ ფორმას
 , (2.16)
, (2.16)
 , (2.17)
, (2.17)
ადვილია იმის შემოწმება, რომ გაფართოება (2.16) ხორციელდება საბაზისო ფუნქციების თვალსაზრისით  , რომლებიც ასევე ორთოგონალურია ინტერვალზე
, რომლებიც ასევე ორთოგონალურია ინტერვალზე  , ე.ი.
, ე.ი.

გამოხატულება (2.16) არის რთული ფორმაფურიეს სერია, რომელიც ვრცელდება უარყოფით სიხშირეებზე. რაოდენობები და  , სადაც აღნიშნავს სიდიდის რთულ კონიუგატს, ე.წ რთული ამპლიტუდებისპექტრი იმიტომ რომ არის რთული სიდიდე, აქედან გამომდინარეობს (2.15) რომ
, სადაც აღნიშნავს სიდიდის რთულ კონიუგატს, ე.წ რთული ამპლიტუდებისპექტრი იმიტომ რომ არის რთული სიდიდე, აქედან გამომდინარეობს (2.15) რომ
 და
და  .
.
მაშინ მთლიანობა შეადგენს ამპლიტუდის სპექტრს და მთლიანობა შეადგენს სიგნალის ფაზურ სპექტრს.

ნახ. ნახაზი 2.4 გვიჩვენებს ზემოთ განხილული მართკუთხა იმპულსების მიმდევრობის სპექტრის სპექტრულ დიაგრამას, რომელიც წარმოდგენილია რთული ფურიეს სერიით

სპექტრს ასევე აქვს ხაზის ხასიათი, მაგრამ განსხვავებით ადრე განხილული სპექტრებისგან, იგი განისაზღვრება როგორც დადებითი, ასევე უარყოფითი სიხშირეების რეგიონში. ვინაიდან ეს არგუმენტის ლუწი ფუნქციაა, სპექტრული დიაგრამა სიმეტრიულია ნულის მიმართ.
(2.15) საფუძველზე შეგვიძლია დავადგინოთ შესაბამისობა კოეფიციენტებსა და გაფართოებას შორის (2.3). იმიტომ რომ
 და
და  ,
,
შემდეგ შედეგად მივიღებთ
 . (2.18)
. (2.18)
გამონათქვამები (2.5) და (2.18) საშუალებას გაძლევთ იპოვოთ მნიშვნელობები პრაქტიკულ გამოთვლებში.
მოდით მივცეთ ფურიეს სერიის რთული ფორმის გეომეტრიული ინტერპრეტაცია. მოდით ავირჩიოთ სიგნალის სპექტრის kth კომპონენტი. რთული ფორმით, kth კომპონენტი აღწერილია ფორმულით
სადაც და განისაზღვრება გამონათქვამებით (2.15).
კომპლექსურ სიბრტყეში, (2.19) თითოეული ტერმინი წარმოდგენილია სიგრძის ვექტორებად  , ბრუნავს კუთხით და რეალურ ღერძთან შედარებით და ბრუნავს საპირისპირო მიმართულებით სიხშირით (ნახ. 2.5).
, ბრუნავს კუთხით და რეალურ ღერძთან შედარებით და ბრუნავს საპირისპირო მიმართულებით სიხშირით (ნახ. 2.5).
ცხადია, ამ ვექტორების ჯამი იძლევა ვექტორს, რომელიც მდებარეობს რეალურ ღერძზე, რომლის სიგრძეა . მაგრამ ეს ვექტორი შეესაბამება ჰარმონიულ კომპონენტს


რაც შეეხება ვექტორების პროგნოზებს წარმოსახვით ღერძზე, ამ პროექციებს აქვთ თანაბარი სიგრძე, მაგრამ საპირისპირო მიმართულებები და ჯამია ნულამდე. ეს ნიშნავს, რომ რთული ფორმით წარმოდგენილი სიგნალები (2.16) რეალურად რეალური სიგნალებია. სხვა სიტყვებით რომ ვთქვათ, ფურიეს სერიის რთული ფორმა არის მათემატიკურიაბსტრაქცია, რომელიც ძალიან მოსახერხებელია სპექტრული ანალიზის მთელი რიგი ამოცანების გადასაჭრელად. ამიტომ, ზოგჯერ ტრიგონომეტრიული ფურიეს სერიებით განსაზღვრულ სპექტრს უწოდებენ ფიზიკური სპექტრიდა ფურიეს სერიის რთული ფორმა არის მათემატიკური სპექტრი.
და დასასრულს, განვიხილავთ ენერგიისა და ენერგიის განაწილების საკითხს პერიოდული სიგნალის სპექტრში. ამისათვის ჩვენ ვიყენებთ პარსევალის ტოლობას (1.42). როდესაც სიგნალი გაფართოვდება ტრიგონომეტრიულ ფურიეს სერიაში, გამოხატულება (1.42) იღებს ფორმას.
 .
.
DC ენერგია
 ,
,
და kth ჰარმონიკის ენერგია
 .
.
შემდეგ სიგნალის ენერგია
 . (2.20)
. (2.20)
იმიტომ რომ სიგნალის საშუალო სიმძლავრე
 ,
,
შემდეგ (2.18) გათვალისწინებით
 . (2.21)
. (2.21)
როდესაც სიგნალი გაფართოვდება ფურიეს რთულ სერიებში, გამოხატულება (1.42) იღებს ფორმას
 ,
,
სად  - kth ჰარმონიკის ენერგია.
- kth ჰარმონიკის ენერგია.
სიგნალის ენერგია ამ შემთხვევაში
 ,
,
და მისი საშუალო სიმძლავრე
 .
.
ზემოაღნიშნული გამონათქვამებიდან გამომდინარეობს, რომ მათემატიკური სპექტრის k-ე სპექტრული კომპონენტის ენერგია ან საშუალო სიმძლავრე არის ფიზიკური სპექტრის შესაბამისი სპექტრული კომპონენტის ენერგიის ან სიმძლავრის ნახევარი. ეს გამოწვეულია იმით, რომ ფიზიკური სპექტრი თანაბრად ნაწილდება მათემატიკურ სპექტრს შორის.
| -τ და /2 |
| τ და /2 |
| თ |
| ტ |
| U 0 |
| S(t) |
დავალება No1 ჯგუფი RI – 210701
მართკუთხა იმპულსების პერიოდული თანმიმდევრობები ფართოდ გამოიყენება ელექტრონულ მოწყობილობებში სხვადასხვა აპლიკაციებისთვის. ამ შემთხვევაში, კავშირი პულსის ხანგრძლივობას τ და რხევის პერიოდს შორის თშეიძლება მნიშვნელოვნად განსხვავდებოდეს. მაგალითად, ვიბრაციები, რომლებიც წარმოქმნიან საათის გენერატორები, რომლებიც ადგენენ კომპიუტერის მუშაობის „ტემპს“, ხასიათდება τ და თდა რადარში გამოყენებული იმპულსები შეიძლება ასჯერ უფრო მოკლე იყოს ვიდრე პერიოდს. დამოკიდებულება თ/τ ეწოდება პულსის სამუშაო ციკლიდა შებრუნებული მნიშვნელობა (τ/ თ) - შევსების ფაქტორი.
ბრინჯი. 6.მართკუთხა იმპულსების თანმიმდევრობა (a) და ფურიეს რიგის კოეფიციენტები (b)
განვიხილოთ მართკუთხა პულსების თანმიმდევრობა ამპლიტუდით ა, ხანგრძლივობა τ და შემდგომი პერიოდით თ(ნახ. 6, ა). მოდით ავირჩიოთ დროის დათვლის დასაწყისი, როგორც ნაჩვენებია ფიგურაში, ანუ ისე, რომ პულსი იყოს სიმეტრიული ნულოვანი ნიშნის მიმართ და გამოვთვალოთ ფურიეს სერიის კოეფიციენტები (1). ფუნქციიდან გამომდინარე ს(ტ) ცულების ამ პოზიციით გამოდის თანაბარი, ყველა ბ ნტოლია ნულისა და ამისთვის ა ნჩვენ ვიღებთ:
ფურიეს სერია მართკუთხა იმპულსების თანმიმდევრობისთვის იღებს ფორმას:
 (6)
(6)
ფურიეს სერიის კოეფიციენტების მნიშვნელობები, გამოთვლილი ფორმულების გამოყენებით (5), გამოსახულია სპექტრულ დიაგრამაზე, რომელიც ნაჩვენებია ნახ. 6, ბ.
შანსები ა ნშეიძლება დაკავშირებული იყოს ფუნქციასთან  . მართლაც, ისინი პროპორციული იქნება (ფაქტორთან
. მართლაც, ისინი პროპორციული იქნება (ფაქტორთან  ) ფუნქციის მნიშვნელობები
) ფუნქციის მნიშვნელობები  ჰარმონიული სიხშირეების შესაბამისი არგუმენტებით. ეს ჩანს, თუ გამონათქვამი (5) გადაიწერება შემდეგნაირად:
ჰარმონიული სიხშირეების შესაბამისი არგუმენტებით. ეს ჩანს, თუ გამონათქვამი (5) გადაიწერება შემდეგნაირად:
 (7)
(7)
ასე რომ, ფუნქცია მოსწონს  არის კონვერტიკოეფიციენტებისთვის ფურიეს გაფართოებებიმართკუთხა იმპულსების თანმიმდევრობა (იხ. სურ. 6, ბ). კონვერტის ნულების მდებარეობა სიხშირის ღერძზე ვმდგომარეობიდან შეიძლება მოიძებნოს
არის კონვერტიკოეფიციენტებისთვის ფურიეს გაფართოებებიმართკუთხა იმპულსების თანმიმდევრობა (იხ. სურ. 6, ბ). კონვერტის ნულების მდებარეობა სიხშირის ღერძზე ვმდგომარეობიდან შეიძლება მოიძებნოს  ან
ან  , სად. პირველად კონვერტი მიდის ნულამდე სიხშირით ვ= 1/τ (ან ω = 2π/τ). შემდეგი, კონვერტის ნულები მეორდება ვ= 2/τ, 3/τ და ა.შ. ეს სიხშირეები შეიძლება ემთხვეოდეს (მთლიანი სამუშაო ციკლებს) ნებისმიერი სპექტრის ჰარმონიკის სიხშირეს და ფურიეს სერიიდან ეს სიხშირის კომპონენტები გაქრება. თუ მოვალეობის ციკლი არის მთელი რიცხვი, პერიოდი თზუსტად პულსის ხანგრძლივობის ჯერადი. შემდეგ კონვერტის ორ ნულს შორის იქნება სპექტრის ჰარმონიები ოდენობით ქ-
1.
, სად. პირველად კონვერტი მიდის ნულამდე სიხშირით ვ= 1/τ (ან ω = 2π/τ). შემდეგი, კონვერტის ნულები მეორდება ვ= 2/τ, 3/τ და ა.შ. ეს სიხშირეები შეიძლება ემთხვეოდეს (მთლიანი სამუშაო ციკლებს) ნებისმიერი სპექტრის ჰარმონიკის სიხშირეს და ფურიეს სერიიდან ეს სიხშირის კომპონენტები გაქრება. თუ მოვალეობის ციკლი არის მთელი რიცხვი, პერიოდი თზუსტად პულსის ხანგრძლივობის ჯერადი. შემდეგ კონვერტის ორ ნულს შორის იქნება სპექტრის ჰარმონიები ოდენობით ქ-
1.
ცხრილი 1 გვიჩვენებს, თუ როგორ არის დაკავშირებული პულსის პარამეტრები დროისა და სიხშირის წარმოდგენაში. 2. პერიოდის მატებასთან ერთად თსპექტრულ დიაგრამაზე ჰარმონიები უახლოვდება ერთმანეთს (სპექტრი ხდება "სქელი"). თუმცა, მხოლოდ პერიოდის შეცვლა არ ცვლის ამპლიტუდის სპექტრის გარსის ფორმას. კონვერტის ევოლუცია (მისი ნულების ცვლა) დამოკიდებულია პულსის ხანგრძლივობაზე. აქ ნაჩვენებია ამპლიტუდის სპექტრული დიაგრამების ევოლუცია მართკუთხა იმპულსების თანმიმდევრობებისთვის, რომელთა პულსის ხანგრძლივობა და პერიოდები განსხვავდება. სპექტრული დიაგრამების ორდინატთა ღერძები აჩვენებს ჰარმონიული ამპლიტუდების ფარდობით მნიშვნელობებს:  ისინი გამოითვლება ფორმულების გამოყენებით:
ისინი გამოითვლება ფორმულების გამოყენებით:
 (8)
(8)
ცხრილი 2.მართკუთხა იმპულსების მიმდევრობის ოსცილოგრამები და სპექტროგრამები

2.5. ქაოტური (ხმაური) რხევების სპექტრები
ქაოტური რხევა ს(ტ) - ეს შემთხვევითი პროცესი. მისი ყოველი განხორციელება მუდმივ პირობებში არ მეორდება და უნიკალურია. ელექტრონიკაში ქაოტურ რხევებს უკავშირდება ხმაური- დენების და ძაბვების რყევები, რომლებიც შემთხვევით იცვლება მუხტის მატარებლების შემთხვევითი მოძრაობის გამო. ამ კონტექსტში ქაოტური და ხმაურის ვიბრაცია სინონიმად ითვლება.
ბრინჯი. 7. საშუალო კვადრატული ხმაურის ძაბვის გაზომვის ბლოკ-სქემა
ხმაურის მერყეობაშეიძლება აღწერილი იყოს სიხშირის წარმოდგენით: ის ასოცირდება გარკვეულ სპექტრულ მახასიათებელთან, ხოლო შემთხვევითი პროცესისთვის ის უწყვეტია. წარმოდგენილია ქაოტური რხევების სპექტრული დაშლის თეორიული საფუძვლები. მკაცრ თეორიაში ჩაძირვის გარეშე, ჩვენ განვმარტავთ სტატისტიკური პარამეტრების ექსპერიმენტული კვლევის მეთოდოლოგიას ხმაურის ძაბვა ს(ტ) ნახატზე ნაჩვენები სქემის მიხედვით. 8.
რ  არის. 8.ხმაურის ძაბვის ინტენსივობის სპექტრული სიმკვრივის საზომი წრე
არის. 8.ხმაურის ძაბვის ინტენსივობის სპექტრული სიმკვრივის საზომი წრე
მოდით გამოვტოვოთ ხმაურის ძაბვა ს(ტ) ფილტრის მეშვეობით, რომელიც გამოყოფს რხევის ენერგიას ვიწრო ზოლში  სიხშირის მახლობლად ვ. თუ პირობა დაკმაყოფილებულია
სიხშირის მახლობლად ვ. თუ პირობა დაკმაყოფილებულია  <<
ვფილტრის გამოსავალზე რხევა დაემსგავსება სინუსოიდს სიხშირით ვ. თუმცა, ამ სინუსოიდის ამპლიტუდა და ფაზა ექვემდებარება ქაოტურ ცვლილებებს. ფილტრის გამტარუნარიანობის შემცირებით
<<
ვფილტრის გამოსავალზე რხევა დაემსგავსება სინუსოიდს სიხშირით ვ. თუმცა, ამ სინუსოიდის ამპლიტუდა და ფაზა ექვემდებარება ქაოტურ ცვლილებებს. ფილტრის გამტარუნარიანობის შემცირებით  გამომავალი რხევის ფორმა სულ უფრო უახლოვდება სინუსოიდს. მისი ამპლიტუდა მცირდება, მაგრამ ფილტრში გამავალი საშუალო კვადრატული ძაბვის თანაფარდობა (
გამომავალი რხევის ფორმა სულ უფრო უახლოვდება სინუსოიდს. მისი ამპლიტუდა მცირდება, მაგრამ ფილტრში გამავალი საშუალო კვადრატული ძაბვის თანაფარდობა (  ), გამტარუნარიანობამდე
), გამტარუნარიანობამდე  რჩება სასრული და, ზოლის თანმიმდევრული კლებით, მიდრეკილია გარკვეულ ზღვარზე ვ(ვ):
რჩება სასრული და, ზოლის თანმიმდევრული კლებით, მიდრეკილია გარკვეულ ზღვარზე ვ(ვ):
ზღვრული ღირებულება ვ(ვ) უწოდებენ სპექტრული ინტენსივობის სიმკვრივეპროცესი ს(ტ).
იგი უდრის ჰარმონიული კომპონენტების საშუალო ინტენსივობას სიხშირის ღერძის ერთეულ ინტერვალზე. გაზომვისას ვ(ვ) გამოიყენეთ ვიწრო ზოლიანი რეგულირებადი ფილტრი, რომელიც შეიძლება დარეგულირდეს ნებისმიერ სიხშირეზე მოცემულ გაზომვის დიაპაზონში. ფილტრში გამავალი ხმაურის ძაბვა ექვემდებარება კვადრატულ გამოვლენას და საშუალოდ (ინტეგრირებულია). შედეგი არის საშუალო კვადრატი:  . შემდგომ ცნობილი ფილტრის ზოლის გასწვრივ
. შემდგომ ცნობილი ფილტრის ზოლის გასწვრივ  გამოთვალეთ ვ(ვ).
პროცესის სრული ინტენსივობა- საშუალო კვადრატი
გამოთვალეთ ვ(ვ).
პროცესის სრული ინტენსივობა- საშუალო კვადრატი  - ნაპოვნია ხმაურის სპექტრული კომპონენტების ყველა სიხშირეზე ინტეგრაციით:
- ნაპოვნია ხმაურის სპექტრული კომპონენტების ყველა სიხშირეზე ინტეგრაციით:
 (10)
(10)
სამუშაოსთვის მოსამზადებლად, თქვენ უნდა შეისწავლოთ ეს სახელმძღვანელო სრულად. უფრო დეტალური ინფორმაცია ლაბორატორიული სამუშაოს თემაზე შეგიძლიათ იხილოთ წიგნის „ელექტრული ვიბრაციების სიხშირის სპექტრები, სპექტრული ანალიზი“ თავში.
მართკუთხა ვიდეო იმპულსების პერიოდული თანმიმდევრობა არის მოდულაციური ფუნქცია მართკუთხა რადიო იმპულსების (PPRP) პერიოდული თანმიმდევრობის ფორმირებისთვის, რომლებიც წარმოადგენს სიგნალებს მოძრავი სამიზნეების კოორდინატების აღმოსაჩენად და გასაზომად. ამრიგად, მოდულატორული ფუნქციის სპექტრის (PPVI) გამოყენებით, შესაძლებელია ზონდირებადი სიგნალის (PPVI) სპექტრის დადგენა შედარებით მარტივად და სწრაფად. როდესაც საცდელი სიგნალი აისახება მოძრავი სამიზნედან, იცვლება მატარებლის ვიბრაციის ჰარმონიული სპექტრის სიხშირეები (დოპლერის ეფექტი). შედეგად, შესაძლებელია მოძრავი სამიზნედან ასახული სასარგებლო სიგნალის იდენტიფიცირება სტაციონარული ობიექტებიდან (ადგილობრივი ობიექტები) ან ნელა მოძრავი ობიექტებიდან (მეტეოროლოგიური წარმონაქმნები, ფრინველთა ფარა და ა.შ.) არეკლილი (ჩარევა) ვიბრაციების ფონზე. .
PPPVI (ნახ. 1.42) არის ერთჯერადი მართკუთხა ვიდეო პულსების ერთობლიობა, რომლებიც მიჰყვება ერთმანეთს დროის თანაბარი ინტერვალებით. სიგნალის ანალიტიკური გამოხატულება.
სად არის პულსის ამპლიტუდა; - პულსის ხანგრძლივობა; - პულსის გამეორების პერიოდი; - პულსის გამეორების სიხშირე; - ექსპლუატაციის პერიოდი.
იმპულსების პერიოდული მიმდევრობის სპექტრული შემადგენლობის გამოსათვლელად გამოიყენება ფურიეს სერია. ერთჯერადი იმპულსების ცნობილი სპექტრებით, რომლებიც ქმნიან პერიოდულ მიმდევრობას, ჩვენ შეგვიძლია გამოვიყენოთ კავშირი იმპულსების სპექტრულ სიმკვრივესა და სერიის კომპლექსურ ამპლიტუდებს შორის:
ერთი მართკუთხა ვიდეო პულსისთვის, სპექტრული სიმკვრივე აღწერილია ფორმულით
ერთი პულსის სპექტრულ სიმკვრივესა და რიგის კომპლექსურ ამპლიტუდებს შორის კავშირის გამოყენებით, ჩვენ ვხვდებით
სადაც = 0; ± 1; ± 2; ...
ამპლიტუდა-სიხშირის სპექტრი (ნახ. 1.43) წარმოდგენილი იქნება კომპონენტების სიმრავლით:
ამ შემთხვევაში, დადებითი მნიშვნელობები შეესაბამება ნულოვან საწყის ფაზებს, ხოლო უარყოფითი მნიშვნელობები შეესაბამება საწყის ფაზებს ტოლი .
ამრიგად, PPPVI-ის ანალიტიკური გამოხატულება ტოლი იქნება
1.43-ზე ნაჩვენები გრაფიკების ანალიზიდან გამომდინარეობს:
· PPPVI სპექტრი არის დისკრეტული, შედგება ინდივიდუალური ჰარმონიებისგან სიხშირით.
· ASF-ის კონვერტი იცვლება კანონის შესაბამისად.
· კონვერტის მაქსიმალური მნიშვნელობა at უდრის მუდმივი კომპონენტის მნიშვნელობას.
· კენტი წილების შიგნით ჰარმონიის საწყისი ფაზები ტოლია 0-ის, ლუწი წილებში.
· თითოეული წილის შიგნით ჰარმონიის რაოდენობა უდრის.
სიგნალის სპექტრის სიგანე სიგნალის ენერგიის 90%-ზე
· სიგნალის ბაზა, ამიტომ სიგნალი მარტივია.
თუ შეცვლით იმპულსების ხანგრძლივობას ან მათი განმეორების სიხშირეს ფ(პერიოდი), შემდეგ შეიცვლება სპექტრის პარამეტრები და მისი ASF.
სურათი 1.43 გვიჩვენებს სიგნალის და მისი ASF ცვლილების მაგალითს, როდესაც პულსის ხანგრძლივობა გაორმაგებულია.
მართკუთხა ვიდეო პულსების პერიოდული თანმიმდევრობა და მათი ASF პარამეტრები, თ,. და თ, ნაჩვენებია სურათზე 1.44.
მოცემული გრაფიკების ანალიზიდან გამომდინარეობს:
1. PPPVI-სთვის პულსის ხანგრძლივობით:
· მოვალეობის კოეფიციენტი ქ=4, შესაბამისად, 3 ჰარმონია კონცენტრირებულია თითოეულ წილში;
· k-th ჰარმონიკის სიხშირე;
· სიგნალის სპექტრის სიგანე 90% ენერგიის დონეზე;
მუდმივი კომპონენტი უდრის
2. PPPVI-სთვის პულსის ხანგრძლივობით:
· მოვალეობის კოეფიციენტი q= 2, შესაბამისად, თითოეულ წილში არის 1 ჰარმონია;
· k-th ჰარმონიკის სიხშირე უცვლელი რჩება;
· სიგნალის სპექტრის სიგანე მისი ენერგიის 90%-ის დონეზე 2-ჯერ შემცირდა;
· მუდმივი კომპონენტი გაიზარდა 2-ჯერ.
ამრიგად, შეგვიძლია დავასკვნათ, რომ პულსის ხანგრძლივობის გაზრდით, ASF "შეკუმშულია" ორდინატთა ღერძის გასწვრივ (სიგნალის სპექტრის სიგანე მცირდება), ხოლო სპექტრული კომპონენტების ამპლიტუდები იზრდება. ჰარმონიული სიხშირეები არ იცვლება.
სურათზე 1.44. წარმოდგენილია სიგნალის და მისი ASF-ის ცვლილების მაგალითი გამეორების პერიოდის 4-ჯერ გაზრდით (განმეორების სიჩქარის 4-ჯერ შემცირება).
გ) სიგნალის სპექტრის სიგანე მისი ენერგიის 90%-ის დონეზე არ შეცვლილა;
დ) მუდმივი კომპონენტი შემცირდა 4-ჯერ.
ამრიგად, შეგვიძლია დავასკვნათ, რომ გამეორების პერიოდის მატებასთან ერთად (განმეორების სიხშირის დაქვეითება), "შეკუმშვა" ხდება ASF-ში სიხშირის ღერძის გასწვრივ (ჰარმონიკის ამპლიტუდები მცირდება მათი რიცხვის მატებასთან ერთად თითოეულ ლობში) . სიგნალის სპექტრის სიგანე არ იცვლება. გამეორების სიხშირის შემდგომი შემცირება (განმეორების პერიოდის მატება) გამოიწვევს (at) ჰარმონიების ამპლიტუდების შემცირებას უსასრულო მნიშვნელობებამდე. ამ შემთხვევაში, სიგნალი გადაიქცევა ერთად და შესაბამისად სპექტრი გახდება უწყვეტი.
დროის ფუნქციების სპექტრული წარმოდგენა ფართოდ გამოიყენება კომუნიკაციის თეორიაში. ელექტრული სქემების მახასიათებლებისა და საკომუნიკაციო არხებით შეტყობინებების გადაცემის თეორიული და ექსპერიმენტული შესწავლისთვის გამოიყენება სხვადასხვა ტიპის სიგნალები: ჰარმონიული რხევები, მუდმივი ძაბვის დონეები, მართკუთხა და რადიო პულსების თანმიმდევრობა და ა.შ. გამოთვლითი სიგნალები ერთეული ფუნქცია განსაკუთრებით მნიშვნელოვან როლს ასრულებს ელექტრული სქემების და იმპულსური ფუნქციის თეორიულ კვლევებში (დირაკის ფუნქცია). მოდით განვსაზღვროთ ყველაზე გავრცელებული ტიპიური სიგნალების სპექტრები.
11.1 მართკუთხა იმპულსების მიმდევრობის სპექტრი
იყოს მართკუთხა იმპულსების პერიოდული თანმიმდევრობა T პერიოდით, პულსის ხანგრძლივობით t და A ამპლიტუდით. სეგმენტზე პულსის აღწერის ფუნქციის ანალიტიკურ გამოხატულებას აქვს ფორმა.
 (11.1)
(11.1)
პერიოდული პულსის მიმდევრობის გრაფიკი ნაჩვენებია სურათზე 11.1.

სურათი 11.1
ეს ფუნქცია ლუწია, რადგან მისი გრაფიკი სიმეტრიულია ორდინატთან. შემდეგ ამ ფუნქციების ფურიეს კოეფიციენტები გამოითვლება ფორმულების გამოყენებით (KFT2), სადაც .

რიცხვი წარმოადგენს ფუნქციის საშუალო მნიშვნელობას პერიოდის განმავლობაში და მას მუდმივი კომპონენტი ეწოდება. სიხშირეს ეწოდება ფუნდამენტური, ანუ პირველი ჰარმონია, ხოლო k სიხშირეებს - უმაღლესი ჰარმონიები, სადაც k = 2,3,4,...
მოდით ავაშენოთ მართკუთხა იმპულსების განხილული მიმდევრობის ამპლიტუდის სპექტრი. ვინაიდან ფუნქცია პერიოდულია, მისი ამპლიტუდის სპექტრი გაფორმებულია. მოდი ავღნიშნოთ ნებისმიერი მიმდებარე ჰარმონიას შორის მანძილით. ცხადია, ის უდრის. kth ჰარმონიკის ამპლიტუდას (11.2) აქვს ფორმა
 (11.3)
(11.3)
ვიპოვოთ ურთიერთობა T პერიოდსა და პულსის ხანგრძლივობას შორის, რომლის დროსაც kth ჰარმონიკის ამპლიტუდა ნულდება.
A 2 ≈32V, A 3 ≈15V, A 4 ≈0, A 5 ≈6.36V, A 6 ≈10.5V, A 7 ≈6.36V, A 8 ≈0, A 9 ≈4.95V, A .7≈ 10.
გაანგარიშების შედეგად მიღებული ამპლიტუდის სპექტრი ნაჩვენებია სურათზე 11.2.

სურათი 11.2
ასეთ სპექტრს უწოდებენ ხაზს ან დისკრეტულ სპექტრს.
სპექტრები q=8 და q=16 გამოთვლილი და გამოსახულია ანალოგიურად. ისინი ნაჩვენებია სურათებში 11.3 და 11.4, შესაბამისად.

სურათი 11.3

სურათი 11.4
ნახატიდან ჩანს, რომ რაც უფრო დიდია მართკუთხა იმპულსების მუშაობის ციკლი, მით უფრო მცირეა პირველი ჰარმონიის ამპლიტუდა, მაგრამ უფრო ნელა მცირდება სპექტრი.
11.2 ერთი მართკუთხა პულსის სპექტრი
განვიხილოთ Ф (11.1) იმ შემთხვევისთვის, როდესაც T→∞, ანუ იმპულსების პერიოდული თანმიმდევრობა გადაგვარდება t u ხანგრძლივობის ერთ მართკუთხა პულსად.
ამ იმპულსის ანალიტიკური გამოხატულება დაიწერება შემდეგნაირად:
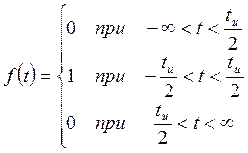
ამ ფუნქციის გრაფიკი ნაჩვენებია სურათზე 11.5.

სურათი 11.5
ამ შემთხვევაში, პირველი ჰარმონიის სიხშირე და ჰარმონიებს შორის მანძილი ხდება 0-ის ტოლი, შესაბამისად, სპექტრი გარდაიქმნება დისკრეტულიდან უწყვეტამდე, რომელიც შედგება უსასრულოდ დიდი რაოდენობის სპექტრული ხაზებისგან, რომლებიც მდებარეობს ერთმანეთისგან უსასრულოდ მცირე მანძილზე. ასეთ სპექტრს უწყვეტი ეწოდება. ეს იწვევს ყველაზე მნიშვნელოვან წესს: პერიოდული სიგნალები წარმოქმნის დისკრეტულ სპექტრებს, ხოლო არაპერიოდული სიგნალები წარმოქმნის უწყვეტ სპექტრებს.
მართკუთხა ერთჯერადი პულსის სპექტრი შეგიძლიათ იხილოთ უშუალოდ ფურიეს ტრანსფორმაციიდან (10.1)
